Reset password New user? Sign up
Existing user? Log in

Dynamic Programming
Already have an account? Log in here.
- Karleigh Moore
- Norbert Madarász
Dynamic programming refers to a problem-solving approach, in which we precompute and store simpler, similar subproblems, in order to build up the solution to a complex problem. It is similar to recursion , in which calculating the base cases allows us to inductively determine the final value. This bottom-up approach works well when the new value depends only on previously calculated values.
An important property of a problem that is being solved through dynamic programming is that it should have overlapping subproblems. This is what distinguishes DP from divide and conquer in which storing the simpler values isn't necessary.
To show how powerful the technique can be, here are some of the most famous problems commonly approached through dynamic programming:
- Backpack Problem : Given a set of treasures with known values and weights, which of them should you pick to maximize your profit whilst not damaging your backpack which has a fixed capacity?
- Egg Dropping : What is the best way to drop \(n\) eggs from an \(m\)-floored building to figure out the lowest height from which the eggs when dropped crack?
- Longest Common Subsequence : Given two sequences, which is the longest subsequence common to both of them?
- Subset Sum Problem : Given a set and a value \(n,\) is there a subset the sum of whose elements is \(n?\)
- Fibonacci Numbers : Is there a better way to compute Fibonacci numbers than plain recursion?
In a contest environment, dynamic programming almost always comes up (and often in a surprising way, no matter how familiar the contestant is with it).
Motivational Example: Change of Coins
Recursion with memoization, bidimensional dynamic programming: example, example: maximum paths.
What is the minimum number of coins of values \(v_1,v_2, v_3, \ldots, v_n\) required to amount a total of \(V?\) You may use a denomination more than once.
Optimal Substructure
The most important aspect of this problem that encourages us to solve this through dynamic programming is that it can be simplified to smaller subproblems.
Let \(f(N)\) represent the minimum number of coins required for a value of \(N\).
Visualize \(f(N)\) as a stack of coins. What is the coin at the top of the stack? It could be any of \(v_1,v_2, v_3, \ldots, v_n\). In case it were \(v_1\), the rest of the stack would amount to \(N-v_1;\) or if it were \(v_2\), the rest of the stack would amount to \(N-v_2\), and so on.
How do we decide which is it? Sure enough, we do not know yet. We need to see which of them minimizes the number of coins required.
Going by the above argument, we could state the problem as follows:
\[f(V) = \min \Big( \big\{ 1 + f(V - v_1), 1 + f(V-v_2), \ldots, 1 + f(V-v_n) \big \} \Big). \]
Because the coin at the top of the stack also counts as one coin, and then we can look at the rest.
Overlapping Subproblems
It is easy to see that the subproblems could be overlapping.
For example, if we are trying to make a stack of $11 using $1, $2, and $5, our look-up pattern would be like this: \[\begin{align} f(11) &= \min \Big( \big\{ 1+f(10),\ 1+ f(9),\ 1 + f(6) \big\} \Big) \\ &= \min \Big ( \big \{ 1+ \min {\small \left ( \{ 1 + f(9), 1+ f(8), 1+ f(5) \} \right )},\ 1+ f(9),\ 1 + f(6) \big \} \Big ). \end{align} \] Clearly enough, we'll need to use the value of \(f(9)\) several times.
One of the most important aspects of optimizing our algorithms is that we do not recompute these values. To do this, we compute and store all the values of \(f\) from 1 onwards for potential future use.
The recursion has to bottom out somewhere, in other words, at a known value from which it can start.
For this problem, we need to take care of two things:
Zero : It is clear enough that \(f(0) = 0\) since we do not require any coins at all to make a stack amounting to 0.
Negative and Unreachable Values : One way of dealing with such values is to mark them with a sentinel value so that our code deals with them in a special way. A good choice of a sentinel is \(\infty\), since the minimum value between a reachable value and \(\infty\) could never be infinity.
The Algorithm
Let's sum up the ideas and see how we could implement this as an actual algorithm:
| def coinsChange(V,v): dpTable = [float("inf")]*(V+1) dpTable[0] = 0 for i in xrange(1,V+1): for vi in v: if (i - vi) >= 0: dpTable[i] = min(dpTable[i],1+dpTable[i-vi]) return dpTable[V] |
We have claimed that naive recursion is a bad way to solve problems with overlapping subproblems. Why is that? Mainly because of all the recomputations involved.
Another way to avoid this problem is to compute the data first time and store it as we go, in a top-down fashion.
Let's look at how one could potentially solve the previous coin change problem in the memoization way. 1 2 3 4 5 6 7 8 9 10 11 12 def coinsChange ( V , v ): memo = {} def Change ( V ): if V in memo : return memo [ V ] if V == 0 : return 0 if V < 0 : return float ( "inf" ) memo [ V ] = min ([ 1 + Change ( V - vi ) for vi in v ]) return memo [ V ] return Change ( V )
Dynamic Programming vs Recursion with Caching
| \(\hspace{20mm}\) | |
| Faster if many sub-problems are visited as there is no overhead from recursive calls | \(\hspace{20mm}\) Intuitive approach |
| The complexity of the program is easier to see | \(\hspace{20mm}\) Computes only those subproblems which are necessary |
There are \(k\) types of brackets each with its own opening bracket and closing bracket. We assume that the first pair is denoted by the numbers 1 and \(k+1,\) the second by 2 and \(k+2,\) and so on. Thus the opening brackets are denoted by \(1, 2, \ldots, k,\) and the corresponding closing brackets are denoted by \(k+1, k+2, \ldots, 2k,\) respectively.
Some sequences with elements from \(1, 2, \ldots, 2k\) form well-bracketed sequences while others don't. A sequence is well-bracketed if we can match or pair up opening brackets of the same type in such a way that the following holds:
- Every bracket is paired up.
- In each matched pair, the opening bracket occurs before the closing bracket.
- For a matched pair, any other matched pair lies either completely between them or outside them.
In this problem, you are given a sequence of brackets of length \(N\): \(B[1], \ldots, B[N]\), where each \(B[i]\) is one of the brackets. You are also given an array of Values: \(V[1],\ldots, V[N] \).
Among all the subsequences in the Values array, such that the corresponding bracket subsequence in the B Array is a well-bracketed sequence, you need to find the maximum sum.
Task: Solve the above problem for this input.
Input Format
One line, which contains \((2\times N + 2)\) space separate integers. The first integer denotes \(N.\) The next integer is \(k.\) The next \(N\) integers are \(V[1],..., V[N].\) The last \(N\) integers are \(B[1],..., B[N].\)
Constraints
- \(1 \leq k \leq 7\)
- \(-10^6 \leq V[i] \leq 10^6\), for all \(i\)
- \(1 \leq B[i] \leq 2k\), for all \(i\)
Illustrated Examples
For the examples discussed here, let us assume that \(k = 2\). The sequence 1, 1, 3 is not well-bracketed as one of the two 1's cannot be paired. The sequence 3, 1, 3, 1 is not well-bracketed as there is no way to match the second 1 to a closing bracket occurring after it. The sequence 1, 2, 3, 4 is not well-bracketed as the matched pair 2, 4 is neither completely between the matched pair 1, 3 nor completely outside of it. That is, the matched pairs cannot overlap. The sequence 1, 2, 4, 3, 1, 3 is well-bracketed. We match the first 1 with the first 3, the 2 with the 4, and the second 1 with the second 3, satisfying all the 3 conditions. If you rewrite these sequences using [, {, ], } instead of 1, 2, 3, 4 respectively, this will be quite clear.
Suppose \(N = 6, k = 3,\) and the values of \(V\) and \(B\) are as follows: Then, the brackets in positions 1, 3 form a well-bracketed sequence (1, 4) and the sum of the values in these positions is 2 (4 + (-2) =2). The brackets in positions 1, 3, 4, 5 form a well-bracketed sequence (1, 4, 2, 5) and the sum of the values in these positions is 4. Finally, the brackets in positions 2, 4, 5, 6 form a well-bracketed sequence (3, 2, 5, 6) and the sum of the values in these positions is 13. The sum of the values in positions 1, 2, 5, 6 is 16 but the brackets in these positions (1, 3, 5, 6) do not form a well-bracketed sequence. You can check the best sum from positions whose brackets form a well-bracketed sequence is 13.
We'll try to solve this problem with the help of a dynamic program, in which the state , or the parameters that describe the problem, consist of two variables.
First, we set up a two-dimensional array dp[start][end] where each entry solves the indicated problem for the part of the sequence between start and end inclusive.
We'll try to think what happens when we run across a new end value, and need to solve the new problem in terms of the previously solved subproblems. Here are all the possibilities:
- When end <= start , there are no valid subsequences.
- When b[end] <= k , i.e, the last entry is an open bracket, no valid subsequence can end with it. Effectively, the result is the same if we hadn't included the last entry at all.
- When b[end] > k , i.e, the last entry is a closing bracket, one has to find the best match for it, or simply ignore it, whichever maximizes the sum.
Can you use these ideas to solve the problem?
Very often, dynamic programming helps solve problems that ask us to find the most profitable (or least costly) path in an implicit graph setting. Let us try to illustrate this with an example.
You are supposed to start at the top of a number triangle and chose your passage all the way down by selecting between the numbers below you to the immediate left or right. Your goal is to maximize the sum of the elements lying in your path. For example, in the triangle below, the red path maximizes the sum.
To see the optimal substructures and the overlapping subproblems , notice that everytime we make a move from the top to the bottom right or the bottom left, we are still left with smaller number triangle, much like this:
We could break each of the sub-problems in a similar way until we reach an edge-case at the bottom:
In this case, the solution is a + max(b,c) .
A bottom-up dynamic programming solution is to allocate a number triangle that stores the maximum reachable sum if we were to start from that position . It is easy to compute the number triangles from the bottom row onward using the fact that the
\[\text{best from this point} = \text{this point} + \max(\text{best from the left, best from the right}).\]
Let me demonstrate this principle through the iterations. Iteration 1: 1 8 5 9 3 Iteration 2: 1 2 10 13 15 8 5 9 3 Iteration 3: 1 2 3 20 19 10 13 15 8 5 9 3 Iteration 4: 1 2 3 4 23 20 19 10 13 15 8 5 9 3 So, the effective best we could do from the top is 23, which is our answer.
Problem Loading...
Note Loading...
Set Loading...
Dynamic Programming: Examples, Common Problems, and Solutions

Your changes have been saved
Email Is sent
Please verify your email address.
You’ve reached your account maximum for followed topics.
I've Covered iPhones for 11 Years: Here Are My 6 Favorites of All Time
I tried youtube's playables: here's why they're not worth your time, 8 apps that combine all your streaming services into one.
There’s no doubt that dynamic programming problems can be very intimidating in a coding interview. Even when you may know that a problem needs to be solved using a dynamic programming method, it’s a challenge to be able to come up with a working solution in a limited time frame.
The best way to be good at dynamic programming problems is to go through as many of them as you can. While you don’t necessarily need to memorize the solution to every problem, it’s good to have an idea of how to go about implementing one.
What Is Dynamic Programming?
Simply put, dynamic programming is an optimization method for recursive algorithms, most of which are used to solve computing or mathematical problems.
You can also call it an algorithmic technique for solving an optimization problem by breaking it into simpler sub-problems. A key principle that dynamic programming is based on is that the optimal solution to a problem depends on the solutions to its sub-problems.
Wherever we see a recursive solution that has repeated calls for the same inputs, we can optimize it using dynamic programming. The idea is to simply store the results of subproblems so that we do not have to re-compute them when needed later.
Dynamically programmed solutions have a polynomial complexity which assures a much faster running time than other techniques like recursion or backtracking. In most cases, dynamic programming reduces time complexities, also known as big-O , from exponential to polynomial.
Now that you have a good idea of what dynamic programming is, it’s time to check out a few common problems and their solutions.
Dynamic Programming Problems
1. knapsack problem.
Problem Statement
Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight doesn’t exceed a given limit and the total value is as large as possible.
You’re given two integer arrays values[0..n-1] and weights[0..n-1] which represent values and weights associated with n items respectively. Also given is an integer W which represents the knapsack capacity.
Here we’re solving the 0/1 knapsack problem, which means that we can choose to either add an item or exclude it.
- Create a two-dimensional array with n+1 rows and w+1 columns. A row number n denotes the set of items from 1 to i , and a column number w denotes the maximum carrying capacity of the bag.
- The numeric value at [i][j] denotes the total value of items up till i in a bag that can carry a maximum weight of j.
- At every coordinate [i][j] in the array, pick the maximum value that we can obtain without item i , or the maximum value that we can obtain with item i ---whichever is larger.
- The maximum obtainable value by including item i is the sum of item i itself and the maximum value that can be obtained with the remaining capacity of the knapsack.
- Perform this step until you find the maximum value for the W th row.
2. Coin Change Problem
Suppose you’re given an array of numbers that represent the values of each coin. Given a specific amount, find the minimum number of coins that are needed to make that amount.

- Initialize an array of size n+1 , where n is the amount. Initialize the value of every index i in the array to be equal to the amount. This denotes the maximum number of coins (using coins of denomination 1) required to make up that amount.
- Since there is no denomination for 0, initialise the base case where array[0] = 0 .
- For every other index i , we compare the value in it (which is initially set to n+1 ) with the value array[i-k] +1 , where k is less than i . This essentially checks the entire array up till i-1 to find the minimum possible number of coins we can use.
- If the value at any array[i-k] + 1 is lesser than the existing value at array[i] , replace the value at array[i] with the one at array[i-k] +1 .
3. Fibonacci
The Fibonacci Series is a sequence of integers where the next integer in the series is the sum of the previous two.
It’s defined by the following recursive relation: F(0) = 0, F(n) = F(n-1) + F(n-2) , where F(n) is the nth term. In this problem, we have to generate all the numbers in a Fibonacci sequence up till a given nth term.
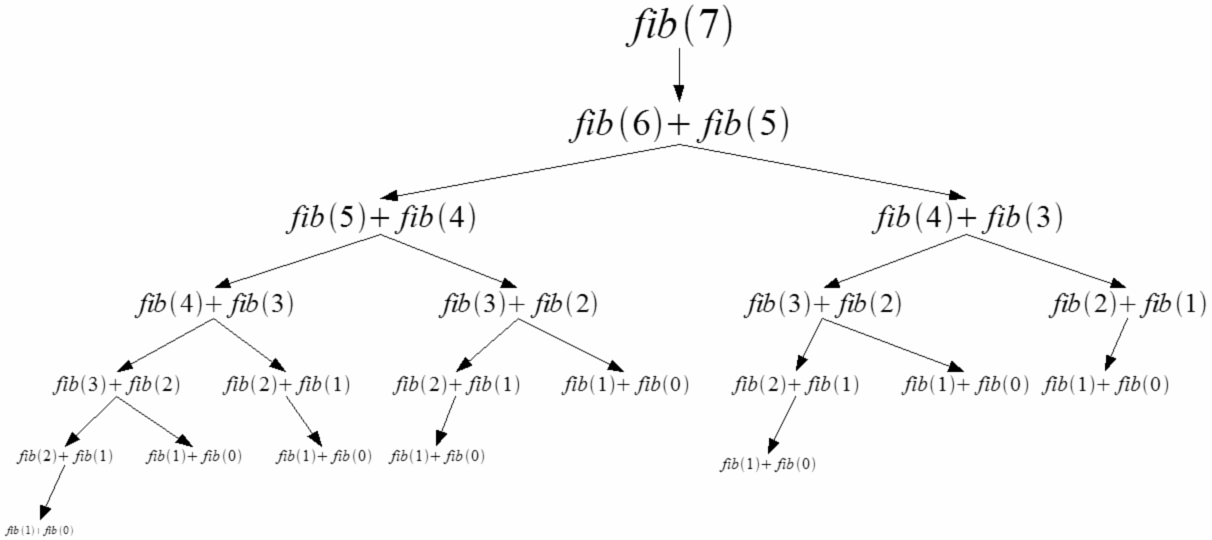
- First, use a recursive approach to implement the given recurrence relation.
- Recursively solving this problem entails breaking down F(n) into F(n-1) + F(n-2) , and then calling the function with F(n-1) and F(n+2) as parameters. We do this until the base cases where n = 0 , or n = 1 are reached.
- Now, we use a technique called memoization. Store the results of all function calls in an array. This will ensure that for every n, F(n) only needs to be calculated once.
- For any subsequent calculations, its value can simply be retrieved from the array in constant time.
4. Longest Increasing Subsequence
Find the length of the longest increasing subsequence inside a given array. The longest increasing subsequence is a subsequence within an array of numbers with an increasing order. The numbers within the subsequence have to be unique and in ascending order.
Also, the items of the sequence do not need to be consecutive.
- Start with a recursive approach where you calculate the value of the longest increasing subsequence of every possible subarray from index zero to index i, where i is lesser than or equal to the size of the array.
- To turn this method into a dynamic one, create an array to store the value for every subsequence. Initialise all the values of this array to 0.
- Every index i of this array corresponds to the length of the longest increasing subsequence for a subarray of size i .
- Now, for every recursive call of findLIS(arr, n) , check the n th index of the array. If this value is 0, then calculate the value using the method in the first step and store it at the n th index.
- Finally, return the maximum value from the array. This is the length of the longest increasing subsequence of a given size n .
Solutions to Dynamic Programming Problems
Now that you’ve gone through some of the most popular dynamic programming problems, it’s time to try implementing the solutions by yourself. If you’re stuck, you can always come back and refer to the algorithm section for each problem above.
Given how popular techniques such as recursion and dynamic programming are today, it won’t hurt to check out some popular platforms where you can learn such concepts and hone your coding skills . While you might not run into these problems on a daily basis, you'll surely encounter them in a technical interview.
Naturally, having the know-how of common problems is bound to pay dividends when you go for your next interview. So open up your favourite IDE , and get started!
- Programming
Dynamic Programming: Definition, Methods, and Practice Questions

Dynamic programming is a useful problem-solving technique that every developer should know. While the basics are easy to learn, dynamic programming can be difficult to master. In this post, we break down the fundamentals of dynamic programming and share challenge questions to start practicing.
What is Dynamic Programming?
Dynamic programming is a problem-solving paradigm used to find a solution by breaking the larger problem into subproblems. This approach takes advantage of the fact that the optimal solution to a problem depends upon the optimal solution to its subproblems.
But dynamic programming isn’t the right approach for every problem. You can use dynamic programming to solve a problem if that problem has two characteristics:
- Overlapping Subproblems: The problem can be divided into a number of subproblems of similar type but of smaller size than the original one.
- Optimal Substructure Property: The optimal solution to the problem can be formulated from the optimal solution to its subproblems.
Dynamic Programming vs Greedy Algorithms
One helpful way to understand dynamic programming is to compare it to greedy algorithms.
A greedy algorithm is a simple, intuitive algorithm that is used in optimization problems. The algorithm makes the optimal choice at each step to find the global or overall optimal solution to the entire problem.
However, a greedy algorithm isn’t always the right approach, as it can create an inaccurate or suboptimal solution. In some situations, the largest sum or most optimal path is “hiding behind the door” of an answer that at first appears small or suboptimal.
In contrast, dynamic programming can break those decisions into components and solve for the overall optimal solution. The drawback, however, is that dynamic programming can be challenging, compared to the easier greedy algorithms .
Dynamic Programming Methods
Dynamic Programming has two methods that can be used to solve problems: top-down and bottom-up.
Top-Down Approach
A top-down (recursive) approach tries to solve the bigger problem by recursively finding the solution to smaller problems while also storing local solutions in a look-up table such that those are not computed each time. This technique is called Memo-ization.
Memoization
The advantage of the top-down approach is that it’s more intuitive to come up with solutions than the other method. However, this doesn’t always produce the most optimal solution, as it often leads to code that is slower and lengthier.
F(n) = (F(n – 1) + F(n -3), if (n >=3)
F(n) = 7, otherwise
Given n, find the n th term of the recurrence.
Top-Down Solution
int F[MAXSIZE] ;
// set F to some unique value like -1 in this case.
int solve(int n){
if(n < 3){
return 7 ; // recurrence definition
int &ret = F[n] ; // cache technique
if(ret != -1) // absence of -1 indicate that this is already computed
return ret ; // use this computed result
ret = solve(n-3) + solve(n-1) ; // compute otherwise
return F[n] = ret ; // final return computed answer
Bottom-Up Approach
The bottom-up (iterative) approach is the opposite of the top-down approach in that you start from the smallest solution and go up to the required solution. The bottom-up approach tends to produce shorter, more optimal code. However, thinking of a bottom-up solution is less intuitive, and their base cases are often trickier than top-down base cases.
Bottom-Up Solution
F[0] = F[1] = F[2] = 7 ; // recurrence definition
for(int i=3;i<=n;i++)
F[i] = F[i-1] + F[i-3] ; // recurrence definition
return F[n] ;
Dynamic Programming Questions
Problem: row of numbers.
You have a row of numbers. In every turn, you can remove either the leftmost or the rightmost number and get points equal to turn_number x value of removed number. What is the maximum number of points you can get?
While you might think to use a greedy algorithm, that solution is not correct. [2, 3, 5, 1, 4] is a counter-example. This leads to the answer 2 x 1 + 3 x 2 + 4 x 3 + 1 x 4 + 5 x 5 = 49. The optimal answer in this case would be 2 x 1 + 4 x 2 + 1 x 3 + 3 x 4 + 5 x 5 = 50.
The correct solution is a dynamic programming approach.
Assume we have a function f(i, j) which gives us the optimal score of picking numbers with indices from i to j assuming the picking begins at turn number 1. Then, our answer would be f(1, n) where n is the total count of numbers.
However, notice that since we can only pick the leftmost one or the rightmost one, f(1, n) = max(g(2, n)) + val 1 , g(1, n – 1) + val j ) where g(i, j) is the optimal cost assuming picking begins at turn number 2.
A small observation: g(i, j) = f(i, j) + sum of all numbers from i to j.
Which means: f(i, j) = max(f(i, j – 1)) + sum(i, j – 1) + val j , f(i + 1, j) + sum(i + 1, j)
Computing this relation by recursion will take an exponential amount of time because the problem of size j – i gets reduced to two instances of problem sizes j – i -1 each.
This gives the recurrence:
T(n) = 2T(n – 1)
or, T(n) = O(2 n )
Let’s try to handle this.
First of all, notice that this problem has both the required properties of a dynamic programming problem. The answer depends on the answers to smaller subproblems.
These subproblems overlap with each other: f(i, j – 1) and f(i + 1, j) both call f(i + 1, j – 1).
However, there are only O(n 2 ) different parameters of f and, therefore, only O(n 2 ) different values of f.
So, we can use memoization while calculating f. Once it has been evaluated, all subsequent calls to this state are answered using the stored value.
The complexity of this solutions is: number of states x number of transitions from each state, which is O(n 2 ) for this problem.
It is important to note that every recursion must have a base case in order to terminate. The base case here is pretty simple: f(i, i) = val i : ∀i
Problem: Max Array Sum
Difficulty Level: Medium
Given an array of integers, find the subset of non-adjacent elements with the maximum sum. Calculate the sum of that subset. It is possible that the maximum sum is 0, the case when all elements are negative.
The following subsets with more than 1 element exist. These exclude the empty subset and single element subsets which are also valid.
Subset Sum
[-2, 3, 5] 6
[-2, 3] 1
[-2, -4] -6
[-2, 5] 3
[1, -4] -3
[1, 5] 6
[3, 5] 8
The maximum subset sum is 8. Note that any individual element is a subset as well.
arr = [-2, -3, -1]
In this case, it is best to choose no element:
Function Description
Complete the maxSubsetSum function in the editor below.
maxSubsetSum has the following parameter(s):
- int arr[n]: an array of integers
– int: the maximum subset sum
Input Format
The first line contains an integer, n.
The second line contains n space-separated integers arr[i].
Constraints
- 1 <= n <= 10 5
- -10 4 <= arr[i] <= 10 4
Sample Input
Sample Output
Explanation
Our subsets are [2, 5, 4]. [2, 5], [2,8], [2, 4], [1, 8], [1, 4] and [5, 4] The maximum subset sum is 11 from the first subset listed.
To solve the problem with dynamic programming, work through the array, keeping track of the max at each position until you get to the last value of the array. You should start with the base cases defined before iterating through the remainder of the array.
Challenge Problem: Billboards
Difficulty Level: Advanced
Below is an advanced-level dynamic programming problem that covers topics such as dynamic programming and priority queue. Only 36.09% of developers in the HackerRank Community that have attempted this problem have succeeded. Good luck!
ADZEN is a popular advertising firm in your city that owns all n billboard locations on Main Street. The city council passed a new zoning ordinance mandating that no more than k consecutive billboards may be up at any given time. For example, if there are n = 3 billboards on Main street and k = 1, ADZEN must remove either the middle billboard, the first two billboards, the last two billboards, or the first and last billboard.
Being a for-profit company, ADZEN wants to lose as little advertising revenue as possible when removing the billboards. They want to comply with the new ordinance in such a way that the remaining billboards maximize their total revenues (i.e., the sum of revenues generated by the billboards left standing on Main street).
Given n, k, and the revenue of each of the n billboards, find and print the maximum profit that ADZEN can earn while complying with the zoning ordinance. Assume that Main street is a straight, contiguous block of n billboards that can be removed but cannot be reordered in any way.
For example, if there are n = 7 billboards, and k = 3 is the maximum number of consecutive billboards that can be active, with revenues = [5, 6, 4, 2, 10, 8, 4], then the maximum revenue that can be generated is 37: 5 + 6 + 4 + 2 + 10 + 8 + 4.
Complete the billboards function in the editor below. It should return an integer that represents the maximum revenue that can be generated under the rules.
billboards has the following parameter(s):
- k: an integer that represents the longest contiguous group of billboards allowed
- revenue: an integer array where each element represents the revenue potential for a billboard at that index
The first line contains two space-separated integers, n (the number of billboards) and k (the maximum number of billboards that can stand together on any part of the road).
Each line i of the n subsequent lines contains an integer denoting the revenue value of billboard i (where 0 <= i <= n).
- 1 <= n < 10^ 5
- 1 <= k <=n
- 0 <= revenue value of any billboard <= 2 * 10^ 9
Output Format
Print a single integer denoting the maximum profit ADZEN can earn from Main street after complying with the city’s ordinance.
Sample Input 0
Sample Output 0
Explanation 0
There are n = 6 billboards, and we must remove some of them so that no more than k = 2 billboards are immediately next to one another.
We remove the first and fourth billboards, which gives us the configuration _ 2 3 _ 6 10 and a profit of 2 + 3 + 6 + 10 + 21. As no other configuration has a profit greater than 21, we print 21 as our answer.
Sample Input 1
Sample Output 1
Explanation 1
There are n = 5 billboards, and we must remove some of them so that no more than k = 4 billboards are immediately next to one another.
We remove the first billboard, which gives us the configuration _ 2 3 4 5 and a profit of 2 + 3 +4 + 5 = 14. As no other configuration has a profit greater than 14, we print 14 as our answer.
Basics of Dynamic Programming
Dynamic Programming Interview Questions
15 Common Problem-Solving Interview Questions
HackerRank Basic Problem-Solving Skills Certification
Get started with HackerRank
Over 2,500 companies and 40% of developers worldwide use HackerRank to hire tech talent and sharpen their skills.
Recommended topics
- Coding Questions
- Interview Preparation

6 REST API Interview Questions Every Developer Should Know
Dynamic Programming: An Approach to Solving Computing Problems
Dynamic programming is a useful way to efficiently solve certain types of problems you’ll encounter in computer science. This guide introduces you to the its basic principles and steps.
Sometimes in computer science, you will run into problems. You can divide these into subproblems, which can, in turn, be divided into smaller subproblems. If the smaller subproblems overlap, then you can save the result in memory for future reference. This way, you don’t need to compute the same result multiple times, thus increasing the efficiency of the program substantially. This way of solving these problems is referred to as dynamic programming.
In this article, you will learn what dynamic programming is. I will also show how to compute Fibonacci numbers, which is a simple problem that dynamic programming can solve. I will compare the dynamic programming solutions to the naive solution that uses recursion. These examples are written in Python syntax. Finally, I’ll also give some general pointers to keep in mind when attempting to solve problems using dynamic programming
Dynamic programming
More From Artturi Jalli: Python Cheat Sheet: A Handy Guide to Python
What Types of Problems Can Dynamic Programming Solve?
Dynamic programming is typically a way to optimize solutions to certain problems that use recursion. If a recursive solution to a problem has to compute solutions for subproblems with the same inputs repeatedly, then you can optimize it through dynamic programming. As mentioned earlier, in this case, you would simply save the result of the computation for use later if and when it’s needed. This optimization can reduce the time complexity of an algorithm from exponential time to polynomial time. This means that the number of computations n scales like a polynomial expression instead of scaling like an exponential expression as n increases. In general, polynomial expressions grow much slower than exponential expressions.
There are two conditions that need to be satisfied to use dynamic programming:
- Overlapping subproblems
- Optimal substructure property
What Are Overlapping Subproblems?
I alluded to the overlapping subproblems condition earlier. It simply means that when solving the problem in question, the solutions for the same subproblems are repeatedly necessary. In this case, the solutions to these subproblems can be stored for later use to skip recomputation.
Another way to think about this condition is to turn it upside down. If there are no overlapping subproblems, then there’s no point in saving the solutions for the subproblems, and you can’t use dynamic programming.
There are two different ways of storing the solutions to the overlapping subproblems:
- Memoization (top-down)
- Tabulation (bottom-up)
What Is Memoization?
The memoization approach to dynamic programming is very similar to the naive recursion approach, with only a small change. The difference is that we use a lookup table to store solutions to the subproblems, and then use this table to check whether that solution already exists.
If the solution for a certain subproblem already exists in the lookup table, then that solution is returned from the lookup table. If it does not, then it needs to be computed (through recursion) and added to the lookup table.
For the sake of clarity, let’s define a solution for a subproblem in our dynamic programming problem to be DP[X] ., with DP[N] being the desired solution and DP[0] being the base solution. In the memoization approach, the program starts from DP[N] and asks for the solutions from which DP[N] can be reached (these should be subproblems of lower order DP[n<N]) . Then, from these states, the same process is repeated recursively, until reaching the base solution DP[0] .
If this feels a little too abstract, don’t worry. The examples introduced later in this article should clarify what I mean.
Memoization is known as a top-down approach to dynamic programming since the program will start from the desired, last (top) state and work its way down recursively.
What Is Tabulation?
The tabulation approach to dynamic programming works in a reverse manner compared to the memoization approach. The program will start from the base (or bottom) solution for the subproblem and work its way up, solving the subproblems one by one until reaching the desired solution.
In terms of solutions to subproblems, the tabulation approach starts from the base solution DP[0] and then calculates DP[1], DP[2], … DP[N] until reaching the desired solution for the subproblem DP[N] . Since we started from the base solution DP[0] and worked towards the desired solution DP[N] , the tabulation approach is also known as a bottom-up approach.
Again, the examples below should make this easier to understand.
What Is Optimal Substructure Property?
If the optimal solution to a problem can be obtained using the optimal solution to its subproblems, then the problem is said to have optimal substructure property .
As an example, let’s consider the problem of finding the shortest path between ‘Start’ and ‘Goal’ nodes in the graph below. The nodes are connected to other nodes via edges, and the distance between two connected nodes is marked with a number next to the edge.
The shortest path from the Start node to the Goal node is through nodes three and four.
This problem clearly has optimal substructure property. Since the shortest path from the Start node to the Goal node goes through Node Four, it clearly follows that this path is a combination of the shortest path from the Start node to Node Four and the shortest path from Node Four to the Goal node.
Many problems do not have optimal substructure property. For example, the problem of finding the longest path (with no cycles) between the Start node and the Goal node in the above graph doesn’t. Here’s how you can see this:
The longest path is: Start - Node Three - Node Two - Node One - Node Four - Goal. However, this does not imply that the longest path from the Start node to Node Two is Start - Node Three - Node Two. The longest path from the Start node to Node Two is actually Start - Node One - Node Four - Node Three - Node Two (and Start - Node One - Node Four - Goal - Node Two, which has equal length to the first one).
Dynamic Programming Example: Calculating Fibonacci Numbers
One of the simplests examples of dynamic programming is the computation of Fibonacci numbers, which are numbers from the Fibonacci sequence. The first Fibonacci number is zero, the second is one, and the subsequent numbers are the sum of the previous two Fibonacci numbers. The 10 first Fibonacci numbers are zero, one, one, two, three, five, eight, 13, 21, and 34.
Let’s first start with the naive, recursive solution. Here’s a Python function to calculate the nth Fibonacci number (indexing starts from zero):
From this example it is easy to see that this problem satisfies the overlapping subproblems condition since the function clearly has to calculate the previous Fibonacci numbers multiple times (when n > three). The smallest Fibonacci numbers are computed most often, when this function is called for a large n.
This problem also clearly has optimal substructure since there is only a single solution for the subproblems, which are used to compute the solution to the desired problem.
Due to the recursion, this function runs in exponential time.
Let’s next look at how this could be solved using dynamic programming. Let’s start with a top-down solution using memoization. Here’s a Python function that calculates the nth Fibonacci number that implements dynamic programming through memoization:
This approach is quite similar to the recursive approach since it starts from calculating the nth Fibonacci number and, in order to calculate it, goes onto calculating the n-1st and n-2nd Fibonacci numbers. The difference is in the lookup table, where the smaller Fibonacci numbers will be saved as they are calculated, so that they do not need to be calculated again and again.
This makes this function actually run in linear time instead of exponential time.
For the sake of an example, let’s also look at a Python function that solves the same problem in a bottom-up manner with dynamic programming using tabulation:
In this solution, the nth Fibonacci number is calculated in a bottom-up manner, starting by calculating the first Fibonacci number, then the second, third and so on until reaching the nth Fibonacci number. This function also runs in linear time.
More in Software Engineering: Glob Module in Python: Explained
How to Solve Problems Using Dynamic Programming
The first step to solving a problem using dynamic programming is to identify it as a dynamic programming problem. If you can validate that the problem has overlapping subproblems and that it satisfies the optimal substructure property, you can be sure that you can solve it with dynamic programming.
The second step is to decide on a state expression. This state is the set of parameters that uniquely identifies the different subproblems.
In the Fibonacci numbers example, the parameter identifying the state would just be the serial number of a certain Fibonacci number.
There can be more than one parameter identifying a state. You should always use as few parameters as possible, however.
The third — and probably hardest — step in solving problems using dynamic programming is formulating the relation between the different states.
In the Fibonacci number case this is simple, however, since the nth Fibonacci number is the sum of the n-1st and n-2nd Fibonacci numbers. So F[n] = F[n-1] + F[n-2].
The fourth step is to implement memoization or tabulation for the states that you decided upon, using the relation you discovered between the states. This means simply saving the state (or in other words the solution to a certain subproblem) so it can be recovered from memory without recomputation when it is needed again. This should be fairly simple, if you did steps one to three well
Recent Software Engineering Perspectives Articles

Dynamic Programming 101 | Types, Examples, and Use-Cases
Say you're planning a road trip across the country. You've got a list of cities, but you can't decide on the best route. You want to complete the trip without wasting time driving back and forth. Here's how you could plan your trip in a better way:

Kishan Pandey
Dynamic programming is one of the finest ways to solve a class of problems with sub-problems. Did that sound difficult to understand? Dive in to learn all about it with clear concepts and examples.
Dynamic programming (often abbreviated as DP) is a method for solving complex problems by breaking them down into simpler, smaller, more manageable parts. The results are saved, and the subproblems are optimized to obtain the best solution. The results are saved, and the subproblems are optimized to obtain the best solution. That sounds similar to so many other things, right? Well, let's start with an example.
Let's say you're planning a road trip across the country. You've got a list of cities you want to visit, but you can't decide on the best route. You want to visit all the cities without wasting too much time driving back and forth.
Here's how you could plan your trip in a better way:
Break the problem into smaller subproblems: The subproblems in this case are the routes from one city to another. You need to determine the time or distance between each pair of cities.
Solve each subproblem and store the solution : You can use a mapping app to find the shortest route (in time or distance) between each pair of cities. You then store this information for later use.
Use the solutions of the subproblems to solve the original problem : Now, using the information you've gathered and stored, you can construct the shortest possible route that visits all the cities. You start from your home city and then go to the nearest city. From there, you go to the nearest city that you haven't visited yet, and so on.
This is just a simple example of how dynamic programming works, but it gives you an idea of the process: breaking a complex problem down into simpler parts, solving each part, storing the solutions, and then combining the solutions to solve the original problem.
Table of Contents:
What is dynamic programming
When to use dynamic programming
The fibonacci sequence
Step-by-step approach to DP
Types of dynamic programming
Which approach to choose when
What is Dynamic Programming
Thought first by Richard Bellman in the 1950s, Dynamic Programming (DP) is a problem-solving technique used in computer science and mathematics to solve complex larger problems by breaking them down into simpler, smaller overlapping subproblems. The key idea is solving each subproblem once and storing the results to avoid redundant calculations. DP is particularly useful for problems where the solution can be expressed recursively and the same subproblem appears multiple times.
It's like tackling a giant jigsaw puzzle by piecing together smaller sections first.
Simply put, DP stores the solution to each of these smaller parts to avoid doing the same work over and over again(like you would store the shortest routes between cities in the first example). So, with dynamic programming, you're not just working harder, you're working smarter!
When to use Dynamic Programming?
So, how do you know when to use dynamic programming? There are two key hallmarks of a problem that's ripe for a DP approach:
- Overlapping Subproblems: Dynamic Programming thrives on identifying and solving overlapping subproblems. These are smaller subproblems within a larger problem that are solved independently but repeatedly. By solving and storing the results of these subproblems, we avoid redundant work and speed up the overall solution. Let’s go back to the road trip example. Imagine that the travel from City A to City B is common in several different routes. Now, instead of calculating the distance between the two cities every single time we’re mapping different routes, we can store the distance and reuse it whenever needed. This is an example of overlapping subproblems.
- Optimal Substructure: Another crucial concept is the optimal substructure property. It means that the optimal solution to a larger problem can be generated from the optimal solutions of its smaller subproblems. This property allows us to break down complex problems into simpler ones and build the solution iteratively. Let's say we've figured out the shortest route from City A to City B, and the shortest route from City B to City C. The shortest route from City A to City C via City B would be the combination of these two shortest routes. So, by knowing the optimal solutions (shortest routes) to the subproblems, we can determine the optimal solution to the original problem. That's an optimal substructure.
Practical Application: The Fibonacci Sequence
To really get a grip on dynamic programming, let's explore a classic example: The Fibonacci sequence.
It is a series of numbers in which each number is the sum of the two preceding ones, usually starting with 0 and 1.
Fibonacci Series: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34…and so on.
Mathematically, we could write each term using the formula:
F(n) = F(n-1) + F(n-2),
With the base values F(0) = 0, and F(1) = 1. And we’ll follow the above relationship to calculate the other numbers. For example, F(6) is the sum of F(4) and F(5), which is equal to 8.
Let’s look at the diagram for better understanding.
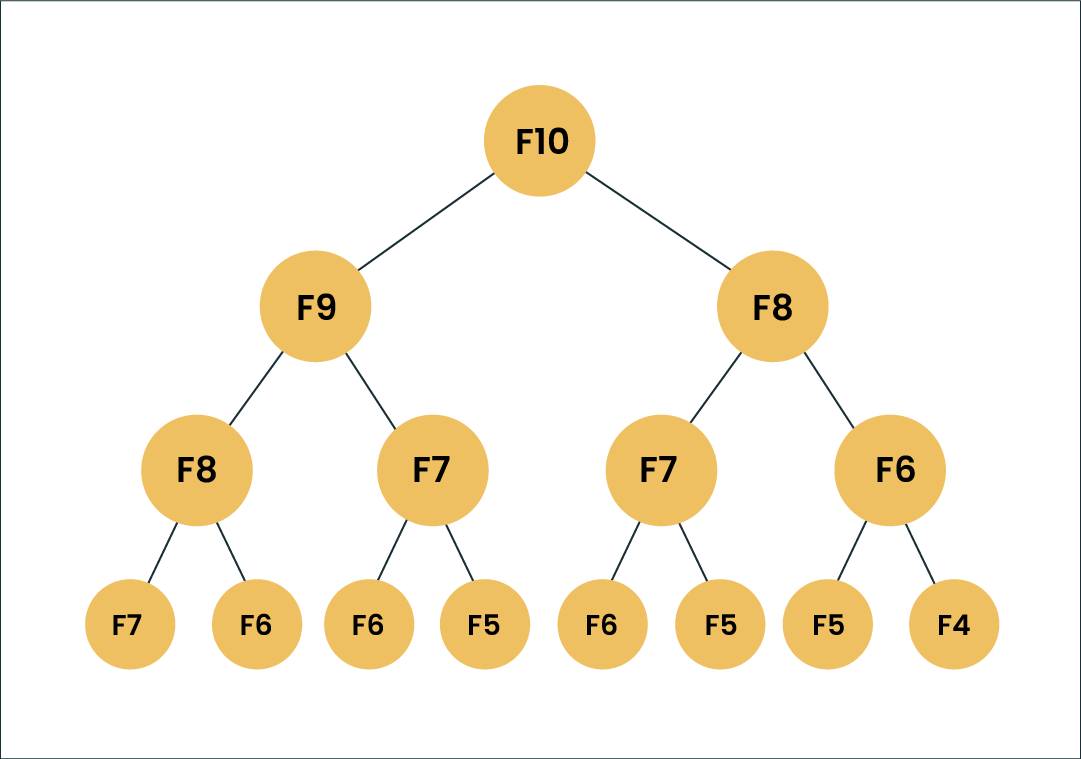
Suppose we’ve to calculate F(10). Going by the formula, F(10) should be the sum of F(8) and F(9). Similarly, F(9) would also be the sum of the subproblems F(7) and F(8). As you can see, F(8) is an overlapping subproblem here.
In the above example, if we calculate the F(8) in the right subtree, then it would result in a increased usage of resources and reduce the overall performance.
The better solution would be to store the results of the already computed subproblems in an array. First, we’ll solve F(6) and F(7) which will give us the solution to F(8) and we’ll store that solution in an array and so on. Now when we calculate F(9), we already have the solutions to F(7) and F(8) stored in an array and we can just reuse them. F(10) can be solved using the solutions of F(8) and F(9), both of which are already stored in an array.
Similarly, at each iteration we store the solutions so we don’t have to solve them again and again. This is the main attribute of dynamic programming.
If you try to compute this sequence with a straightforward recursive function, you'll end up doing a lot of unnecessary work. ( Want to understand recursion from scratch? )
Here's a simple Python implementation using DP to calculate a Fibonacci sequence:
Step-by-Step Approach to DP
Let's explore how to implement dynamic programming step-by-step:
- Grasp the Problem
- Find the Overlapping Subproblems
- Compute and Store Solutions
- Construct the Solution to the Main Problem
Types of Dynamic Programming
Dynamic programming is divided into two main approaches: top-down (memoization) and bottom-up (tabulation). Both of these methods help in solving complex problems more efficiently by storing and reusing solutions of overlapping subproblems, but they differ in the way they go about it.
Let's dive into these two approaches:
Top-Down DP (Memoization)
In the top-down approach, also known as memoization, we start with the original problem and break it down into subproblems. Think of it like starting at the top of a tree and working your way down to the leaves.
Here, problems are broken into smaller ones, and the answers are reused when needed. With every step, larger, more complex problems become tinier, less complicated, and, thus, faster to solve, and the results of each subproblem are stored in a data structure like a dictionary or array to avoid recalculating them. The ‘memoization’ (a key technique in DP where you store and retrieve previously computed values) process is equivalent to adding the recursion (any function that calls itself again and again) and caching steps.
Some parts can be reused for the same problem and solved when requested, making them easier to debug. However, this approach results in more memory in the call stack being occupied, which can result in a reduction in overall performance and stack overflow.
Let's revisit the Fibonacci sequence example:
Here, memo is a dictionary that stores the previously computed numbers. Before we compute a new Fibonacci number, we first check if it's already in memo. If it is, we just return the stored value. If it's not, we compute it, store it in memo, and then return it.
Bottom-Up DP (Tabulation)
The bottom-up approach, also known as tabulation, takes the opposite direction. This approach solves problems by breaking them up into smaller ones, solving the problem with the smallest mathematical value, and then working up to the problem with the biggest value. Solutions to its subproblems are compiled in a way that falls and loops back on itself. Users can opt to rewrite the problem by initially solving the smaller subproblems and then carrying those solutions for solving the larger subproblems.
Here, we fill up a table (hence the name "tabulation") in a manner that uses the previously filled values in the table. This way, by the time we come to the problem at hand, we already have the solutions to the subproblems we need.
Let's use the Fibonacci sequence again to illustrate the bottom-up approach:
In this case, fib_table is an array that stores the Fibonacci numbers in order. We start by filling in the first two numbers (0 and 1), and then we iteratively compute the rest from these initial numbers.
In contrast to the top-down approach, the bottom-up approach relies on eliminating recursion functions. There is no stack overflow, and memory space is saved with reduced timing complexity, making it more efficient and preferred when the order of solving subproblems is not critical.
Which approach to choose?
Both top-down and bottom-up dynamic programming can be useful, and your choice depends on the problem at hand and the specific requirements of your program.
The top-down approach might be easier to understand because it follows the natural logic of the problem, but it can involve a lot of recursion and may have a larger memory footprint due to the call stack.
On the other hand, the bottom-up approach can be more efficient because it avoids recursion and uses a loop instead, but it might require a better understanding of the problem to build the solution iteratively.
What are the signs of DP suitability?
Identifying whether a problem is suitable for solving with dynamic programming (DP) involves recognizing certain signs or characteristics that suggest DP could be an effective approach. Here are some common signs that indicate a problem might be a good fit for dynamic programming:
- Overlapping Subproblems: A problem that can be broken down into smaller subproblems that are solved independently, and the same subproblems encountered multiple times strongly indicates DP suitability.
- Optimal Substructure: Problems that exhibit optimal substructure can often be solved using DP. This means that the optimal solution for a larger problem can be constructed from the optimal solutions of its smaller subproblems.
- Recursive Nature: Problems that can be naturally expressed using recursion are often well-suited for DP.
- Memoization Opportunities: If you notice that you can improve a recursive algorithm by memoizing (caching) intermediate results, DP might be a good fit.
- Sequential Dependencies: Problems where the solution depends on the results of previous steps or stages are often candidates for DP. DP is particularly useful when solving problems involving sequences, such as strings, arrays, or graphs.
- Optimization or Counting: DP is often applied to optimization problems (maximizing or minimizing a value) or counting problems (finding the number of possible solutions).
- Recursive Backtracking Inefficiency: If you encounter a recursive backtracking algorithm that is slow due to repeated calculations, this is a clear indication that DP might be a better approach.
- Subproblem Independence: Some problems have subproblems that are entirely independent of each other. In such cases, DP can be applied to solve each subproblem in parallel or any order, making it an efficient choice.
- Limited Set of Choices: Problems where the number of choices at each step is limited and doesn't grow exponentially can often be tackled with DP. DP can explore all possible choices without leading to an impractical number of computations.
Final Thoughts
Dynamic programming is a little like magic: It turns a daunting problem into a series of manageable tasks, making the impossible possible. But unlike a magic trick, the method behind dynamic programming is logical and grounded in sound reasoning.
Sure, getting the hang of it might take some time. You'll need to practice spotting overlapping subproblems and constructing optimal solutions. But once you've mastered these skills, you'll be able to tackle a wide range of problems with newfound efficiency.
Dynamic programming is a useful but advanced skill to learn if one is a programmer or DevOps engineer, particularly if you specialize in Python. It makes complex algorithmic problems easy to digest and its versatility makes it a must-have in the repertoire of every DevOps learning kit. Remember, the journey of a thousand miles begins with a single step – or in our case, a single subproblem.
Cheers and Happy Coding!
FAQs on Dynamic Programming
When should i use dynamic programming.
Use Dynamic Programming when you encounter problems with overlapping subproblems and optimal substructure. Common applications include algorithms for optimization, like finding the shortest path, maximizing profit, or minimizing cost.
Are there different types of Dynamic Programming?
Yes, Dynamic Programming can be categorized into two main types: Memoization (Top-down) and Tabulation (Bottom-up). The choice between them depends on the specific problem and your coding preferences.
Learn more:
The Art of Debugging: Mastering the Bug Hunt, One Error at a Time
Introduction to Object-Oriented Programming
How Software is Developed? A Step-By-Step Guide
Array vs Linked List [When to use What]
7-Step Approach to Solve Any Coding Problem
Our Courses
Practice-Based Learning Tracks, Supercharged By A.I.
Learn C practically and Get Certified .
Popular Tutorials
Popular examples, reference materials, learn c interactively, dsa introduction.
- What is an algorithm?
- Data Structure and Types
- Why learn DSA?
- Asymptotic Notations
Master Theorem
Divide and Conquer Algorithm
Data Structures (I)
- Types of Queue
- Circular Queue
- Priority Queue
Data Structures (II)
- Linked List
- Linked List Operations
- Types of Linked List
- Heap Data Structure
- Fibonacci Heap
- Decrease Key and Delete Node Operations on a Fibonacci Heap
Tree based DSA (I)
- Tree Data Structure
- Tree Traversal
- Binary Tree
- Full Binary Tree
- Perfect Binary Tree
- Complete Binary Tree
- Balanced Binary Tree
- Binary Search Tree
Tree based DSA (II)
- Insertion in a B-tree
- Deletion from a B-tree
- Insertion on a B+ Tree
- Deletion from a B+ Tree
- Red-Black Tree
- Red-Black Tree Insertion
- Red-Black Tree Deletion
Graph based DSA
- Graph Data Structure
- Spanning Tree
- Strongly Connected Components
- Adjacency Matrix
- Adjacency List
- DFS Algorithm
- Breadth-first Search
- Bellman Ford's Algorithm
Sorting and Searching Algorithms
- Bubble Sort
- Selection Sort
- Insertion Sort
- Counting Sort
- Bucket Sort
- Linear Search
- Binary Search
Greedy Algorithms
Greedy Algorithm
- Ford-Fulkerson Algorithm
- Dijkstra's Algorithm
- Kruskal's Algorithm
- Prim's Algorithm
- Huffman Coding
Dynamic Programming
- Floyd-Warshall Algorithm
- Longest Common Sequence
Other Algorithms
Backtracking Algorithm
- Rabin-Karp Algorithm
DSA Tutorials
- What is an Algorithm?
- Longest Common Subsequence
Dynamic Programming is a technique in computer programming that helps to efficiently solve a class of problems that have overlapping subproblems and optimal substructure property.
If any problem can be divided into subproblems, which in turn are divided into smaller subproblems, and if there are overlapping among these subproblems, then the solutions to these subproblems can be saved for future reference. In this way, efficiency of the CPU can be enhanced. This method of solving a solution is referred to as dynamic programming.
Such problems involve repeatedly calculating the value of the same subproblems to find the optimum solution.
- Dynamic Programming Example
Let's find the fibonacci sequence upto 5th term. A fibonacci series is the sequence of numbers in which each number is the sum of the two preceding ones. For example, 0,1,1, 2, 3 . Here, each number is the sum of the two preceding numbers.
We are calculating the fibonacci sequence up to the 5th term.
- The first term is 0.
- The second term is 1.
- The third term is sum of 0 (from step 1) and 1(from step 2), which is 1.
- The fourth term is the sum of the third term (from step 3) and second term (from step 2) i.e. 1 + 1 = 2 .
- The fifth term is the sum of the fourth term (from step 4) and third term (from step 3) i.e. 2 + 1 = 3 .
Hence, we have the sequence 0,1,1, 2, 3 . Here, we have used the results of the previous steps as shown below. This is called a dynamic programming approach .
- How Dynamic Programming Works
Dynamic programming works by storing the result of subproblems so that when their solutions are required, they are at hand and we do not need to recalculate them.
This technique of storing the value of subproblems is called memoization. By saving the values in the array, we save time for computations of sub-problems we have already come across.
Dynamic programming by memoization is a top-down approach to dynamic programming. By reversing the direction in which the algorithm works i.e. by starting from the base case and working towards the solution, we can also implement dynamic programming in a bottom-up manner.
- Recursion vs Dynamic Programming
Dynamic programming is mostly applied to recursive algorithms. This is not a coincidence, most optimization problems require recursion and dynamic programming is used for optimization.
But not all problems that use recursion can use Dynamic Programming. Unless there is a presence of overlapping subproblems like in the fibonacci sequence problem, a recursion can only reach the solution using a divide and conquer approach.
That is the reason why a recursive algorithm like Merge Sort cannot use Dynamic Programming, because the subproblems are not overlapping in any way.
- Greedy Algorithms vs Dynamic Programming
Greedy Algorithms are similar to dynamic programming in the sense that they are both tools for optimization.
However, greedy algorithms look for locally optimum solutions or in other words, a greedy choice, in the hopes of finding a global optimum. Hence greedy algorithms can make a guess that looks optimum at the time but becomes costly down the line and do not guarantee a globally optimum.
Dynamic programming, on the other hand, finds the optimal solution to subproblems and then makes an informed choice to combine the results of those subproblems to find the most optimum solution.
Different Types of Dynamic Programming Algorithms
Table of contents.
- Introduction
- Different Types of Greedy Algorithm
Sorry about that.
Related Tutorials
DS & Algorithms

- Programming
What is Dynamic Programming? Example, Algorithms, Pros & Cons
Home Blog Programming What is Dynamic Programming? Example, Algorithms, Pros & Cons
Embarking on the dynamic programming journey involves breaking down a tough algorithmic problem into smaller pieces, saving their results, and then making them work better to find a complete solution. The main focus is usually on figuring out the biggest and smallest values within the algorithmic query. In this article, I dig into the details of dynamic programming, taking a close look at how it works. Using examples, I'll guide you through the step-by-step process, showing how dynamic programming is a powerful and efficient way to solve problems. By working smartly through smaller problems, this method leads to the best solutions in a systematic way.
Overall, dynamic programming is a strong and effective approach to problem-solving in the world of algorithms, making complex challenges more manageable and solutions more accessible.
.png&w=3840&q=75)
What is Dynamic Programming?
Dynamic programming is a technique of breaking down a problem into smaller problems, solving each sub-problems once, storing the solutions of these sub-problems, and eventually finding a solution to the original problem.
We break down a big problem into smaller problems. Typically, the smaller problems are similar to the parent problem only difference being the scale. Thus, these sub-problems can also be divided further smaller sub-problems until we achieve problems that cannot be further divided. You can imagine we have a tree of a problem and their sub-problems. We start with solving the “leaf” level problems and then move on to their “parent” problems and so on. We save the results as we solve sub-problems for future reference. Thereby avoiding working on the same sub-problem if encountered again.
This approach is like the divide and conquers algorithm where a problem is divided into sub-problems and recursively solving sub-problems and combining their solution to find the solution to the real problem.
Dynamic Programming Characteristics
It is important to know when to use dynamic programming algorithms. There are two major characteristics to identify whether dynamic programming is the right fit.
1. Optimal Substructure
The problem should have optimal substructure properties. It means that the optimal solution can be evaluated from the optimal solutions of its sub-problems. This will also help you define the base case of the recursive algorithm.
Consider an example of the Fibonacci series. We define the n th number as the sum of the previous 2 numbers.
2. Fib(n) = Fib(n-1) + Fib(n-2)
We can see that a problem of size “ n ” can be broken down into sub-problems of size “ n-1 ” and “ n-2 ”. We also know solutions of base cases, i.e., f(0) as 0 and f(1) 1. as 1.
3. Overlapping subproblems
The other necessary property is overlapping sub-problems. A problem is said to have overlapping sub-problem properties if the sub-problems can be seen recursively visiting the same sub-problems. In such cases, we can improve the performance of an algorithm by storing the results of each sub-problem once it is calculated.

As seen above, in the case of Fibonacci dynamic programming numbers tree representation, several sub-problems like fib(4), fib(3), fib(2), and so on can be seen occurring multiple times.
Note that both optimal substructure and overlapping sub-problems dynamic programming patterns are required for a problem to be a dynamic programming problem.
Example of Dynamic Programming
One can easily find a lot of dynamic programming examples on the internet. We will discuss one of the popular examples here.
Consider a rod of length n inches and an array of prices that includes prices of all pieces of size smaller than n . We need to determine the maximum sum of money we can make by cutting up the rod and selling the pieces.
length | 1 2 3
--------------------
price | 1 5 8
With the above set of prices, if the length of the rod is 4, we can get a maximum value of 10 by cutting the rod into two pieces of length 2.
The image below shows that the problem can be broken down into smaller sub-problems, which can further be broken down into smaller sub-problems. We also know the solution of the base case, i.e., the price of length 0 is 0. This depicts the property of optimal substructure.
We can also see that the same sub-problems (highlighted in color) are being repeated. This confirms that the problem has an overlapping sub-problem characteristic.
To solve this problem, we divide the rod of length n into two parts: i and n-i. We repeat this process for the second part and divide n-i further in the same fashion. We store the maximum profit for each length i of the rod. In the end, the maximum of all values will be the expected value.
Here is a code snippet in java. This gives you an idea about the implementation of dynamic programming in java.
Dynamic Programming Techniques GeeksforGeeks
There are two dynamic programming methods of implementation.
1. Top-Down Approach
This approach solves the bigger problem by recursively solving smaller sub-problems. As we solve the sub-problems, we store the result for later use. This way, we don’t need to solve the same sub-problem more than once. This method of saving the intermediate results is called Memoization (not memorization).
2. Bottom-Up Approach
The bottom-up method is an iterative version of the top-down approach. This approach starts with the smallest and works upwards to the largest sub-problems. Thus when solving a particular sub-problem, we already have results of smaller dependent sub-problems. The results are stored in an n -dimensional ( n=>0 ) table. Thus, you can imagine when we arrive at the original problem, we have solved all its sub-problems. Now we just use the result set to find the best solution. This method is called Tabulation.
Which one is better?
- The top-down approach is typically recursive. It has the overhead of recursive calls and therefore is slower than the bottom-up approach.
- One might find the top-down approach easier to implement because we use an array of some sort of lookup table to store results during recursion. While for the bottom-up approach we need to define the order of iteration and define an n -dimensional table for storing results.
- The top-down approach might also run into stack overflow conditions in the case of a very deep recursion tree.
Dynamic Programming Algorithms
1. greedy algorithms.
Greedy algorithms are problem-solving strategies that make locally optimal choices at each step with the hope of finding a global optimum. In a greedy algorithm, decisions are made based on the current best option without revisiting or reconsidering previous choices. While this approach doesn't guarantee the absolute best solution, it often produces acceptable results and is commonly used for optimization problems like minimum spanning trees, coin change, and scheduling.
2. Floyd-Warshall Algorithm
The Floyd-Warshall algorithm is a dynamic programming technique used for finding the shortest paths between all pairs of vertices in a weighted graph. It considers all possible paths and systematically updates the shortest path distances between every pair of vertices until the optimal solution is reached. This algorithm is particularly useful for scenarios where the graph may contain negative weight edges.
3. Bellman Ford Algorithm
The Bellman-Ford algorithm is employed for finding the shortest path from a source vertex to all other vertices in a weighted graph, even in the presence of edges with negative weights. This algorithm iteratively relaxes edges, adjusting distance estimates until the optimal solution is achieved, or a negative weight cycle is detected. The Bellman-Ford algorithm is valuable for scenarios where graphs may contain negative weight edges, which can pose challenges for other algorithms like Dijkstra's.
How to Solve Dynamic Programming Problems? [In 4 Steps]
We will understand the steps with a popular example: The coin change problem with dynamic programming.
You are given coins of varying denominations and asked to pay a certain amount with the fewest coins possible. How do you write a program for this?
Step 1: Identify the sub-problem and write it down in words
Start by defining the problem statement in programmable constructs.
There is an array of coins with varying denominations and an integer sum representing the total amount of money. We need to return the fewest coins (values from the array) required to make up that sum. If that sum cannot be accumulated with given denominations, return -1. We will assume that infinite coins are available for the given denominations.
Now we break down the problem into smaller variations. Start with assuming real values for which you know the solution. For example, if the sum is 40 and the denominations are {1, 5, 10, 25}. If you work it out on paper, you can see that you need three coins: 25, 10, and 5. There are other possibilities, but incorrect, solutions like {5, 5, 5, 5, 5, 5, 5, 5}, {10, 10, 10, 5, 5} and so on.
To find the sub-problem, we can see that the sum of two numbers can express any amount. These numbers can be further expressed as the sum of two numbers.
The smallest number, 1, is present in the denomination. So any number n can be expressed as 1 + ( n – 1).
Step 2: Sub-problem expressed as Mathematical recurrence
In the above case, the sub-problem can be expressed as. case, sub-problem can be expressed as.
min_coins ( 40 ) = min_coins ( 40 — c) + 1
Where c is the number of the allowed denomination.
This equation can be made generic by replacing 40 with n .
min_coins (n) = min_coins (n — c) + 1
Step 3: Define memoization array strategy to fill it
We know that the problem has characteristics of overlapping sub-problems. We can use the memoization technique to cache the results of sub-problems for later use.
In this case, we can simply use an array of lengths as the given amount. We will store the minimum coins required for a particular sub-amount, an index of the same value. This makes it easier to fetch the result when required.
Step 4: Coding the solution
While coding the algorithm, one can start with the initialization of the array (or cache) if required. Next, one should set the base case. Each problem can be solved in multiple ways using the dynamic programming approach. You need to think about which one suits you.
Below is the dynamic programming python implementation of the above-discussed problem. However, dynamic programming algorithms can be implemented in any language. If you want to use python, Python Programming certification is a great starting point.
For coin-in coins:
Else :
else:
Advantages of Dynamic Programming
- Dynamic programming can be used to obtain local as well as the total optimal solution.
- Dynamic programming algorithms are generally compact code pieces as they are based on recursive functions.
- The linear and non-linear problem, both kind of problems can be solved using dynamic programming.
- Dynamic programming algorithms are easy to debug.
Disadvantages of Dynamic Programming
- Dynamic programming uses recursion, which requires more memory in the call stack, and leads to a stack overflow condition in the runtime.
- It takes memory to store the solutions of each sub-problem. There is no guarantee that the stored value will be used later in execution.
- High memory usage might lead to degraded performance. It depends on the dynamic programming algorithm and the programming language. For java, you can do Java certification to be able to use java efficiently.
In summary, my journey through the Dynamic Programming Algorithm has been marked by enlightening discoveries and practical applications. By integrating real-life case studies and examples, I aim to underscore the substantial impact of DP on effective problem-solving. Reflecting on my roles as an enthusiast, expert, and practitioner, I am assured that Dynamic Programming will persist as a cornerstone in algorithmic optimization.
It provides a resilient framework for addressing intricate challenges, offering both a strategic approach and tangible solutions. As the significance of DP continues to unfold, it stands poised to remain an essential tool, shaping the landscape of efficient problem-solving in the evolving realms of algorithms and optimization..
Frequently Asked Questions (FAQs)
There are numerous applications of dynamic programming in real life. Finding the shortest path between the source and multiple destinations. Git merge uses DP coding to find the longest common subsequence. There are other applications like image processing, optimal inventory management, production optimization, genetic algorithms, and matrix multiplication dynamic programming; the list is endless.
Recursion is calling a function within itself. Sub-problems might have to be solved multiple times when a problem is solved using recursion. At the same time, Dynamic programming is a technique where you store the result of the previous calculation to avoid calculating the same once again.
Algorithms that are aimed at solving optimization problems use a dynamic programming approach. Examples of dynamic programming algorithms are string algorithms like the longest common subsequence, longest increasing subsequence, and the longest palindromic substring. Optimizing the order for chain matrix multiplication. The Bellman-Ford algorithm for finding the shortest distance in a graph.

Paresh Patil
Paresh is a Software developer by profession with a major experience in big data and backend development. Along with writing quality code and implementing robust system design, he takes a keen interest in generating maximum value for end-user. He loves "chai" and trekking.
Avail your free 1:1 mentorship session.
Something went wrong
Upcoming Programming Batches & Dates
| Name | Date | Fee | Know more |
|---|
LTCWM > Blog > Resources > Technical guides > How to Solve Any Dynamic Programming Problem

How to Solve Any Dynamic Programming Problem
Updated on April 12th, 2020 | Sign up for learn to code tips
If you’re aiming for a top-tier tech job, you have to face the coding interview —and come out on top. And one sure-fire way to impress is to have dynamic programming down pat.
In today’s special guest post, Sam Gavis-Hughson guides us through his formula for solving any dynamic programming problem.
Take it away, Sam!
Disclosure: I’m an affiliate for Sam's courses. While the resources mentioned in this post are free, I may get a small commission if you click the links below and later buy one of his products. Thanks!
When it comes to coding interviews , not all topics are created equal.
Some are relatively easy. For example, even the hardest linked list problems don’t tend to be that difficult because the concept is on the simpler side.
But then there are some topics where even the easiest variations strike fear into the hearts of interviewees everywhere.
One such topic is dynamic programming —an optimization technique programmers can use to speed up our code when we are repeatedly solving the same problem.

Dynamic programming has truly become the defacto hard topic that your interviewer can ask you. If they want to really put you through your paces, that’s what they’ll ask about.
This means that if you’re interviewing for any top tech company , dynamic programming should be at the top of your list of topics to prepare.
What is Dynamic Programming?
Essentially, dynamic programming is a way of making a recursive algorithm more efficient by making sure it doesn’t have to solve the same subproblem twice.
When you use dynamic programming, it stores the results of subproblems so you don’t have to re-compute those results next time they’re needed. It’s an alternative to plain recursion, which requires repeating the solution process every time the subproblem is encountered.
This Stack Overflow answer words it well: “Dynamic programming is when you use past knowledge to make solving a future problem easier.”
Some benefits of dynamic programming are that it saves you coding time, reduces lines of code, and speeds up an algorithm’s processing time.
Now, here’s the crazy thing…
Dynamic Programming Doesn’t Have to Be Hard
The real challenge with dynamic programming is that it is counterintuitive. When you’re trying to solve dynamic programming problems, all the obvious steps that you would normally take actually pull you further away from the correct solution:
- Want to find the optimal solution? You actually need to start with the brute force approach.
- Want to find an iterative solution? You have to start with recursion.
- Want to solve the problem as quickly as possible? You need to slow it down and go step by step.
Click To Tweet
So if dynamic programming is so counterintuitive, how are we ever supposed to solve these problems effectively?
To start, let’s look at how most people prepare for their coding interviews:
They focus on memorizing solutions.
Rather than being strategic and understanding the underlying techniques, most people focus on simply memorizing as many solutions as they can.
Memorizing gives you a quick and easy win. But the problem is that it ultimately handicaps you.
When you focus on memorizing, your interview prep strategy becomes very simple: just go through as many problems as you can. When you go into an interview, you hope that you see a problem that you’ve studied before.
But this approach quickly leads to diminishing returns. There’s only so much that you can actually memorize, and the number of problems that you could be asked is very large.
Not to mention that this approach prevents you from actually being able to connect the dots.
Imagine learning a new language (let’s say French). You decide that you are going to create a massive deck of flashcards and simply memorize individual words. This is your plan to get to fluency.

So you start memorizing. Here’s one sample set of words:
“suis”, “es”, “est”, “sommes”, “êtez”, “sont”
What is the connection between these words (if you already know French, pretend you don’t for a sec)?
On the surface, it’s not obvious. So if you were just memorizing, you would be memorizing 6 discrete words.
However, there actually is a very close connection between these words: They’re all different conjugations of the verb “to be.”
If we look at the translations, we see:
- “Je suis” – “I am”
- “Tu es” – “You are”
- “Elle est” – “She is”
- “Nous sommes” – “We are”
- “Vous êtez” – “You all are”
- “Ils sont” – “They are”
Notice how much easier this is now that we’ve connected them all in some way that is meaningful to us? Yes we still need to memorize the specifics, but now we can see what connects them.
So what if we could do the same thing with dynamic programming?
Well, it’s never going to happen if we just try to memorize solutions to different problems. The issue is that the similarity between these different problems ISN’T in the solution itself.
The similarity between all dynamic programming problems is in the process.

For the rest of this post, I’m going to show you the exact strategy that you can use to solve any dynamic programming problem, even if you’ve never seen the problem before.
The remainder of this post is excerpted from my free ebook, Dynamic Programming for Interviews, which you can download here .
How to Solve Dynamic Programming Problems Using the Fast Method
What is the most important characteristic of any successful interviewee?
They have a repeatable strategy.
That’s exactly what the FAST Method is. It’s a repeatable strategy for solving any dynamic programming problem, whether you’ve seen the problem before or not.
The FAST Method is an acronym for the 4 steps you need to solve any dynamic programming problem:
- F ind the First Solution
- A nalyze the First Solution
- Identify the S ubproblems
- T urn around the solution
By following these 4 steps, you’ll be able to find the optimal dynamic programming solution for any problem.
Start coding now
Stop waiting and start learning! Get my 10 tips on teaching yourself how to code.
Success! Now check your email to confirm your subscription.
There was an error submitting your subscription. Please try again.
1. Find the First Solution
The first step for any dynamic programming problem (and the step that most people skip) is to find an initial brute-force solution to the problem.
The goal here is to just get something down on paper without any concern for efficiency. To be honest, this should be the first step for any problem you might solve, but it is particularly important for dynamic programming.

There are several keys to think about while doing this step that you’ll want to keep in mind:
- The solution should be recursive. If not, the problem probably isn’t a good candidate for dynamic programming. For a lot more info on effectively coming up with a recursive solution, look here .
- Each recursive call must be self-contained. This means that you cannot store your results to a global variable or pass a results variable into your function. I often refer to the required approach as “building up as you return” and you can learn more about that here .
- It is important that we minimize the number of variables that we are passing into our recursive function. Dynamic programming solutions rely on there being multiple recursive calls with the same input, and the more variables there are, the less the inputs will overlap.
With these basic rules in mind, you will have no trouble using this brute force solution in the FAST Method.
Check out Dynamic Programming for Interviews for detailed walkthroughs of 5 of the most popular dynamic programming problems.
2. Analyze the First Solution
This is the step where we decide whether we can actually use dynamic programming to solve a problem. To do this, we’re going to look at a couple of specific things.
First off, we should be sure to determine what the actual time complexity of our code is currently. One mistake that I see fairly often is attempting to optimize something that doesn’t need to be optimized. If our solution is already efficient, spending a lot of time optimizing is a real waste of time.
With most of our recursive functions, we can use a pretty simple heuristic to compute the runtime. We simply look at the branching factor of our recursive function raised to the depth.
For example, if we were finding all combinations of an input, that would give us a time complexity of `O(2n)`. You can read a lot more about this here .

Next up, if our solution is in fact inefficient (we’re most likely looking for something that is exponential time or worse as being inefficient), we want to see if we can optimize it using dynamic programming.
Dynamic programming actually requires us to meet 2 specific criteria. If we don’t, then it is not possible for us to optimize our problem using dynamic programming. However, if we do, we will likely see a major improvement.
These are the criteria that we need to look for:
Optimal Substructure
The first criterion is that our problem must have optimal substructure. Technically speaking, this means that we must be able to find an optimal solution to a problem by solving for its subproblems. An easier way to think about this is simply that we must be able to solve the problem recursively. If we already found a recursive problem in the previous step, then we can safely assume we have optimal substructure.
Overlapping Subproblems
This is where the actual optimization comes in. If our problem has overlapping subproblems, that means that we are calling the same function with the exact same inputs multiple times. So we’re doing repetitive work for no reason. If we were to cache (or “memoize”) the results, we would be able to save a lot of time.
If we meet these two criteria, then we know that we can optimize our solution using dynamic programming.
3. Identify the Subproblems
If we find that we are able to use dynamic programming, the next step is to clearly identify the subproblems. Defining the subproblem in plain English is going to make it much easier for us to understand everything that is going on.

To approach this step, we are going to specifically look at our recursive code and see what recursive calls are being made. We then want to define in plain English what the actual meaning of that recursive call is.
For example, if we are computing the nth Fibonacci number, we have 2 recursive calls, fib(n-1) and fib(n-2). To define these in plain English, the function simply returns the nth Fibonacci number. Pretty simple.
Once we’ve identified what the subproblems are, we can also memoize our recursive solution to make it more efficient. All this means is that we are going to add an array or HashMap that stores all of the values that we’ve previously computed.
Each time we make a function call, we will look in our array to see if a result has already been computed for the current inputs. If so, then we can return it without actually computing anything. If not, we compute it and then save it into our array.
For full code and example problems, download Dynamic Programming for Interviews .

4. Turn Around the Solution
If you’ve ever spent any serious time studying dynamic programming solutions in the past, you may have noticed that the vast majority of them are iterative, not recursive. And yet up to this point in the FAST Method, we have only generated recursive solutions.
In this optional final step of the process, we will take our recursive solution and make it into an iterative solution.
When doing dynamic programming, we really have two different options:
- A top-down (memoized) solution
- A bottom-up (tabular) solution
A top-down solution is the recursive solution that we found in the previous step. We call this top-down because we are starting with the goal result that we’re trying to get (ie. fib(5)) and then repeatedly split it into smaller subproblems until we reach our base case.
Bottom-up is simply the opposite of that. Rather than starting with our target input, we start with the base cases. We iteratively compute larger and larger subproblems until we reach our target result.
Both of these approaches will give us the same worst case complexity. However, many people prefer the bottom-up approach because recursive code tends to execute slower than iterative code that does the same work, given that it requires additional overhead.

The key to turning around the solution and finding a bottom-up solution is to look at what the smallest subproblems are. This is why we needed to carefully identify and define the subproblems in the previous step.
We can start with computing our base case. Then we need to determine how to compute a given subproblem, assuming all the smaller subproblems have already been computed. We’ll save all of these subproblem solutions into an array so that we can easily look them up.
See examples of exactly how to do this in my free ebook, Dynamic Programming for Interviews .
At the end of the day, dynamic programming is a challenging topic. It’s not something that you can magically become a master at overnight.
However, it also isn’t something you have to be afraid of. If you nail down your recursion skills and understand the FAST Method, even the most challenging dynamic programming problems can be easily solved during your interview.
Next Steps : Where to Learn More About Dynamic Programming
Want to learn more about dynamic programming? Check out these online courses:
- Intro To Dynamic Programming – Coding Interview Preparation (Udemy): Specifically designed to help you gain foundational knowledge for your software engineering coding interview
- Dynamic Programming – I (Udemy): Also intro-level and geared toward coding interview basics
- Master the Art of Dynamic Programming (Udemy): In-depth theory and practice of dynamic programming
- Learn Dynamic Programming Using Python (Udemy): Hones in specifically on dynamic programming in the Python programming language
- Greedy Algorithms, Minimum Spanning Trees, and Dynamic Programming (Coursera): A course offered by Stanford about dynamic programming and other algorithm-related topics
- Dynamic Programming: Applications in Machine Learning and Genomics (edX): Learn about two interesting applications of dynamic programming that meld science and technology, from UC San Diego
About the Author

Sam Gavis-Hughson, founder of Byte by Byte, helps software engineers successfully interview for jobs at top tech companies. He is the author of Dynamic Programming for Interviews , the ebook that shows anyone how to succeed at dynamic programming interviews.
What is Dynamic Programming? Solve Complex Problems with Ease self.__wrap_b=(t,n,e)=>{e=e||document.querySelector(`[data-br="${t}"]`);let a=e.parentElement,r=R=>e.style.maxWidth=R+"px";e.style.maxWidth="";let o=a.clientWidth,c=a.clientHeight,i=o/2-.25,l=o+.5,u;if(o){for(;i+1 {self.__wrap_b(0,+e.dataset.brr,e)})).observe(a):process.env.NODE_ENV==="development"&&console.warn("The browser you are using does not support the ResizeObserver API. Please consider add polyfill for this API to avoid potential layout shifts or upgrade your browser. Read more: https://github.com/shuding/react-wrap-balancer#browser-support-information"))};self.__wrap_b(":Rid9j6:",1)
What is Dynamic Programming?
Principles of dynamic programming, when to use dynamic programming, example: fibonacci numbers.
Dynamic programming is a powerful technique used in computer science, mathematics, and operations research to solve complex problems by breaking them down into simpler, overlapping subproblems. It is particularly useful for optimization problems, where the objective is to find the best solution among a set of possible solutions. Dynamic programming can be applied to a wide range of problems, including sequence alignment, shortest path routing, and resource allocation. In this blog post, we will delve into the concept of dynamic programming, explore its principles, and learn how to implement it in code. By the end of this post, you should have a solid understanding of dynamic programming and how it can help you solve complex problems with ease.
Dynamic programming is a technique used to solve problems by dividing them into simpler, overlapping subproblems and combining their solutions to construct the optimal solution. It is based on the idea of recursion, where a problem is solved by breaking it down into smaller instances of the same problem. Unlike naive recursion, however, dynamic programming stores the results of each subproblem in a data structure called a "memoization table," allowing us to avoid redundant computations.
The two main approaches to dynamic programming are top-down and bottom-up:
- Top-down (Memoization): In this approach, we start by solving the original problem and recursively break it down into smaller subproblems. Whenever we encounter a subproblem that has already been solved, we simply look up its solution in the memoization table, thus reducing the overall time complexity. This approach is also called "memoization."
- Bottom-up (Tabulation): In this approach, we iteratively build up solutions to the problem, starting from the simplest subproblems and gradually working our way up to the original problem. This method fills in the memoization table iteratively, ensuring that all required subproblem solutions are available before solving the main problem. This approach is also called "tabulation."
There are two key principles underlying dynamic programming:
- Optimal Substructure: This principle states that the optimal solution to a problem can be constructed from optimal solutions to its subproblems. This means that if we can find the best solution for each subproblem, we can use these solutions to create the optimal solution for the main problem.
- Overlapping Subproblems: This principle states that a problem can be broken down into smaller subproblems that are solved independently, and their solutions are reused multiple times. This allows us to use memoization or tabulation techniques to store the results of subproblems and avoid redundant computations, thus improving the efficiency of the algorithm.
Dynamic programming can be applied to problems that exhibit the following characteristics:
- Optimal substructure: The problem can be broken down into smaller, overlapping subproblems, and the optimal solution to the main problem can be constructed from the optimal solutions of these subproblems.
- Overlapping subproblems: The problem can be solved by solving smaller instances of the same problem, and these smaller instances are solved multiple times during the course of solving the main problem.
To illustrate the concept of dynamic programming, let's consider the classic problem of computing the Fibonacci numbers. The Fibonacci sequence is defined as follows:
- F(n) = F(n-1) + F(n-2) for n > 1
Naive Recursion
A naive recursive solution to compute the nth Fibonacci number can be implemented as follows:
In this implementation, we store the computed Fibonacci numbers in a dictionary called memo . This way, we avoid recomputing overlapping subproblems and reduce the time complexity to O(n).
Dynamic Programming: Bottom-Up Approach (Tabulation)
Now, let's implement the bottom-up approach using tabulation:
In this implementation, we iteratively fill in the table array with the Fibonacci numbers, starting with the simplest cases (F(0) and F(1)) and working our way up to F(n). This approach has a time complexity of O(n) and does not require recursion.
Q: What are the main differences between memoization and tabulation?
A: Memoization is a top-down approach that utilizes a memoization table to store the results of subproblems. It relies on recursion to break down the main problem into smaller subproblems. Tabulation, on the other hand, is a bottom-up approach that iteratively builds up solutions, starting from the simplest subproblems and working its way up to the main problem. Both methods use memoization tables to store intermediate results, but they differ in their strategies for filling in these tables.
Q: When should I use dynamic programming?
A: You should consider using dynamic programming when the problem exhibits optimal substructure and overlapping subproblems. This means that the problem can be broken down into smaller, simpler subproblems, and their solutions can be combined to construct the optimal solution to the main problem. Additionally, these subproblems should be solved multiple times during the course of solving the main problem, allowing you to benefit from memoization or tabulation techniques.
Q: Can dynamic programming be used for problems other than optimization?
A: Yes, dynamic programming can be applied to various types of problems, including counting problems, combinatorial problems, and decision-making problems. As long as a problem exhibits optimal substructure and overlapping subproblems, dynamic programming can be a useful technique for solving it efficiently.
Q: How do I choose between the top-down and bottom-up approaches?
A: The choice between top-down and bottom-up approaches depends on the problem at hand and your specific requirements. The top-down approach (memoization) is usually easier to implement, as it closely follows the problem's natural recursive structure. However, it can lead to higher memory usage due to recursion. The bottom-up approach (tabulation) may require more careful planning to build up the solutions iteratively, but it can often lead to lower memory usage and better cache performance. Consider your specific problem and constraints todetermine the most appropriate approach.
Q: Are there any limitations to dynamic programming?
A: Dynamic programming has some limitations. First, it may not be applicable to problems that do not exhibit optimal substructure and overlapping subproblems. Second, the time complexity of dynamic programming algorithms can still be quite high for some problems, especially those with large input sizes or complex memoization tables. Lastly, dynamic programming may lead to increased memory usage due to the need to store intermediate results in memoization tables.
Dynamic programming is a powerful technique that can help you solve complex problems with ease by breaking them down into simpler, overlapping subproblems. By using memoization or tabulation, dynamic programming can significantly reduce the time complexity of algorithms and improve their efficiency. Understanding the principles of dynamic programming and learning how to implement it in code can greatly enhance your problem-solving skills and expand your toolbox as a programmer or computer scientist.
We hope this blog post has provided you with a clear understanding of dynamic programming and its applications. With this knowledge, you are now better equipped to tackle a wide range of challenging problems that may have seemed daunting before.
Sharing is caring
Did you like what Mehul Mohan wrote? Thank them for their work by sharing it on social media.
No comment s so far
Curious about this topic? Continue your journey with these coding courses:
3.34k students learning
Piyush Garg
Mastering Algorithms
Dynamic Programming for Beginners – How to Solve Coding Challenges with Memoization and Tabulation
Dynamic Programming is style of coding where you store the results of your algorithm in a data structure while it runs.
Understanding Dynamic Programming can help you solve complex programming problems faster.
These methods can help you ace programming interview questions about data structures and algorithms. And they can improve your day-to-day coding as well.
We released a 5-hour course on Dynamic Programming on the freeCodeCamp.org YouTube channel.
Alvin Zablan developed this course. Alvin is an experienced programming instructor at Coderbyte, a popular website for technical interview prep and coding challenges.
In this course you will learn to use Dynamic Programming strategies to solve programming challenges such as:
- Calculating the 40th number of the Fibonacci sequence.
- Counting the number of different ways to move through a 6x9 grid.
- Given a set of coins, how can you make 27 cents in the least number of coins.
This course uses images and animations to help you visualize problems and important concepts. After understanding problems conceptually, you will learn how to solve them in JavaScript using Dynamic Programming.
Even though this course uses JavaScript, you will learn concepts and knowledge that you can apply to other programming languages, including Python.

Dynamic Programming Methods This Course Covers
Part one of this course focuses on Memoization methods. This is where you use recursion and store the intermediate results of your algorithm. You can then access those results on later trips through your your loops.
Here are the Memoization strategies this course covers:
- fib memoization
- gridTraveler memoization
- memoization recipe
- canSum memoization
- howSum memoization
- bestSum memoization
- canConstruct memoization
- countConstruct memoization
- allConstruct memoization
And part two focuses on Tabulation strategies. These involve building up a table of data iteratively.
Here are the Tabulation strategies this course covers:
- fib tabulation
- gridTraveler tabulation
- tabulation recipe
- canSum tabulation
- howSum tabulation
- bestSum tabulation
- canConstruct tabulation
- countConstruct tabulation
- allConstruct tabulation
You can watch the full course on the freeCodeCamp.org YouTube channel (5-hour watch).
I'm a teacher and developer with freeCodeCamp.org. I run the freeCodeCamp.org YouTube channel.
If you read this far, thank the author to show them you care. Say Thanks
Learn to code for free. freeCodeCamp's open source curriculum has helped more than 40,000 people get jobs as developers. Get started
Code With C
The Way to Programming
- C Tutorials
- Java Tutorials
- Python Tutorials
- PHP Tutorials
- Java Projects
Dynamic Programming: Strategies for Solving Complex Problems Efficiently
Dynamic Programming Demystified 🚀
Hey there, fellow tech enthusiasts! 🤖 Today, let’s delve into the fascinating world of Dynamic Programming 🌟. Don’t be scared off by the jargon; I’m here to break it down with a sprinkle of humor and a dollop of enthusiasm! So, grab your virtual seat and let’s dive right in! 💻
Understanding Dynamic Programming
So, what in the world is Dynamic Programming ? 🤔 Imagine you have this colossal problem to solve, and it’s so complex that you feel like pulling your hair out! Dynamic Programming swoops in like a superhero, offering you a strategy to break down this mammoth task into bite-sized, manageable chunks. Voila! Problem solved! 💪
Definition of Dynamic Programming
Dynamic Programming is like the master chef in the kitchen of algorithms . It’s a methodical way of solving complex problems by breaking them down into simpler subproblems. 🍳 Each subproblem’s solution is stored to avoid redundant calculations, making the overall process more efficient. Efficiency for the win! 🎉
Importance of Dynamic Programming
Picture this: You’re at a buffet, and you want to sample every dish. Dynamic Programming allows you to do just that in the realm of algorithms – optimize your solutions and tackle even the most intricate problems with finesse. It’s like having a secret recipe book for cracking challenging puzzles in record time! 🍽️
Basic Principles of Dynamic Programming
Let’s talk about the fundamental rules that make Dynamic Programming the rockstar of problem-solving techniques! 🌟
- Overlapping Subproblems : It’s like finding money in the pockets of your old jeans. Dynamic Programming identifies these recurring subproblems and saves their solutions for later use, eliminating unnecessary work. It’s all about efficiency, baby! 💸
- Optimal Substructure : This principle is like building a sturdy LEGO tower. Each piece (subproblem) fits perfectly to create the optimal solution . Dynamic Programming ensures that each subproblem’s solution contributes to the overall best answer. It’s all about that solid foundation! 🏗️
Strategies for Applying Dynamic Programming
Now that we’ve got the basics under our belt, let’s explore the two dynamic strategies that make the magic happen! 🎩✨
- Top-down Approach : Imagine you’re skydiving from the top. This approach starts with the main problem and recursively breaks it down into subproblems. It’s adventurous, exhilarating, and definitely keeps you on your toes! 🪂
- Bottom-up Approach : Ever built a tower from the ground up? That’s the bottom-up approach. You start with the smallest subproblems, gradually solving larger ones until you conquer the main problem like a champ. It’s a steady climb to success! 🗼
Applications of Dynamic Programming
Dynamic Programming isn’t just a fancy term; it’s the powerhouse behind some incredible real-world applications! 🌐 Let’s take a peek at a couple of them:
- Fibonacci Sequence : Ah, the Fibonacci sequence, nature’s favorite mathematical marvel ! Dynamic Programming nimbly calculates Fibonacci numbers faster than you can say “Golden Ratio.” It’s all about those efficient number-crunching skills! 🔢
- Shortest Path Algorithms : Navigating through a maze? Dynamic Programming has your back! It’s the GPS guiding you through the shortest route with speed and precision. Say goodbye to taking the long, scenic route! 🗺️
Challenges and Tips for Mastering Dynamic Programming
Ah, every hero has their kryptonite, right? Let’s uncover some challenges in mastering Dynamic Programming and how to conquer them like a pro! 🦸♂️
- Identifying Optimal Substructure : Sometimes the forest (complex problem) is so dense that you can’t see the trees (optimal substructure). Mastering Dynamic Programming involves honing your detective skills to spot these crucial patterns. Sherlock, who? 🕵️
- Handling State Transitions efficiently : It’s like switching gears in a Formula 1 race. Efficiently transitioning between states is key to zipping through problems with ease. Rev up those mental engines and zoom past any hurdles! 🏎️
Overall, Mastering Dynamic Programming Like a Pro! 🚀
So, there you have it, folks! Dynamic Programming, the unsung hero of problem-solving, ready to tackle any challenge with finesse. Remember, practice makes perfect, and with a dash of determination and a sprinkle of creativity, you’ll be mastering Dynamic Programming like a seasoned pro in no time! 💪
Thanks for tuning in, and remember: Keep coding, keep smiling, and embrace the dynamic journey ahead! 🌟
Stay Dynamically Awesome, Techies! 🚀👩💻
In closing, thanks a ton for joining me on this Dynamic Programming rollercoaster! 🎢 Keep shining bright and solving those tech puzzles like a boss! See you in the next coding adventure! ✨
Program Code – Dynamic Programming: Strategies for Solving Complex Problems Efficiently
Code Output: The 10th Fibonacci number is: 55
Code Explanation:
In the given dynamic programming example , we solve for the nth Fibonacci number, a popular problem showcasing the elegance and efficiency of the dynamic programming approach. The recursive nature of the Fibonacci sequence, where each number is the sum of the two preceding ones (excluding the first two numbers which are both considered as 1), makes it an ideal candidate for dynamic programming, particularly memoization.
The code defines a fibonacci function that takes two arguments: n , the position in the Fibonacci sequence whose value we want to find, and memo , a dictionary used as a cache to store the results of the Fibonacci numbers we’ve already computed.
At the function’s core, we employ a base case for when n is less than or equal to 2. For these cases, we simply return 1, as the first two Fibonacci numbers by definition are 1.
The true power and efficiency lie in the subsequent lines. Before plunging headlong into a recursive frenzy, we first check if our current n is in the memo . If it’s not, this means we haven’t computed it yet, and then we proceed to perform the recursive operations to calculate fibonacci(n-1) and fibonacci(n-2) . Crucially, we then store this computed value in memo[n] . This storage step is what saves us from the redundant work if we encounter the same n value again in our computations.
In essence, any subsequent calls for the same Fibonacci number won’t have to go through the recursion again; instead, they’ll directly fetch the result from our memo , dramatically reducing the time complexity from what would have been exponential in a naive recursive approach (O(2^n)) to O(n) in our dynamic programming approach.
Let’s not forget—the function concludes by returning the memoized or newly computed value of the nth Fibonacci number, giving us our desired result efficiently and elegantly. Dynamic programming, with its memoization strategy, thus transforms an otherwise computationally intensive problem into a tractable one, showcasing its power in optimizing the performance of algorithms dealing with overlapping subproblems.
Frequently Asked Questions (F&Q) on Dynamic Programming
What is dynamic programming and how does it work.
Dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It involves solving each subproblem only once and storing the solution to avoid redundant calculations. This approach can significantly improve the efficiency of solving problems with overlapping subproblems.
When should I use dynamic programming to solve a problem?
Dynamic programming is most useful when a problem can be broken down into overlapping subproblems, and the optimal solution to the problem can be constructed from optimal solutions to its subproblems. It is commonly used in optimization problems, such as finding the shortest path or maximizing profit.
What are the key characteristics of problems that are suitable for dynamic programming?
Problems suitable for dynamic programming usually exhibit two key characteristics: optimal substructure and overlapping subproblems. Optimal substructure means that the optimal solution to the problem can be constructed from the optimal solutions to its subproblems. Overlapping subproblems refer to the fact that the same subproblems are solved multiple times in a recursive algorithm .
Can you provide an example of a problem that can be solved using dynamic programming?
One classic example of a problem solved using dynamic programming is the Fibonacci sequence. By storing the results of subproblems (calculating Fibonacci numbers for smaller indices), we can avoid redundant calculations and compute the nth Fibonacci number efficiently.
Are there different strategies or approaches to dynamic programming?
Yes, there are several strategies for approaching dynamic programming problems, such as top-down with memoization and bottom-up with tabulation. Top-down with memoization involves solving the problem recursively while storing the results of subproblems to avoid redundant calculations. Bottom-up with tabulation involves solving the problem iteratively, starting from the smallest subproblems and building up to the desired solution.
What are some common pitfalls to avoid when using dynamic programming?
One common pitfall when using dynamic programming is not recognizing the overlapping subproblems and failing to store and reuse intermediate results. It is essential to identify the repeating subproblems to benefit from the efficiency of dynamic programming . Additionally, starting with a brute-force approach before optimizing with dynamic programming can help in understanding the problem better.
How can I improve my skills in dynamic programming?
To improve your skills in dynamic programming, practice solving a variety of problems that can be optimized using dynamic programming techniques . Online coding platforms, coding contests, and algorithmic problem-solving websites offer a wide range of problems to help you sharpen your skills. Additionally, studying different dynamic programming patterns and approaches can enhance your problem-solving abilities.
What are some resources to learn more about dynamic programming?
There are plenty of resources available to deepen your understanding of dynamic programming, including online courses, textbooks, and tutorials. Websites like LeetCode, GeeksforGeeks, and CodeSignal offer practice problems and explanations related to dynamic programming. Additionally, joining online coding communities and forums can provide valuable insights and tips from experienced programmers in the field.
You Might Also Like
Binary decision diagrams: simplifying complex decision processes, optimizing data search in binary search trees, binary search tree: structure, operations, and applications, binary tree search: navigating trees for efficient data retrieval, searching in a binary search tree: algorithms and efficiency.
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Latest Posts

Cutting-Edge Artificial Intelligence Project Unveiled in Machine Learning World

Enhancing Exams with Image Processing: E-Assessment Project

Cutting-Edge Blockchain Projects for Cryptocurrency Enthusiasts – Project

Artificial Intelligence Marvel: Cutting-Edge Machine Learning Project

Personalized Affective Feedback Project: Deep Learning Solutions for Student Frustration in IT
Privacy overview.
Sign in to your account
Username or Email Address
Remember Me
- Stack Overflow Public questions & answers
- Stack Overflow for Teams Where developers & technologists share private knowledge with coworkers
- Talent Build your employer brand
- Advertising Reach developers & technologists worldwide
- Labs The future of collective knowledge sharing
- About the company
Collectives™ on Stack Overflow
Find centralized, trusted content and collaborate around the technologies you use most.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Get early access and see previews of new features.
What is dynamic programming? [closed]
What is dynamic programming ?
How is it different from recursion, memoization, etc?
I have read the wikipedia article on it, but I still don't really understand it.
- dynamic-programming
- 2 Here is one tutorial by Michael A. Trick from CMU that I found particularly helpful: mat.gsia.cmu.edu/classes/dynamic/dynamic.html It is certainly in addition to all resources others have recommended (all other resources, specially CLR and Kleinberg,Tardos are very good!). The reason why I like this tutorial is because it introduces advanced concepts fairly gradually. It is bit oldish material but it is a good addition to the list of resources presented here. Also check out Steven Skiena's page and lectures on Dynamic Programming: cs.sunysb.edu/~algorith/video-lectures http: – Edmon Commented Aug 1, 2012 at 13:57
- 12 I have always found "Dynamic Programming" a confusing term - "Dynamic" suggests not-static, but what's "Static Programming"? And "... Programming" brings to mind "Object Oriented Programming" and "Functional Programming", suggesting DP is a programming paradigm. I don't really have a better name (perhaps "Dynamic Algorithms"?) but it's too bad we're stuck with this one. – dimo414 Commented Apr 24, 2015 at 17:07
- 5 @dimo414 The "programming" here is more related to "linear programming" which falls under a class of mathematical optimization methods. See article Mathematical optimization for a list of other mathematical programming methods. – syockit Commented Jun 28, 2016 at 16:10
- 1 @dimo414 "Programming" in this context refers to a tabular method, not to writing computer code. - Coreman – user2618142 Commented Sep 27, 2016 at 7:17
- The bus ticket cost minimization problem described in cs.stackexchange.com/questions/59797/… is best solved in dynamic programming. – daparic Commented May 16, 2019 at 11:06
10 Answers 10
Dynamic programming is when you use past knowledge to make solving a future problem easier.
A good example is solving the Fibonacci sequence for n=1,000,002.
This will be a very long process, but what if I give you the results for n=1,000,000 and n=1,000,001? Suddenly the problem just became more manageable.
Dynamic programming is used a lot in string problems, such as the string edit problem. You solve a subset(s) of the problem and then use that information to solve the more difficult original problem.
With dynamic programming, you store your results in some sort of table generally. When you need the answer to a problem, you reference the table and see if you already know what it is. If not, you use the data in your table to give yourself a stepping stone towards the answer.
The Cormen Algorithms book has a great chapter about dynamic programming. AND it's free on Google Books! Check it out here.
- 55 Didn't you just describe memoization though? – dreadwail Commented Jun 30, 2009 at 19:20
- 33 I would say memoization is a form of dynamic programming, when the memoized function/method is a recursive one. – Daniel Huckstep Commented Jun 30, 2009 at 19:31
- 6 Good answer, would only add a mention about optimal sub-structure (e.g., every subset of any path along the shortest path from A to B is itself the shortest path between the 2 endpoints assuming a distance metric that observes the triangle inequality). – Shea Commented Jun 30, 2009 at 19:56
- 6 I wouldn't say "easier", but faster. A common misunderstanding is that dp solves problems that naive algorithms can't and that isn't the case. Is not a matter of functionality but of performance. – andandandand Commented Jun 30, 2009 at 21:02
- 6 Using memoization, dynamic programming problems can be solved in a top down manner. i.e. calling the function to calculate the final value, and that function in turn calls it self recursively to solve the subproblems. Without it, dynamic programming problems can only be solved in a bottom up way. – Pranav Commented Jul 3, 2009 at 5:51
Dynamic programming is a technique used to avoid computing multiple times the same subproblem in a recursive algorithm.
Let's take the simple example of the Fibonacci numbers: finding the n th Fibonacci number defined by
F n = F n-1 + F n-2 and F 0 = 0, F 1 = 1
The obvious way to do this is recursive:
Dynamic Programming
- Top Down - Memoization
The recursion does a lot of unnecessary calculations because a given Fibonacci number will be calculated multiple times. An easy way to improve this is to cache the results:
A better way to do this is to get rid of the recursion all-together by evaluating the results in the right order:
We can even use constant space and store only the necessary partial results along the way:
How apply dynamic programming?
- Find the recursion in the problem.
- Top-down: store the answer for each subproblem in a table to avoid having to recompute them.
- Bottom-up: Find the right order to evaluate the results so that partial results are available when needed.
Dynamic programming generally works for problems that have an inherent left to right order such as strings, trees or integer sequences. If the naive recursive algorithm does not compute the same subproblem multiple times, dynamic programming won't help.
I made a collection of problems to help understand the logic: https://github.com/tristanguigue/dynamic-programing
- Just out of curiosity to clarify things - in your opinion, a recursive implementation using a recurrence relation and memoization is dynamic programming? – Codor Commented Apr 28, 2017 at 8:27
- Thanks for the explanation. Is there a condition missing from the bottom up : if n in cache as with the top down example or am I missing something. – DavidC Commented Jan 29, 2019 at 11:32
- Do i understand correctly then that any loop where the values computed at each iteration are used in subsequent iterations is an example of dynamic programming? – Alexey Commented Apr 12, 2019 at 9:39
- Could you give any references for the interpretation you gave, including the top-down and bottom-up special cases? – Alexey Commented Apr 12, 2019 at 9:40
Memoization is the when you store previous results of a function call (a real function always returns the same thing, given the same inputs). It doesn't make a difference for algorithmic complexity before the results are stored.
Recursion is the method of a function calling itself, usually with a smaller dataset. Since most recursive functions can be converted to similar iterative functions, this doesn't make a difference for algorithmic complexity either.
Dynamic programming is the process of solving easier-to-solve sub-problems and building up the answer from that. Most DP algorithms will be in the running times between a Greedy algorithm (if one exists) and an exponential (enumerate all possibilities and find the best one) algorithm.
- DP algorithms could be implemented with recursion, but they don't have to be.
- DP algorithms can't be sped up by memoization, since each sub-problem is only ever solved (or the "solve" function called) once.
- "DP algorithms can't be sped up by memoization" I would say this was incorrect. Each sub-problem (function) can be called many thousands of times, so if you can short-circuit that with memoization, then the speed of the overall algorithm is sped up – Steve Dunn Commented Feb 13, 2021 at 14:11
It's an optimization of your algorithm that cuts running time.
While a Greedy Algorithm is usually called naive , because it may run multiple times over the same set of data, Dynamic Programming avoids this pitfall through a deeper understanding of the partial results that must be stored to help build the final solution.
A simple example is traversing a tree or a graph only through the nodes that would contribute with the solution, or putting into a table the solutions that you've found so far so you can avoid traversing the same nodes over and over.
Here's an example of a problem that's suited for dynamic programming, from UVA's online judge: Edit Steps Ladder.
I'm going to make quick briefing of the important part of this problem's analysis, taken from the book Programming Challenges, I suggest you check it out.
Take a good look at that problem, if we define a cost function telling us how far appart two strings are, we have two consider the three natural types of changes: Substitution - change a single character from pattern "s" to a different character in text "t", such as changing "shot" to "spot". Insertion - insert a single character into pattern "s" to help it match text "t", such as changing "ago" to "agog". Deletion - delete a single character from pattern "s" to help it match text "t", such as changing "hour" to "our". When we set each of this operations to cost one step we define the edit distance between two strings. So how do we compute it? We can define a recursive algorithm using the observation that the last character in the string must be either matched, substituted, inserted or deleted. Chopping off the characters in the last edit operation leaves a pair operation leaves a pair of smaller strings. Let i and j be the last character of the relevant prefix of and t, respectively. there are three pairs of shorter strings after the last operation, corresponding to the string after a match/substitution, insertion or deletion. If we knew the cost of editing the three pairs of smaller strings, we could decide which option leads to the best solution and choose that option accordingly. We can learn this cost, through the awesome thing that's recursion: #define MATCH 0 /* enumerated type symbol for match */ #define INSERT 1 /* enumerated type symbol for insert */ #define DELETE 2 /* enumerated type symbol for delete */ int string_compare(char *s, char *t, int i, int j) { int k; /* counter */ int opt[3]; /* cost of the three options */ int lowest_cost; /* lowest cost */ if (i == 0) return(j * indel(’ ’)); if (j == 0) return(i * indel(’ ’)); opt[MATCH] = string_compare(s,t,i-1,j-1) + match(s[i],t[j]); opt[INSERT] = string_compare(s,t,i,j-1) + indel(t[j]); opt[DELETE] = string_compare(s,t,i-1,j) + indel(s[i]); lowest_cost = opt[MATCH]; for (k=INSERT; k<=DELETE; k++) if (opt[k] < lowest_cost) lowest_cost = opt[k]; return( lowest_cost ); } This algorithm is correct, but is also impossibly slow. Running on our computer, it takes several seconds to compare two 11-character strings, and the computation disappears into never-never land on anything longer. Why is the algorithm so slow? It takes exponential time because it recomputes values again and again and again. At every position in the string, the recursion branches three ways, meaning it grows at a rate of at least 3^n – indeed, even faster since most of the calls reduce only one of the two indices, not both of them. So how can we make the algorithm practical? The important observation is that most of these recursive calls are computing things that have already been computed before. How do we know? Well, there can only be |s| · |t| possible unique recursive calls, since there are only that many distinct (i, j) pairs to serve as the parameters of recursive calls. By storing the values for each of these (i, j) pairs in a table, we can avoid recomputing them and just look them up as needed. The table is a two-dimensional matrix m where each of the |s|·|t| cells contains the cost of the optimal solution of this subproblem, as well as a parent pointer explaining how we got to this location: typedef struct { int cost; /* cost of reaching this cell */ int parent; /* parent cell */ } cell; cell m[MAXLEN+1][MAXLEN+1]; /* dynamic programming table */ The dynamic programming version has three differences from the recursive version. First, it gets its intermediate values using table lookup instead of recursive calls. **Second,**it updates the parent field of each cell, which will enable us to reconstruct the edit sequence later. **Third,**Third, it is instrumented using a more general goal cell() function instead of just returning m[|s|][|t|].cost. This will enable us to apply this routine to a wider class of problems.
Here, a very particular analysis of what it takes to gather the most optimal partial results, is what makes the solution a "dynamic" one.
Here's an alternate, full solution to the same problem. It's also a "dynamic" one even though its execution is different. I suggest you check out how efficient the solution is by submitting it to UVA's online judge. I find amazing how such a heavy problem was tackled so efficiently.
- Is storage really required to be dynamic programming? Wouldn't any amount of work skipping qualify an algorithm as dynamic? – Nthalk Commented Oct 21, 2011 at 3:59
- You have to gather optimal step by step results to make an algorithm "dynamic". Dynamic Programming stems from Bellman's work in OR, if you say "that skipping any amount of word is dynamic programming" you're devaluing the term, as any search heuristic would be dynamic programming. en.wikipedia.org/wiki/Dynamic_programming – andandandand Commented Jan 30, 2012 at 0:05
The key bits of dynamic programming are "overlapping sub-problems" and "optimal substructure". These properties of a problem mean that an optimal solution is composed of the optimal solutions to its sub-problems. For instance, shortest path problems exhibit optimal substructure. The shortest path from A to C is the shortest path from A to some node B followed by the shortest path from that node B to C.
In greater detail, to solve a shortest-path problem you will:
- find the distances from the starting node to every node touching it (say from A to B and C)
- find the distances from those nodes to the nodes touching them (from B to D and E, and from C to E and F)
- we now know the shortest path from A to E: it is the shortest sum of A-x and x-E for some node x that we have visited (either B or C)
- repeat this process until we reach the final destination node
Because we are working bottom-up, we already have solutions to the sub-problems when it comes time to use them, by memoizing them.
Remember, dynamic programming problems must have both overlapping sub-problems, and optimal substructure. Generating the Fibonacci sequence is not a dynamic programming problem; it utilizes memoization because it has overlapping sub-problems, but it does not have optimal substructure (because there is no optimization problem involved).
- but it (Fibonacci sequence) does not have optimal substructure I think Fibonacci does have an optimal sub-structure. As I view it, it is basically being able to derive a result using some other results that we already have calculated. In case of Fibonacci, Fib(n) = Fib(n-1) + Fib(n-2) , so isn't this an optimal sub-structure? – Floatoss Commented Mar 25 at 8:39
Dynamic programming (DP) is a general algorithm design technique for solving problems with overlapping sub-problems. This technique was invented by American mathematician “Richard Bellman” in 1950s.
The key idea is to save answers of overlapping smaller sub-problems to avoid recomputation.
Dynamic Programming Properties
- An instance is solved using the solutions for smaller instances.
- The solutions for a smaller instance might be needed multiple times, so store their results in a table.
- Thus each smaller instance is solved only once.
- Additional space is used to save time.
I am also very much new to Dynamic Programming (a powerful algorithm for particular type of problems)
In most simple words, just think dynamic programming as a recursive approach with using the previous knowledge
Previous knowledge is what matters here the most, Keep track of the solution of the sub-problems you already have.
Consider this, most basic example for dp from Wikipedia
Finding the fibonacci sequence
Lets break down the function call with say n = 5
In particular, fib(2) was calculated three times from scratch. In larger examples, many more values of fib, or sub-problems, are recalculated, leading to an exponential time algorithm.
Now, lets try it by storing the value we already found out in a data-structure say a Map
Here we are saving the solution of sub-problems in the map, if we don't have it already. This technique of saving values which we already had calculated is termed as Memoization.
At last, For a problem, first try to find the states (possible sub-problems and try to think of the better recursion approach so that you can use the solution of previous sub-problem into further ones).
- Straight rip-off from Wikipedia. Downvoted!! – solidak Commented Jan 13, 2018 at 13:03
Dynamic programming is a technique for solving problems with overlapping sub problems. A dynamic programming algorithm solves every sub problem just once and then Saves its answer in a table (array). Avoiding the work of re-computing the answer every time the sub problem is encountered. The underlying idea of dynamic programming is: Avoid calculating the same stuff twice, usually by keeping a table of known results of sub problems.
The seven steps in the development of a dynamic programming algorithm are as follows:
- Establish a recursive property that gives the solution to an instance of the problem.
- Develop a recursive algorithm as per recursive property
- See if same instance of the problem is being solved again an again in recursive calls
- Develop a memoized recursive algorithm
- See the pattern in storing the data in the memory
- Convert the memoized recursive algorithm into iterative algorithm
- Optimize the iterative algorithm by using the storage as required (storage optimization)
- Is 6. Convert the memoized recursive algorithm into iterative algorithm a mandatory step? This would mean that its final form is non-recursive? – daparic Commented May 16, 2019 at 11:02
- not its not mandatory, its optional – Adnan Qureshi Commented May 18, 2019 at 19:10
- The objective is to replace the recursive algorithm used to store the data in memory with an iteration over the stored values because an iterative solution saves the creation of a function stack for every recursive call made. – David C. Rankin Commented Jul 25, 2019 at 19:51
in short the difference between recursion memoization and Dynamic programming
Dynamic programming as name suggest is using the previous calculated value to dynamically construct the next new solution
Where to apply dynamic programming : If you solution is based on optimal substructure and overlapping sub problem then in that case using the earlier calculated value will be useful so you do not have to recompute it. It is bottom up approach. Suppose you need to calculate fib(n) in that case all you need to do is add the previous calculated value of fib(n-1) and fib(n-2)
Recursion : Basically subdividing you problem into smaller part to solve it with ease but keep it in mind it does not avoid re computation if we have same value calculated previously in other recursion call.
Memoization : Basically storing the old calculated recursion value in table is known as memoization which will avoid re-computation if its already been calculated by some previous call so any value will be calculated once. So before calculating we check whether this value has already been calculated or not if already calculated then we return the same from table instead of recomputing. It is also top down approach
Here is a simple python code example of Recursive , Top-down , Bottom-up approach for Fibonacci series:
Recursive: O(2 n )
Top-down: o(n) efficient for larger input, bottom-up: o(n) for simplicity and small input sizes.
- Featured on Meta
- Upcoming sign-up experiments related to tags
- The return of Staging Ground to Stack Overflow
- Policy: Generative AI (e.g., ChatGPT) is banned
Hot Network Questions
- How can I permute pair of elements in a list?
- Ideal test/p-value calculation for difference in means with small sample size and right skewed data?
- Were there 3D accelerators built on discrete logic?
- If electromagnetic waves are indeed created by a changing electric and magnetic field, then why don't we see magnet based antennas?
- Are there any precautions I should take if I plan on storing something very heavy near my foundation?
- How do you tell if you're in a nebula?
- How to Create a Fully Centered and Adjustable Multiline Table in LaTeX?
- Should I practise a piece at a metronome tempo that is faster than required?
- Can a prone player character use a disengage action in DnD 5e?
- Trouble with QGIS .shp files and .dbf files
- Would you be able to look directly at the Sun if it were a red giant?
- Tool Storage Corrosion Risk
- How to see image size in Firefox?
- select() / poll() timeout stretches on Linux
- Does every proof need an axiom saying it works?
- Why is "Colourless green ideas sleep furiously" considered meaningless?
- Practical Combat Pipe
- Why do some GA aircraft need weights on the control surfaces?
- How much time is needed to judge an Earth-like planet to be safe?
- Numbers that are 4 times their reverse
- How to temporarily disable a primary IP without losing other IPs on the same interface
- Issue with building a version of Blender 4.1.1 (GooEngine)
- A short story about an ancient anaerobic civilisation on Earth
- Conditions for using Fubini’s Theorem in this problem
- Interview Problems on DP
- Practice DP
- Tutorial on Dynamic Programming
- Optimal Substructure
- Overlapping Subproblem
- Memoization
- Tabulation vs Memoization
- 0/1 Knapsack
- Unbounded Knapsack
- Coin Change
- Egg Dropping Puzzle
- Matrix Chain Multiplication
- Palindrome Partitioning
- DP on Arrays
- DP with Bitmasking
- DP on Trees
- DP on Graph
How Does Dynamic Programming Work?
- Dynamic Programming or DP
- Dynamic Programming (DP) on Grids
- Dynamic Programming (DP) on Arrays Tutorial
- Dynamic Programming meaning in DSA
- Dynamic Programming (DP) Tutorial with Problems
- Do-While loop in Programming
- Dynamic Programming vs Divide-and-Conquer
- Greedy Approach vs Dynamic programming
- How do Dynamic arrays work?
- Introduction to Dynamic Programming on Trees
- Steps for how to solve a Dynamic Programming Problem
- Top 20 Dynamic Programming Interview Questions
- C/C++ Dynamic Programming Programs
- Dynamic Scoping in R Programming
- Algorithms | Dynamic Programming | Question 4
- Algorithms | Dynamic Programming | Question 3
- Algorithms | Dynamic Programming | Question 2
- Algorithms | Dynamic Programming | Question 7
- Algorithms Quiz | Dynamic Programming | Question 8
Dynamic programming, popularly known as DP, is a method of solving problems by breaking them down into simple, overlapping subproblems and then solving each of the subproblems only once, storing the solutions to the subproblems that are solved to avoid redundant computations. This technique is useful for optimization-based problems, where the goal is to find the most optimal solution among all possible set of solutions.
Table of Content
What is Dynamic Programming?
Dynamic programming characteristics.
- Techniques to solve Dynamic Programming Problems
- Understanding Dynamic Programming With Examples
Dynamic Programming is a problem-solving technique used to solve complex problems by breaking them into smaller overlapping subproblems and solving each subproblem only once, storing the solutions to avoid redundant computations. It often involves optimal substructure and overlapping subproblems to efficiently solve problems with recursive structures.
This approach is like the divide and conquers algorithm where a problem is divided into sub-problems and recursively solving sub-problems and combining their solution to find the solution to the original problem.
Dynamic programming is a way of solving tricky problems by breaking them into smaller pieces and solving each piece just once, saving the answers to avoid doing the same work over and over.
Here are two key things to check if dynamic programming is the right tool for the job:
1. Optimal Substructure:
- The problem should have optimal substructure , meaning the best solution comes from combining optimal solutions to smaller sub-problems.
- Take the Fibonacci series as an example, where the nth number is the sum of the previous two numbers: Fib(n) = Fib(n-1) + Fib(n-2).
- This shows how a problem of size “ n ” can be broken down into sub-problems of size “ n-1 ” and “ n-2 ,” helping define the base cases of the recursive algorithm (e.g., f(0) = 0, f(1) = 1).
2. Overlapping Subproblems:
- The other essential characteristic is overlapping subproblems , where the same smaller problems occur repeatedly in a recursive manner.
- By recognizing and storing the solutions to these overlapping subproblems, algorithm performance can be significantly improved.
- In the Fibonacci dynamic programming example, the tree representation reveals that sub-problems like fib(4), fib(3), fib(2), etc., appear multiple times.
- Remember, for a problem to be a good fit for dynamic programming, it needs both optimal substructure and overlapping subproblems.
Techniques to solve Dynamic Programming Problems:
1. top-down(memoization):.
Break down the given problem in order to begin solving it. If you see that the problem has already been solved, return the saved answer. If it hasn’t been solved, solve it and save it. This is usually easy to think of and very intuitive, This is referred to as Memoization .
2. Bottom-Up(Dynamic Programming):
Analyze the problem and see in what order the subproblems are solved, and work your way up from the trivial subproblem to the given problem. This process ensures that the subproblems are solved before the main problem. This is referred to as Bottom-up Dynamic Programming .
Types of the approach of dynamic programming algorithm
Understanding Dynamic Programming With Examples:
Problem: Let’s find the Fibonacci sequence up to the nth term . A Fibonacci series is the sequence of numbers in which each number is the sum of the two preceding ones. For example, 0, 1, 1, 2, 3, and so on. Here, each number is the sum of the two preceding numbers.
Naive Approach: The basic way to find the nth Fibonacci number is to use recursion.
Below is the implementation for the above approach:
Complexity Analysis:
- Here, for every n, we are required to make a recursive call to fib(n – 1) and fib(n – 2). For fib(n – 1), we will again make the recursive call to fib(n – 2) and fib(n – 3). Similarly, for fib(n – 2), recursive calls are made on fib(n – 3) and fib(n – 4) until we reach the base case.
- During each recursive call, we perform constant work(k) (adding previous outputs to obtain the current output). We perform 2nK work at every level (where n = 0, 1, 2, …). Since n is the number of calls needed to reach 1, we are performing 2n-1k at the final level. Total work can be calculated as:
- If we draw the recursion tree of the Fibonacci recursion then we found the maximum height of the tree will be n and hence the space complexity of the Fibonacci recursion will be O(n).
Efficient approach: As it is a very terrible complexity(Exponential), thus we need to optimize it with an efficient method. ( Memoization )
Let’s look at the example below for finding the 5th Fibonacci number.
Observations:
The entire program repeats recursive calls. As in the above figure, for calculating fib(4) , we need the value of fib(3) (first recursive call over f ib(3) ), and for calculating fib(5) , we again need the value of fib(3)(second similar recursive call over fib(3) ). Both of these recursive calls are shown above in the outlining circle. Similarly, there are many others for which we are repeating the recursive calls. Recursion generally involves repeated recursive calls, which increases the program’s time complexity. By storing the output of previously encountered values (preferably in arrays, as these can be traversed and extracted most efficiently), we can overcome this problem. The next time we make a recursive call over these values, we will use their already stored outputs instead of calculating them all over again. In this way, we can improve the performance of our code. Memoization is the process of storing each recursive call’s output for later use, preventing the code from calculating it again. Way to memoize: To achieve this in our example we will simply take an answer array initialized to -1. As we make a recursive call, we will first check if the value stored in the answer array corresponding to that position is -1. The value -1 indicates that we haven’t calculated it yet and have to recursively compute it. The output must be stored in the answer array so that, next time, if the same value is encountered, it can be directly used from the answer array. Now in this process of memoization, considering the above Fibonacci numbers example, it can be observed that the total number of unique calls will be at most (n + 1) only.
Time complexity: O(n) Auxiliary Space: O(n)
Optimized approach: Following a bottom-up approach to reach the desired index. This approach of converting recursion into iteration is known as Bottom up-Dynamic programming(DP) .
Finally, what we do is recursively call each response index field and calculate its value using previously saved outputs. Recursive calls terminate via the base case, which means we are already aware of the answers which should be stored in the base case indexes. In the case of Fibonacci numbers , these indices are 0 and 1 as f(ib0) = 0 and f(ib1) = 1 . So we can directly assign these two values into our answer array and then use them to calculate f(ib2), which is f(ib1) + f(ib0), and so on for each subsequent index. This can easily be done iteratively by running a loop from i = (2 to n). Finally, we get our answer at the 5th index of the array because we already know that the ith index contains the answer to the ith value. Simply, we first try to find out the dependence of the current value on previous values and then use them to calculate our new value. Now, we are looking for those values which do not depend on other values, which means they are independent(base case values, since these, are the smallest problems which we are already aware of).
Dynamic programming , also known as DP , is a problem-solving technique that is very powerful. It breaks complex problems into simpler, overlapping subproblems and then, one by one, solves each problem. Memorization and tabulation are two approaches to implementing dynamic programming. Memorization , a top-bottom approach, optimises recursive solutions by storing results in a memo table. Tabulation , a bottom-up approach, builds solutions through an iterative approach and provides an efficient alternative. Both techniques enhance algorithm efficiency, as demonstrated in the Fibonacci numbers example, optimizing time and space complexities.
Please Login to comment...
Similar reads.
- Geeks Premier League 2023
- Dynamic Programming
- Geeks Premier League
Improve your Coding Skills with Practice
What kind of Experience do you want to share?

- Interview Q
DAA Tutorial
Asymptotic analysis, analysis of sorting, divide and conquer, lower bound theory, sorting in linear time, binary search trees, red black tree, dynamic programming, greedy algorithm, backtracking, shortest path, all-pairs shortest paths, maximum flow, sorting networks, complexity theory, approximation algo, string matching.
Interview Questions








IMAGES
VIDEO
COMMENTS
Dynamic Programming (DP) is a method used in mathematics and computer science to solve complex problems by breaking them down into simpler subproblems. By solving each subproblem only once and storing the results, it avoids redundant computations, leading to more efficient solutions for a wide range of problems.
Dynamic programming refers to a problem-solving approach, in which we precompute and store simpler, similar subproblems, in order to build up the solution to a complex problem. It is similar to recursion, in which calculating the base cases allows us to inductively determine the final value. This bottom-up approach works well when the new value depends only on previously calculated values.
Dynamic programming is a problem-solving technique that has gained significant attention in the world of computer science. It is a concept that is often used in technical interviews to test a ...
In general, dynamic programming (DP) is one of the most powerful techniques for solving a certain class of problems. There is an elegant way to formulate the approach and a very simple thinking process, and the coding part is very easy. Essentially, it is a simple idea, after solving a problem with a given input, save the result as a reference ...
What Is Dynamic Programming? Simply put, dynamic programming is an optimization method for recursive algorithms, most of which are used to solve computing or mathematical problems. You can also call it an algorithmic technique for solving an optimization problem by breaking it into simpler sub-problems.
Step 3: Formulating a relation among the states. This part is the hardest part of solving a Dynamic Programming problem and requires a lot of intuition, observation, and practice. Example: Given 3 numbers {1, 3, 5}, The task is to tell the total number of ways we can form a number N using the sum of the given three numbers. (allowing ...
The dynamic programming approach to solve this problem involves breaking it apart into a sequence of smaller decisions. To do so, we define a sequence of value functions (), for =,,, …,, + which represent the value of having any amount of capital k at each time t.
Dynamic programming is a problem-solving paradigm used to find a solution by breaking the larger problem into subproblems. This approach takes advantage of the fact that the optimal solution to a problem depends upon the optimal solution to its subproblems. But dynamic programming isn't the right approach for every problem.
Dynamic programming. Dynamic programming is an efficient method for solving computing problems by saving solutions in memory for future reference. When you have overlapping subproblems, you can apply dynamic programming to save time and increase program efficiency. More From Artturi Jalli: Python Cheat Sheet: A Handy Guide to Python.
Thought first by Richard Bellman in the 1950s, Dynamic Programming (DP) is a problem-solving technique used in computer science and mathematics to solve complex larger problems by breaking them down into simpler, smaller overlapping subproblems. The key idea is solving each subproblem once and storing the results to avoid redundant calculations.
Dynamic Programming is a technique in computer programming that helps to efficiently solve a class of problems that have overlapping subproblems and optimal substructure property.. If any problem can be divided into subproblems, which in turn are divided into smaller subproblems, and if there are overlapping among these subproblems, then the solutions to these subproblems can be saved for ...
Dynamic programming is a technique of breaking down a problem into smaller problems, solving each sub-problems once, storing the solutions of these sub-problems, and eventually finding a solution to the original problem. We break down a big problem into smaller problems. Typically, the smaller problems are similar to the parent problem only ...
1. Find the First Solution. The first step for any dynamic programming problem (and the step that most people skip) is to find an initial brute-force solution to the problem. The goal here is to just get something down on paper without any concern for efficiency.
Dynamic programming is a technique used to solve problems by dividing them into simpler, overlapping subproblems and combining their solutions to construct the optimal solution. It is based on the idea of recursion, where a problem is solved by breaking it down into smaller instances of the same problem.
Step 1: How to recognize a Dynamic Programming problem. First, let's make it clear that DP is essentially just an optimization technique. DP is a method for solving problems by breaking them down into a collection of simpler subproblems, solving each of those subproblems just once, and storing their solutions.
Understanding Dynamic Programming can help you solve complex programming problems faster. These methods can help you ace programming interview questions about data structures and algorithms. And they can improve your day-to-day coding as well. We released a 5-hour course on Dynamic Programming on the freeCodeCamp.org YouTube channel.
Dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It involves solving each subproblem only once and storing the solution to avoid redundant calculations. This approach can significantly improve the efficiency of solving problems with overlapping subproblems.
Dynamic programming is a technique for solving problems with overlapping sub problems. A dynamic programming algorithm solves every sub problem just once and then Saves its answer in a table (array). Avoiding the work of re-computing the answer every time the sub problem is encountered.
Here are a few reasons why dynamic programming is so important: 1. **Efficiency**: Dynamic programming can significantly reduce the time and space complexity of solving complex problems, making it ...
Dynamic programming, also known as DP, is a problem-solving technique that is very powerful. It breaks complex problems into simpler, overlapping subproblems and then, one by one, solves each problem. Memorization and tabulation are two approaches to implementing dynamic programming. Memorization, a top-bottom approach, optimises recursive ...
To solve any dynamic programming problem, we can use the FAST method. Here, FAST stands for: 'F' stands for Find the recursive solution: Whenever we find any DP problem, we have to find the recursive solution. 'A' stands for Analyse the solution: Once we find the recursive solution then we have to analyse the solution and look for the ...
Dynamic problems in computational complexity theory are problems stated in terms of changing input data. In its most general form, a problem in this category is usually stated as follows: Given a class of input objects, find efficient algorithms and data structures to answer a certain query about a set of input objects each time the input data is modified, i.e., objects are inserted or deleted.
Dynamic programming is more efficient than Divide and conquer technique. Divide and conquer strategy is less efficient than the dynamic programming because we have to rework the solutions. It is the non-recursive approach. It is a recursive approach. It uses the bottom-up approach of problem- solving.
In this paper, several efficient dynamic programming-based algorithms are designed to solve the problem. First, a dynamic programming model is established for the deterministic version of the problem, and the optimal solution can be obtained by the dynamic programming approach. Furthermore, faced with the uncertainty introduced by sampling ...
In the dynamic world of brand strategy, solving problems with a dash of creativity isn't just beneficial—it's necessary. Your brand's ability to stand out in a saturated market hinges on ...
Problem-solving strategies can be enhanced with the application of creative techniques. You can use creativity to: Approach problems from different angles. Improve your problem-solving process. Spark creativity in your employees and peers. 6. Adaptability. Adaptability is the capacity to adjust to change. When a particular solution to an issue ...
We introduce Mathador-LM, a new benchmark for evaluating the mathematical reasoning on large language models (LLMs), combining ruleset interpretation, planning, and problem-solving. This benchmark is inspired by the Mathador game, where the objective is to reach a target number using basic arithmetic operations on a given set of base numbers, following a simple set of rules. We show that ...
Differential evolution algorithm with dynamic population scheme Differential evolution DE is an efficient population-based evolutionary algorithm for solving optimisation problems. Its control parameters have significant influence on performance.