9.1 Null and Alternative Hypotheses
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.
Mathematical Symbols Used in H 0 and H a :
| equal (=) | not equal (≠) greater than (>) less than (<) |
| greater than or equal to (≥) | less than (<) |
| less than or equal to (≤) | more than (>) |
H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1
H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.
Example 9.2
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 66
- H a : μ __ 66
Example 9.3
We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 45
- H a : μ __ 45
Example 9.4
An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066
On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : p __ 0.40
- H a : p __ 0.40
Collaborative Exercise
Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.
Access for free at https://openstax.org/books/statistics/pages/1-introduction
- Authors: Barbara Illowsky, Susan Dean
- Publisher/website: OpenStax
- Book title: Statistics
- Publication date: Mar 27, 2020
- Location: Houston, Texas
- Book URL: https://openstax.org/books/statistics/pages/1-introduction
- Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses
© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
Hypothesis Testing
About hypothesis testing.
Contents (Click to skip to the section):
What is a Hypothesis?
What is hypothesis testing.
- Hypothesis Testing Examples (One Sample Z Test).
- Hypothesis Test on a Mean (TI 83).
Bayesian Hypothesis Testing.
- More Hypothesis Testing Articles
- Hypothesis Tests in One Picture
- Critical Values
What is the Null Hypothesis?
Need help with a homework problem? Check out our tutoring page!

A hypothesis is an educated guess about something in the world around you. It should be testable, either by experiment or observation. For example:
- A new medicine you think might work.
- A way of teaching you think might be better.
- A possible location of new species.
- A fairer way to administer standardized tests.
It can really be anything at all as long as you can put it to the test.
What is a Hypothesis Statement?
If you are going to propose a hypothesis, it’s customary to write a statement. Your statement will look like this: “If I…(do this to an independent variable )….then (this will happen to the dependent variable ).” For example:
- If I (decrease the amount of water given to herbs) then (the herbs will increase in size).
- If I (give patients counseling in addition to medication) then (their overall depression scale will decrease).
- If I (give exams at noon instead of 7) then (student test scores will improve).
- If I (look in this certain location) then (I am more likely to find new species).
A good hypothesis statement should:
- Include an “if” and “then” statement (according to the University of California).
- Include both the independent and dependent variables.
- Be testable by experiment, survey or other scientifically sound technique.
- Be based on information in prior research (either yours or someone else’s).
- Have design criteria (for engineering or programming projects).
Hypothesis testing can be one of the most confusing aspects for students, mostly because before you can even perform a test, you have to know what your null hypothesis is. Often, those tricky word problems that you are faced with can be difficult to decipher. But it’s easier than you think; all you need to do is:
- Figure out your null hypothesis,
- State your null hypothesis,
- Choose what kind of test you need to perform,
- Either support or reject the null hypothesis .
If you trace back the history of science, the null hypothesis is always the accepted fact. Simple examples of null hypotheses that are generally accepted as being true are:
- DNA is shaped like a double helix.
- There are 8 planets in the solar system (excluding Pluto).
- Taking Vioxx can increase your risk of heart problems (a drug now taken off the market).
How do I State the Null Hypothesis?
You won’t be required to actually perform a real experiment or survey in elementary statistics (or even disprove a fact like “Pluto is a planet”!), so you’ll be given word problems from real-life situations. You’ll need to figure out what your hypothesis is from the problem. This can be a little trickier than just figuring out what the accepted fact is. With word problems, you are looking to find a fact that is nullifiable (i.e. something you can reject).
Hypothesis Testing Examples #1: Basic Example
A researcher thinks that if knee surgery patients go to physical therapy twice a week (instead of 3 times), their recovery period will be longer. Average recovery times for knee surgery patients is 8.2 weeks.
The hypothesis statement in this question is that the researcher believes the average recovery time is more than 8.2 weeks. It can be written in mathematical terms as: H 1 : μ > 8.2
Next, you’ll need to state the null hypothesis . That’s what will happen if the researcher is wrong . In the above example, if the researcher is wrong then the recovery time is less than or equal to 8.2 weeks. In math, that’s: H 0 μ ≤ 8.2
Rejecting the null hypothesis
Ten or so years ago, we believed that there were 9 planets in the solar system. Pluto was demoted as a planet in 2006. The null hypothesis of “Pluto is a planet” was replaced by “Pluto is not a planet.” Of course, rejecting the null hypothesis isn’t always that easy— the hard part is usually figuring out what your null hypothesis is in the first place.
Hypothesis Testing Examples (One Sample Z Test)
The one sample z test isn’t used very often (because we rarely know the actual population standard deviation ). However, it’s a good idea to understand how it works as it’s one of the simplest tests you can perform in hypothesis testing. In English class you got to learn the basics (like grammar and spelling) before you could write a story; think of one sample z tests as the foundation for understanding more complex hypothesis testing. This page contains two hypothesis testing examples for one sample z-tests .
One Sample Hypothesis Testing Example: One Tailed Z Test
A principal at a certain school claims that the students in his school are above average intelligence. A random sample of thirty students IQ scores have a mean score of 112.5. Is there sufficient evidence to support the principal’s claim? The mean population IQ is 100 with a standard deviation of 15.
Step 1: State the Null hypothesis . The accepted fact is that the population mean is 100, so: H 0 : μ = 100.
Step 2: State the Alternate Hypothesis . The claim is that the students have above average IQ scores, so: H 1 : μ > 100. The fact that we are looking for scores “greater than” a certain point means that this is a one-tailed test.
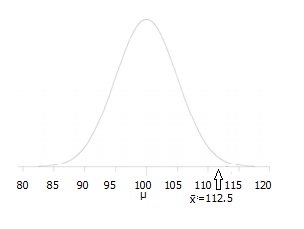
Step 4: State the alpha level . If you aren’t given an alpha level , use 5% (0.05).
Step 5: Find the rejection region area (given by your alpha level above) from the z-table . An area of .05 is equal to a z-score of 1.645.
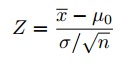
Step 6: If Step 6 is greater than Step 5, reject the null hypothesis. If it’s less than Step 5, you cannot reject the null hypothesis. In this case, it is more (4.56 > 1.645), so you can reject the null.
One Sample Hypothesis Testing Examples: #3
Blood glucose levels for obese patients have a mean of 100 with a standard deviation of 15. A researcher thinks that a diet high in raw cornstarch will have a positive or negative effect on blood glucose levels. A sample of 30 patients who have tried the raw cornstarch diet have a mean glucose level of 140. Test the hypothesis that the raw cornstarch had an effect.
- State the null hypothesis : H 0 :μ=100
- State the alternate hypothesis : H 1 :≠100
- State your alpha level. We’ll use 0.05 for this example. As this is a two-tailed test, split the alpha into two. 0.05/2=0.025
- Find the z-score associated with your alpha level . You’re looking for the area in one tail only . A z-score for 0.75(1-0.025=0.975) is 1.96. As this is a two-tailed test, you would also be considering the left tail (z = 1.96)
- If Step 5 is less than -1.96 or greater than 1.96 (Step 3), reject the null hypothesis . In this case, it is greater, so you can reject the null.
*This process is made much easier if you use a TI-83 or Excel to calculate the z-score (the “critical value”). See:
- Critical z value TI 83
- Z Score in Excel
Hypothesis Testing Examples: Mean (Using TI 83)
You can use the TI 83 calculator for hypothesis testing, but the calculator won’t figure out the null and alternate hypotheses; that’s up to you to read the question and input it into the calculator.
Example problem : A sample of 200 people has a mean age of 21 with a population standard deviation (σ) of 5. Test the hypothesis that the population mean is 18.9 at α = 0.05.
Step 1: State the null hypothesis. In this case, the null hypothesis is that the population mean is 18.9, so we write: H 0 : μ = 18.9
Step 2: State the alternative hypothesis. We want to know if our sample, which has a mean of 21 instead of 18.9, really is different from the population, therefore our alternate hypothesis: H 1 : μ ≠ 18.9
Step 3: Press Stat then press the right arrow twice to select TESTS.
Step 4: Press 1 to select 1:Z-Test… . Press ENTER.
Step 5: Use the right arrow to select Stats .
Step 6: Enter the data from the problem: μ 0 : 18.9 σ: 5 x : 21 n: 200 μ: ≠μ 0
Step 7: Arrow down to Calculate and press ENTER. The calculator shows the p-value: p = 2.87 × 10 -9
This is smaller than our alpha value of .05. That means we should reject the null hypothesis .
Bayesian Hypothesis Testing: What is it?
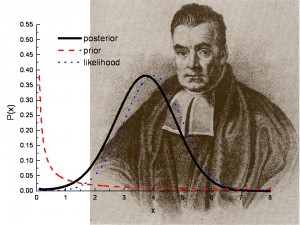
Bayesian hypothesis testing helps to answer the question: Can the results from a test or survey be repeated? Why do we care if a test can be repeated? Let’s say twenty people in the same village came down with leukemia. A group of researchers find that cell-phone towers are to blame. However, a second study found that cell-phone towers had nothing to do with the cancer cluster in the village. In fact, they found that the cancers were completely random. If that sounds impossible, it actually can happen! Clusters of cancer can happen simply by chance . There could be many reasons why the first study was faulty. One of the main reasons could be that they just didn’t take into account that sometimes things happen randomly and we just don’t know why.
It’s good science to let people know if your study results are solid, or if they could have happened by chance. The usual way of doing this is to test your results with a p-value . A p value is a number that you get by running a hypothesis test on your data. A P value of 0.05 (5%) or less is usually enough to claim that your results are repeatable. However, there’s another way to test the validity of your results: Bayesian Hypothesis testing. This type of testing gives you another way to test the strength of your results.
Traditional testing (the type you probably came across in elementary stats or AP stats) is called Non-Bayesian. It is how often an outcome happens over repeated runs of the experiment. It’s an objective view of whether an experiment is repeatable. Bayesian hypothesis testing is a subjective view of the same thing. It takes into account how much faith you have in your results. In other words, would you wager money on the outcome of your experiment?
Differences Between Traditional and Bayesian Hypothesis Testing.
Traditional testing (Non Bayesian) requires you to repeat sampling over and over, while Bayesian testing does not. The main different between the two is in the first step of testing: stating a probability model. In Bayesian testing you add prior knowledge to this step. It also requires use of a posterior probability , which is the conditional probability given to a random event after all the evidence is considered.
Arguments for Bayesian Testing.
Many researchers think that it is a better alternative to traditional testing, because it:
- Includes prior knowledge about the data.
- Takes into account personal beliefs about the results.
Arguments against.
- Including prior data or knowledge isn’t justifiable.
- It is difficult to calculate compared to non-Bayesian testing.
Back to top
Hypothesis Testing Articles
- What is Ad Hoc Testing?
- Composite Hypothesis Test
- What is a Rejection Region?
- What is a Two Tailed Test?
- How to Decide if a Hypothesis Test is a One Tailed Test or a Two Tailed Test.
- How to Decide if a Hypothesis is a Left Tailed Test or a Right-Tailed Test.
- How to State the Null Hypothesis in Statistics.
- How to Find a Critical Value .
- How to Support or Reject a Null Hypothesis.
Specific Tests:
- Brunner Munzel Test (Generalized Wilcoxon Test).
- Chi Square Test for Normality.
- Cochran-Mantel-Haenszel Test.
- Granger Causality Test .
- Hotelling’s T-Squared.
- KPSS Test .
- What is a Likelihood-Ratio Test?
- Log rank test .
- MANCOVA Assumptions.
- MANCOVA Sample Size.
- Marascuilo Procedure
- Rao’s Spacing Test
- Rayleigh test of uniformity.
- Sequential Probability Ratio Test.
- How to Run a Sign Test.
- T Test: one sample.
- T-Test: Two sample .
- Welch’s ANOVA .
- Welch’s Test for Unequal Variances .
- Z-Test: one sample .
- Z Test: Two Proportion.
- Wald Test .
Related Articles:
- What is an Acceptance Region?
- How to Calculate Chebyshev’s Theorem.
- Contrast Analysis
- Decision Rule.
- Degrees of Freedom .
- Directional Test
- False Discovery Rate
- How to calculate the Least Significant Difference.
- Levels in Statistics.
- How to Calculate Margin of Error.
- Mean Difference (Difference in Means)
- The Multiple Testing Problem .
- What is the Neyman-Pearson Lemma?
- What is an Omnibus Test?
- One Sample Median Test .
- How to Find a Sample Size (General Instructions).
- Sig 2(Tailed) meaning in results
- What is a Standardized Test Statistic?
- How to Find Standard Error
- Standardized values: Example.
- How to Calculate a T-Score.
- T-Score Vs. a Z.Score.
- Testing a Single Mean.
- Unequal Sample Sizes.
- Uniformly Most Powerful Tests.
- How to Calculate a Z-Score.
- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive
Null Hypothesis: Definition, Rejecting & Examples
By Jim Frost 6 Comments
What is a Null Hypothesis?
The null hypothesis in statistics states that there is no difference between groups or no relationship between variables. It is one of two mutually exclusive hypotheses about a population in a hypothesis test.

- Null Hypothesis H 0 : No effect exists in the population.
- Alternative Hypothesis H A : The effect exists in the population.
In every study or experiment, researchers assess an effect or relationship. This effect can be the effectiveness of a new drug, building material, or other intervention that has benefits. There is a benefit or connection that the researchers hope to identify. Unfortunately, no effect may exist. In statistics, we call this lack of an effect the null hypothesis. Researchers assume that this notion of no effect is correct until they have enough evidence to suggest otherwise, similar to how a trial presumes innocence.
In this context, the analysts don’t necessarily believe the null hypothesis is correct. In fact, they typically want to reject it because that leads to more exciting finds about an effect or relationship. The new vaccine works!
You can think of it as the default theory that requires sufficiently strong evidence to reject. Like a prosecutor, researchers must collect sufficient evidence to overturn the presumption of no effect. Investigators must work hard to set up a study and a data collection system to obtain evidence that can reject the null hypothesis.
Related post : What is an Effect in Statistics?
Null Hypothesis Examples
Null hypotheses start as research questions that the investigator rephrases as a statement indicating there is no effect or relationship.
| Does the vaccine prevent infections? | The vaccine does not affect the infection rate. |
| Does the new additive increase product strength? | The additive does not affect mean product strength. |
| Does the exercise intervention increase bone mineral density? | The intervention does not affect bone mineral density. |
| As screen time increases, does test performance decrease? | There is no relationship between screen time and test performance. |
After reading these examples, you might think they’re a bit boring and pointless. However, the key is to remember that the null hypothesis defines the condition that the researchers need to discredit before suggesting an effect exists.
Let’s see how you reject the null hypothesis and get to those more exciting findings!
When to Reject the Null Hypothesis
So, you want to reject the null hypothesis, but how and when can you do that? To start, you’ll need to perform a statistical test on your data. The following is an overview of performing a study that uses a hypothesis test.
The first step is to devise a research question and the appropriate null hypothesis. After that, the investigators need to formulate an experimental design and data collection procedures that will allow them to gather data that can answer the research question. Then they collect the data. For more information about designing a scientific study that uses statistics, read my post 5 Steps for Conducting Studies with Statistics .
After data collection is complete, statistics and hypothesis testing enter the picture. Hypothesis testing takes your sample data and evaluates how consistent they are with the null hypothesis. The p-value is a crucial part of the statistical results because it quantifies how strongly the sample data contradict the null hypothesis.
When the sample data provide sufficient evidence, you can reject the null hypothesis. In a hypothesis test, this process involves comparing the p-value to your significance level .
Rejecting the Null Hypothesis
Reject the null hypothesis when the p-value is less than or equal to your significance level. Your sample data favor the alternative hypothesis, which suggests that the effect exists in the population. For a mnemonic device, remember—when the p-value is low, the null must go!
When you can reject the null hypothesis, your results are statistically significant. Learn more about Statistical Significance: Definition & Meaning .
Failing to Reject the Null Hypothesis
Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis. The sample data provides insufficient data to conclude that the effect exists in the population. When the p-value is high, the null must fly!
Note that failing to reject the null is not the same as proving it. For more information about the difference, read my post about Failing to Reject the Null .
That’s a very general look at the process. But I hope you can see how the path to more exciting findings depends on being able to rule out the less exciting null hypothesis that states there’s nothing to see here!
Let’s move on to learning how to write the null hypothesis for different types of effects, relationships, and tests.
Related posts : How Hypothesis Tests Work and Interpreting P-values
How to Write a Null Hypothesis
The null hypothesis varies by the type of statistic and hypothesis test. Remember that inferential statistics use samples to draw conclusions about populations. Consequently, when you write a null hypothesis, it must make a claim about the relevant population parameter . Further, that claim usually indicates that the effect does not exist in the population. Below are typical examples of writing a null hypothesis for various parameters and hypothesis tests.
Related posts : Descriptive vs. Inferential Statistics and Populations, Parameters, and Samples in Inferential Statistics
Group Means
T-tests and ANOVA assess the differences between group means. For these tests, the null hypothesis states that there is no difference between group means in the population. In other words, the experimental conditions that define the groups do not affect the mean outcome. Mu (µ) is the population parameter for the mean, and you’ll need to include it in the statement for this type of study.
For example, an experiment compares the mean bone density changes for a new osteoporosis medication. The control group does not receive the medicine, while the treatment group does. The null states that the mean bone density changes for the control and treatment groups are equal.
- Null Hypothesis H 0 : Group means are equal in the population: µ 1 = µ 2 , or µ 1 – µ 2 = 0
- Alternative Hypothesis H A : Group means are not equal in the population: µ 1 ≠ µ 2 , or µ 1 – µ 2 ≠ 0.
Group Proportions
Proportions tests assess the differences between group proportions. For these tests, the null hypothesis states that there is no difference between group proportions. Again, the experimental conditions did not affect the proportion of events in the groups. P is the population proportion parameter that you’ll need to include.
For example, a vaccine experiment compares the infection rate in the treatment group to the control group. The treatment group receives the vaccine, while the control group does not. The null states that the infection rates for the control and treatment groups are equal.
- Null Hypothesis H 0 : Group proportions are equal in the population: p 1 = p 2 .
- Alternative Hypothesis H A : Group proportions are not equal in the population: p 1 ≠ p 2 .
Correlation and Regression Coefficients
Some studies assess the relationship between two continuous variables rather than differences between groups.
In these studies, analysts often use either correlation or regression analysis . For these tests, the null states that there is no relationship between the variables. Specifically, it says that the correlation or regression coefficient is zero. As one variable increases, there is no tendency for the other variable to increase or decrease. Rho (ρ) is the population correlation parameter and beta (β) is the regression coefficient parameter.
For example, a study assesses the relationship between screen time and test performance. The null states that there is no correlation between this pair of variables. As screen time increases, test performance does not tend to increase or decrease.
- Null Hypothesis H 0 : The correlation in the population is zero: ρ = 0.
- Alternative Hypothesis H A : The correlation in the population is not zero: ρ ≠ 0.
For all these cases, the analysts define the hypotheses before the study. After collecting the data, they perform a hypothesis test to determine whether they can reject the null hypothesis.
The preceding examples are all for two-tailed hypothesis tests. To learn about one-tailed tests and how to write a null hypothesis for them, read my post One-Tailed vs. Two-Tailed Tests .
Related post : Understanding Correlation
Neyman, J; Pearson, E. S. (January 1, 1933). On the Problem of the most Efficient Tests of Statistical Hypotheses . Philosophical Transactions of the Royal Society A . 231 (694–706): 289–337.
Share this:

Reader Interactions
January 11, 2024 at 2:57 pm
Thanks for the reply.
January 10, 2024 at 1:23 pm
Hi Jim, In your comment you state that equivalence test null and alternate hypotheses are reversed. For hypothesis tests of data fits to a probability distribution, the null hypothesis is that the probability distribution fits the data. Is this correct?
January 10, 2024 at 2:15 pm
Those two separate things, equivalence testing and normality tests. But, yes, you’re correct for both.
Hypotheses are switched for equivalence testing. You need to “work” (i.e., collect a large sample of good quality data) to be able to reject the null that the groups are different to be able to conclude they’re the same.
With typical hypothesis tests, if you have low quality data and a low sample size, you’ll fail to reject the null that they’re the same, concluding they’re equivalent. But that’s more a statement about the low quality and small sample size than anything to do with the groups being equal.
So, equivalence testing make you work to obtain a finding that the groups are the same (at least within some amount you define as a trivial difference).
For normality testing, and other distribution tests, the null states that the data follow the distribution (normal or whatever). If you reject the null, you have sufficient evidence to conclude that your sample data don’t follow the probability distribution. That’s a rare case where you hope to fail to reject the null. And it suffers from the problem I describe above where you might fail to reject the null simply because you have a small sample size. In that case, you’d conclude the data follow the probability distribution but it’s more that you don’t have enough data for the test to register the deviation. In this scenario, if you had a larger sample size, you’d reject the null and conclude it doesn’t follow that distribution.
I don’t know of any equivalence testing type approach for distribution fit tests where you’d need to work to show the data follow a distribution, although I haven’t looked for one either!
February 20, 2022 at 9:26 pm
Is a null hypothesis regularly (always) stated in the negative? “there is no” or “does not”
February 23, 2022 at 9:21 pm
Typically, the null hypothesis includes an equal sign. The null hypothesis states that the population parameter equals a particular value. That value is usually one that represents no effect. In the case of a one-sided hypothesis test, the null still contains an equal sign but it’s “greater than or equal to” or “less than or equal to.” If you wanted to translate the null hypothesis from its native mathematical expression, you could use the expression “there is no effect.” But the mathematical form more specifically states what it’s testing.
It’s the alternative hypothesis that typically contains does not equal.
There are some exceptions. For example, in an equivalence test where the researchers want to show that two things are equal, the null hypothesis states that they’re not equal.
In short, the null hypothesis states the condition that the researchers hope to reject. They need to work hard to set up an experiment and data collection that’ll gather enough evidence to be able to reject the null condition.
February 15, 2022 at 9:32 am
Dear sir I always read your notes on Research methods.. Kindly tell is there any available Book on all these..wonderfull Urgent
Comments and Questions Cancel reply
Null Hypothesis Examples
ThoughtCo / Hilary Allison
- Scientific Method
- Chemical Laws
- Periodic Table
- Projects & Experiments
- Biochemistry
- Physical Chemistry
- Medical Chemistry
- Chemistry In Everyday Life
- Famous Chemists
- Activities for Kids
- Abbreviations & Acronyms
- Weather & Climate
- Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
- B.A., Physics and Mathematics, Hastings College
In statistical analysis, the null hypothesis assumes there is no meaningful relationship between two variables. Testing the null hypothesis can tell you whether your results are due to the effect of manipulating a dependent variable or due to chance. It's often used in conjunction with an alternative hypothesis, which assumes there is, in fact, a relationship between two variables.
The null hypothesis is among the easiest hypothesis to test using statistical analysis, making it perhaps the most valuable hypothesis for the scientific method. By evaluating a null hypothesis in addition to another hypothesis, researchers can support their conclusions with a higher level of confidence. Below are examples of how you might formulate a null hypothesis to fit certain questions.
What Is the Null Hypothesis?
The null hypothesis states there is no relationship between the measured phenomenon (the dependent variable ) and the independent variable , which is the variable an experimenter typically controls or changes. You do not need to believe that the null hypothesis is true to test it. On the contrary, you will likely suspect there is a relationship between a set of variables. One way to prove that this is the case is to reject the null hypothesis. Rejecting a hypothesis does not mean an experiment was "bad" or that it didn't produce results. In fact, it is often one of the first steps toward further inquiry.
To distinguish it from other hypotheses , the null hypothesis is written as H 0 (which is read as “H-nought,” "H-null," or "H-zero"). A significance test is used to determine the likelihood that the results supporting the null hypothesis are not due to chance. A confidence level of 95% or 99% is common. Keep in mind, even if the confidence level is high, there is still a small chance the null hypothesis is not true, perhaps because the experimenter did not account for a critical factor or because of chance. This is one reason why it's important to repeat experiments.
Examples of the Null Hypothesis
To write a null hypothesis, first start by asking a question. Rephrase that question in a form that assumes no relationship between the variables. In other words, assume a treatment has no effect. Write your hypothesis in a way that reflects this.
| Are teens better at math than adults? | Age has no effect on mathematical ability. |
| Does taking aspirin every day reduce the chance of having a heart attack? | Taking aspirin daily does not affect heart attack risk. |
| Do teens use cell phones to access the internet more than adults? | Age has no effect on how cell phones are used for internet access. |
| Do cats care about the color of their food? | Cats express no food preference based on color. |
| Does chewing willow bark relieve pain? | There is no difference in pain relief after chewing willow bark versus taking a placebo. |
Other Types of Hypotheses
In addition to the null hypothesis, the alternative hypothesis is also a staple in traditional significance tests . It's essentially the opposite of the null hypothesis because it assumes the claim in question is true. For the first item in the table above, for example, an alternative hypothesis might be "Age does have an effect on mathematical ability."
Key Takeaways
- In hypothesis testing, the null hypothesis assumes no relationship between two variables, providing a baseline for statistical analysis.
- Rejecting the null hypothesis suggests there is evidence of a relationship between variables.
- By formulating a null hypothesis, researchers can systematically test assumptions and draw more reliable conclusions from their experiments.
- Difference Between Independent and Dependent Variables
- Examples of Independent and Dependent Variables
- What Is a Hypothesis? (Science)
- What 'Fail to Reject' Means in a Hypothesis Test
- Definition of a Hypothesis
- Null Hypothesis Definition and Examples
- Scientific Method Vocabulary Terms
- Null Hypothesis and Alternative Hypothesis
- Hypothesis Test for the Difference of Two Population Proportions
- How to Conduct a Hypothesis Test
- What Is a P-Value?
- What Are the Elements of a Good Hypothesis?
- Hypothesis Test Example
- What Is the Difference Between Alpha and P-Values?
- Understanding Path Analysis
- An Example of a Hypothesis Test
Module 9: Hypothesis Testing With One Sample
Null and alternative hypotheses, learning outcomes.
- Describe hypothesis testing in general and in practice
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.
H a : The alternative hypothesis : It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make adecision. There are two options for a decision . They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.
Mathematical Symbols Used in H 0 and H a :
| equal (=) | not equal (≠) greater than (>) less than (<) |
| greater than or equal to (≥) | less than (<) |
| less than or equal to (≤) | more than (>) |
H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.
H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30
H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.
H 0 : The drug reduces cholesterol by 25%. p = 0.25
H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:
H 0 : μ = 2.0
H a : μ ≠ 2.0
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 66 H a : μ __ 66
- H 0 : μ = 66
- H a : μ ≠ 66
We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:
H 0 : μ ≥ 5
H a : μ < 5
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 45 H a : μ __ 45
- H 0 : μ ≥ 45
- H a : μ < 45
In an issue of U.S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.
H 0 : p ≤ 0.066
H a : p > 0.066
On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : p __ 0.40 H a : p __ 0.40
- H 0 : p = 0.40
- H a : p > 0.40
Concept Review
In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis , typically denoted with H 0 . The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality (=, ≤ or ≥) Always write the alternative hypothesis , typically denoted with H a or H 1 , using less than, greater than, or not equals symbols, i.e., (≠, >, or <). If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis. Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.
Formula Review
H 0 and H a are contradictory.
- OpenStax, Statistics, Null and Alternative Hypotheses. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:58/Introductory_Statistics . License : CC BY: Attribution
- Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
- Simple hypothesis testing | Probability and Statistics | Khan Academy. Authored by : Khan Academy. Located at : https://youtu.be/5D1gV37bKXY . License : All Rights Reserved . License Terms : Standard YouTube License
Have a thesis expert improve your writing
Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.
- Knowledge Base
- Null and Alternative Hypotheses | Definitions & Examples
Null and Alternative Hypotheses | Definitions & Examples
Published on 5 October 2022 by Shaun Turney . Revised on 6 December 2022.
The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :
- Null hypothesis (H 0 ): There’s no effect in the population .
- Alternative hypothesis (H A ): There’s an effect in the population.
The effect is usually the effect of the independent variable on the dependent variable .
Table of contents
Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, differences between null and alternative hypotheses, how to write null and alternative hypotheses, frequently asked questions about null and alternative hypotheses.
The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”, the null hypothesis (H 0 ) answers “No, there’s no effect in the population.” On the other hand, the alternative hypothesis (H A ) answers “Yes, there is an effect in the population.”
The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample.
You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.
The null hypothesis is the claim that there’s no effect in the population.
If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.
Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept. Be careful not to say you “prove” or “accept” the null hypothesis.
Null hypotheses often include phrases such as “no effect”, “no difference”, or “no relationship”. When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).
Examples of null hypotheses
The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.
| ( ) | ||
| Does tooth flossing affect the number of cavities? | Tooth flossing has on the number of cavities. | test: The mean number of cavities per person does not differ between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ = µ . |
| Does the amount of text highlighted in the textbook affect exam scores? | The amount of text highlighted in the textbook has on exam scores. | : There is no relationship between the amount of text highlighted and exam scores in the population; β = 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression.* | test: The proportion of people with depression in the daily-meditation group ( ) is greater than or equal to the no-meditation group ( ) in the population; ≥ . |
*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .
The alternative hypothesis (H A ) is the other answer to your research question . It claims that there’s an effect in the population.
Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.
The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.
Alternative hypotheses often include phrases such as “an effect”, “a difference”, or “a relationship”. When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes > or <). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.
Examples of alternative hypotheses
The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.
| Does tooth flossing affect the number of cavities? | Tooth flossing has an on the number of cavities. | test: The mean number of cavities per person differs between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ ≠ µ . |
| Does the amount of text highlighted in a textbook affect exam scores? | The amount of text highlighted in the textbook has an on exam scores. | : There is a relationship between the amount of text highlighted and exam scores in the population; β ≠ 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression. | test: The proportion of people with depression in the daily-meditation group ( ) is less than the no-meditation group ( ) in the population; < . |
Null and alternative hypotheses are similar in some ways:
- They’re both answers to the research question
- They both make claims about the population
- They’re both evaluated by statistical tests.
However, there are important differences between the two types of hypotheses, summarized in the following table.
| A claim that there is in the population. | A claim that there is in the population. | |
|
| ||
| Equality symbol (=, ≥, or ≤) | Inequality symbol (≠, <, or >) | |
| Rejected | Supported | |
| Failed to reject | Not supported |
To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.
The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:
Does independent variable affect dependent variable ?
- Null hypothesis (H 0 ): Independent variable does not affect dependent variable .
- Alternative hypothesis (H A ): Independent variable affects dependent variable .
Test-specific
Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.
| ( ) | ||
| test
with two groups | The mean dependent variable does not differ between group 1 (µ ) and group 2 (µ ) in the population; µ = µ . | The mean dependent variable differs between group 1 (µ ) and group 2 (µ ) in the population; µ ≠ µ . |
| with three groups | The mean dependent variable does not differ between group 1 (µ ), group 2 (µ ), and group 3 (µ ) in the population; µ = µ = µ . | The mean dependent variable of group 1 (µ ), group 2 (µ ), and group 3 (µ ) are not all equal in the population. |
| There is no correlation between independent variable and dependent variable in the population; ρ = 0. | There is a correlation between independent variable and dependent variable in the population; ρ ≠ 0. | |
| There is no relationship between independent variable and dependent variable in the population; β = 0. | There is a relationship between independent variable and dependent variable in the population; β ≠ 0. | |
| Two-proportions test | The dependent variable expressed as a proportion does not differ between group 1 ( ) and group 2 ( ) in the population; = . | The dependent variable expressed as a proportion differs between group 1 ( ) and group 2 ( ) in the population; ≠ . |
Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.
The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).
The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).
A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).
A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.
Turney, S. (2022, December 06). Null and Alternative Hypotheses | Definitions & Examples. Scribbr. Retrieved 2 July 2024, from https://www.scribbr.co.uk/stats/null-and-alternative-hypothesis/
Is this article helpful?

Shaun Turney
Other students also liked, levels of measurement: nominal, ordinal, interval, ratio, the standard normal distribution | calculator, examples & uses, types of variables in research | definitions & examples.
Talk to our experts
1800-120-456-456
- Null Hypothesis

Before understanding the Null Hypothesis in detail, let us first understand the definition of the Hypothesis.
In Statistics, a hypothesis can be defined as a formal statement, which gives an explanation about the relationship between any two or more variables of the specified population.
Hypothesis helps the researcher to translate any given problem to a clear explanation for the outcome of the study.
Hypothesis clearly explains and predicts the expected outcome and it indicates the types of experimental design and directs the study of any research process.
What Is The Null Hypothesis?
We can define a null hypothesis as a general statement or a default position that says there is no relationship between two measured phenomena or there is no association among groups.
Why is Null Hypothesis Important?
Testing (which involves accepting, approving, rejecting, or disproving) the null hypothesis and thus concluding that there are or we can say that there are no grounds for believing that there is any relationship between two phenomena is basically a central task in the modern practice of science; in the field of statistics.
To be more specific, hypothesis testing gives precise criteria for rejecting or accepting a null hypothesis within a level known as the confidence level.
Null Hypothesis Symbol-
A Null Hypothesis is denoted by the symbol H 0 in statistics. It is usually pronounced as “h-nought” or “H-null”. The Subscript in H is the digit 0.
Null Hypothesis Principle and When is A Null Hypothesis Rejected?
The principle followed for null hypothesis testing is basically collecting the data and determining the chances of a given set of data during the study on any given random sample, assuming that the null hypothesis is true.
Suppose, if the given data does not face the expected null hypothesis, then the outcome we will get will be quite weaker and they conclude that by saying that the given set of data does not provide strong evidence against the null hypothesis which is because of insufficient evidence.
Finally, this leads to null hypothesis rejection.
Null Hypothesis Formula or How Do You Find The Null Hypothesis :
So far, understanding the concept of null hypothesis, let’s now discuss the null hypothesis formula:
Here, the null hypothesis formula is given below.
H 0 : p = p 0
The formula for the alternative hypothesis can be written as: H a = p >p 0 , and < p 0 ≠ p 0
The formula for the test static is denoted by:
\[Z=\frac{P-P_{0}}{\sqrt{\frac{P-P_{0}}{n}}}\]
Remember that, p 0 here is the null hypothesis.
Types of Null Hypothesis.
There are 4 different types of Null hypothesis. Each of them is explained below with examples.
Simple Hypothesis: A simple Hypothesis is the one in which the relationship between two variables is predicted. One is an independent variable and the other is a dependent variable. A simple Hypothesis completely specifies the population distribution. An example of a simple Hypothesis is “Consuming sugar drinks daily leads to being overweight.”
Composite hypothesis. A Composite hypothesis describes the relationship between two or more independent variables and two or more dependent variables. In this hypothesis, the population distribution is not specified. An example of the Composite hypothesis is stated below. “ Individuals who consume sugar drinks daily and have a family history of health issues are more likely to become overweight and develop diabetes.”
Exact hypothesis. In this hypothesis, the exact value of the parameter or variable is defined. All the assumptions made during the derivation of the hypothesis are met in the exact hypothesis. An example of an exact hypothesis is, “ Students in a division score an average 17 out of 25 in exams. Hence, μ=17.”
Inexact hypothesis. Unlike the exact hypothesis, the exact value of the parameter or variable is not defined in the Inexact type of Hypothesis. Instead, a specific range or interval of the parameter is stated. For example, Students in class score an average between 12 to 15 out of 20 in exams. Hence, 12< μ< 15.
Null Hypothesis Problem Problem : A researcher thinks that if the knee surgery patients go to physical therapy twice a week (instead of going 3 times), their recovery period will be longer. Given average recovery time knee surgery patients are given 8.2 weeks.
Step 1: First, we need to figure out the hypothesis from the problem . The hypothesis is usually hidden in a word problem that you need to figure out. The hypothesis that has been given in the above question is “I expect the average recovery period to be greater than 8.2 weeks.”
Step 2: You need to convert the hypothesis to math . Remember that the average can be sometimes written as μ.
H 1 : μ > 8.2(average)
Step 3: Now state what will happen if the hypothesis doesn’t come true. If the recovery time is not greater than the given average that is 8.2 weeks, there are only two possibilities, that the recovery time is equal to 8.2 weeks or it is less than 8.2 weeks.
H 0 : μ ≤ 8.2
H 0 (The null hypothesis): μ (the average) ≤ (is less than or equal to) 8.2
H 0 🡪 μ 1 = μ 2 where
H 0 is the null hypothesis,
μ 1 is the mean of population 1, and
μ 2 is the mean of population 2.
A stronger null hypothesis denotes that if two samples are drawn from the same given population, such that the variances and shapes of the given distributions are also equal.
Examples of situations where hypothesis tests are used in the real world.
Is there a 100% chance of getting affected by dengue?
Answer : There could be chances of getting affected by dengue but the chances of getting affected by dengue are not 100%.
Do teenagers these days use mobile phones more than adults to access the internet?
Answer : Age has no limit and is not a factor that we can use mobile phones to access the internet.
Does having the fruit apple daily will not cause fever?
Answer : Having an apple daily does not assure of not having fever, but on the other hand it does increase the immunity to fight against such diseases.
Are children better at performing mathematical calculations than adults?
Answer : Again in this example too, age has no effect on Mathematical skills.
Hypothesis tests are often conducted in botany to determine whether some new treatment, fertilizer or chemical can cause increased growth, stamina or immunity in plants and animals.
Suppose, a botanist believes that a certain fertilizer will cause plants to grow more during a 1 month period than what they actually grow. Currently, they grow to 20 inches. To test the effectiveness of the fertilizer, the botanist applies the fertilizer to each of the plants in her lab for a month. Then performs a hypothesis test using the following hypothesis: H 0 : μ = 20 inches as the effect is nil on the mean plant growth by the fertilizer.
H A : μ > 20 inches (the fertilizer will cause mean plant growth to increase)
If the p-value of the test is significantly less then it will reject the null hypothesis and as a result, the fertilizer leads to increased plant growth.
In clinical trials, hypothesis tests are often used to determine whether some new treatment, drug, procedure, etc. cause improved outcomes in patients and thus elevate the treatment levels. Suppose a doctor wishes to test a new drug that reduces blood pressure in obese patients. To test its effectiveness, the doctor may measure the blood pressure of 40 patients before and after using the new drug for a month. Then a hypothesis test is performed using the following hypothesis. H 0 : μafter = μbefore means the mean blood pressure is the same before and after using the drug
H A : μafter < μbefore (the mean blood pressure is less after using the drug)
Hypothesis tests are often conducted in business organizations to determine whether a new advertising campaign will get more leads and cause an increase in sales. Suppose, the executive team of an organization believes that spending more on digital advertising leads to increased sales. To test this, the organization may increase money spent on digital advertising during a 3 month period and collect data to see if overall sales have increased or not. A hypothesis test can be performed using the following hypothesis.
H 0 : μafter = μbefore signifies the mean sales is the same before and after spending more on advertising
H A : μafter > μbefore (the mean sales increased spending more on advertising)
Apart from just the above 3 examples, hypothesis testing is widely used in research centers, chemical laboratories, stock market predictions, the Investment industry and several business organizations.
Decision errors.
There are two types of decision errors that can happen when doing a hypothesis test. They are described below.
Type I error: This happens when one rejects the null hypothesis despite the null hypothesis being true. The probability of making a type I error is equal to the alpha level significantly
Type II error. This happens when one fails to reject the null hypothesis when it is actually false. The probability of committing a type II error is the power of the test.
Importance of Hypothesis testing in real life and examples
The main aim of a hypothesis statement in statistics is to determine whether or not some hypothesis of a population parameter is true or false. It is an essential part of the procedures in statistics.
A hypothesis test evaluates two mutually exclusive statements and determines which statement is best supported by sample data. A discovery or a new finding holds a significant value when supported by a hypothesis test. Because the hypothesis test provides sufficient evidence to check the credibility of the given data.
To conduct a hypothesis test in the practical world, researchers obtain a random sample from the population and perform a hypothesis test on the sample data using Null and Alternative hypotheses.
Difference between Null Hypothesis and Alternative Hypothesis.
Parameter | Null Hypothesis | Alternative Hypothesis |
Observation | Concludes that the results are observed as a result of chance. | Concludes that the results are observed due to some real causes. |
Symbol | Denoted by H0 | Denoted by HA |
Definition | States that two factors or groups are unrelated and there is no difference between certain characteristics of a population. | States that there is a relation between the two variables or groups under consideration. |
Nature | Researchers usually try to disprove the null hypothesis. | Researchers try to prove an alternative hypothesis. |
Acceptance | If the obtained p-value is greater than the level of significance, then the null hypothesis is accepted. | If the obtained p-value is smaller than the level of significance, then an alternative hypothesis is accepted. |

FAQs on Null Hypothesis
1. Why is a null hypothesis important and can you accept a null hypothesis?
The purpose and the importance of the null hypothesis and alternative hypothesis are that they provide an approximate description of any given phenomena. The purpose of the null hypothesis is to provide the researcher or an investigator with the relational statement that is directly tested in any research study.
A null hypothesis is a hypothesis that is never acceptable. We either reject them or we fail to reject them. Hence, failing to reject the null hypothesis does not mean that we have shown that there is no difference in accepting the null hypothesis.
2. State one example where a Null hypothesis is applied in a practical life scenario?
The concept of null hypothesis has a variety of practical applications. Let us take the example of stock investment, buying shares of a company. The annual return of company stock when invested for a long duration is assumed to be 7.5%.
Now to test if the assumption is true or false, we consider the null hypothesis to be, ”the mean annual return for XYZ company shares is not 7.5%”. To test this hypothesis, we first accept the null hypothesis.
We then check the history of the stock performance of the last 5 years of XYZ company and then calculate the mean of the annual return. The result is then compared to the assumed annual return of 7.5%.
If it turns out that the average annual return of the last 5 years is 7.5%, then the null hypothesis is rejected. And the alternative hypothesis is accepted.
3. What is the purpose of Hypothesis testing?
Hypothesis testing is a statistical process of testing an assumption regarding a particular phenomenon or parameter. Often a good theory can make accurate predictions. However, for an analyst, hypothesis testing is a rigorous way of backing up his prediction with statistical analysis to support the predictions. It is also helpful to determine sufficient statistical evidence that can favor a certain hypothesis about the specified parameter.
In simple words, hypothesis testing is a systematic approach to assessing theories through observations and then determining whether the stated statement is true or false.
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
AP®︎/College Statistics
Course: ap®︎/college statistics > unit 10.
- Idea behind hypothesis testing
- Examples of null and alternative hypotheses
Writing null and alternative hypotheses
- P-values and significance tests
- Comparing P-values to different significance levels
- Estimating a P-value from a simulation
- Estimating P-values from simulations
- Using P-values to make conclusions
- (Choice A) H 0 : p = 0.1 H a : p ≠ 0.1 A H 0 : p = 0.1 H a : p ≠ 0.1
- (Choice B) H 0 : p ≠ 0.1 H a : p = 0.1 B H 0 : p ≠ 0.1 H a : p = 0.1
- (Choice C) H 0 : p = 0.1 H a : p > 0.1 C H 0 : p = 0.1 H a : p > 0.1
- (Choice D) H 0 : p = 0.1 H a : p < 0.1 D H 0 : p = 0.1 H a : p < 0.1
- Thesis Action Plan New
- Academic Project Planner
Literature Navigator
Thesis dialogue blueprint, writing wizard's template, research proposal compass.
- Why students love us
- Why professors love us
- Rebels Blog (Free)
- Why we are different
- All Products
- Coming Soon
Formulating a Null Hypothesis: Key Elements to Consider

The concept of the null hypothesis is a cornerstone of statistical hypothesis testing. In the article 'Formulating a Null Hypothesis: Key Elements to Consider,' we delve into what a null hypothesis is, why it's crucial for research, and how to properly formulate one. This article offers a comprehensive guide for researchers and students alike, providing the necessary tools to craft a null hypothesis that effectively sets the stage for rigorous scientific inquiry.
Key Takeaways
- A null hypothesis (H0) is a statement that there is no effect or no difference, and it serves as the starting point for statistical testing.
- Formulating a null hypothesis involves defining a clear and concise research question, stating the hypothesis in a way that allows for empirical testing, and considering the potential for Type I errors.
- Evaluating a null hypothesis requires understanding its role in research design, recognizing common misconceptions, and being aware of the challenges in crafting a hypothesis that is both testable and meaningful.
Understanding the Null Hypothesis
Defining the null hypothesis.
The null hypothesis , often represented as H0, is the default assumption that there is no effect or no difference in the context of scientific research. It posits a position of neutrality, suggesting that any observed variations in data are due to chance rather than a specific cause or intervention. Formulating a null hypothesis is a foundational step in hypothesis testing , where it is contrasted with an alternative hypothesis (Ha) that predicts an effect or difference.
Importance of the Null Hypothesis in Research
In the research process, the null hypothesis plays a critical role as it provides a benchmark against which the validity of the study's findings is assessed. It is essential for identifying variables, crafting clear hypotheses, and conducting targeted research that advances scientific knowledge. The research process involves revisiting initial assumptions , evaluating the design, considering alternative explanations, adjusting methodology, and addressing limitations when faced with contradictory data.

Common Misconceptions and Clarifications
There are several misconceptions about the null hypothesis that can lead to confusion. One common error is the belief that a failure to reject the null hypothesis is evidence of no effect, which is not necessarily true. It may simply indicate insufficient evidence to support the alternative hypothesis. Another misunderstanding is equating the null hypothesis with the belief that there is no relationship between variables, which overlooks the fact that it is a tool for statistical testing, not a definitive statement about reality.
Crafting the Null Hypothesis
Steps for formulating a null hypothesis.
When you're learning how to write a thesis or a research paper, formulating a null hypothesis is a critical step. Begin by clearly defining the variables or groups you are studying. Next, state the null hypothesis as a position of no effect or no difference, implying that any observed effect is due to chance. Ensure that your hypothesis is testable and measurable, and consider any potential limitations or biases that could affect the results.
Examples of Null Hypotheses in Various Disciplines
In various academic fields, the null hypothesis takes on different forms. For instance, in psychology, a null hypothesis might state that a new therapy has no effect on depression levels compared to the standard treatment. In ecology, it could assert that there is no significant difference in biodiversity between two protected areas. These examples illustrate how the null hypothesis is tailored to the specific research question and discipline.
Evaluating the Null Hypothesis: Considerations and Challenges
Evaluating the null hypothesis involves selecting appropriate statistical tests and determining the significance level. It's essential to understand the difference between statistical and practical significance . Writing anxiety can arise during this phase, especially when interpreting complex data. However, a systematic approach to hypothesis testing can help alleviate this stress and lead to meaningful research conclusions.
Embarking on the journey of thesis writing can be daunting, but with Research Rebels , you're not alone. Our step-by-step Thesis Action Plan is designed to transform your anxiety and uncertainty into confidence and clarity. From crafting the perfect Null Hypothesis to navigating complex research methodologies, we've got you covered. Don't let sleepless nights hinder your academic success. Visit our website now to claim your special offer and take the first step towards a stress-free thesis experience.
In conclusion, formulating a null hypothesis is a fundamental step in the research process, serving as a critical benchmark against which scientific evidence is measured. A well-constructed null hypothesis provides clarity and direction, allowing for rigorous testing and meaningful interpretation of results. It is essential to articulate the null hypothesis with precision, ensuring it is testable, falsifiable, and appropriately framed to reflect the absence of an effect or relationship. By carefully considering the key elements discussed in this article, researchers can establish a robust foundation for their empirical inquiries, ultimately contributing to the advancement of knowledge within their respective fields.
Frequently Asked Questions
What is the null hypothesis in research.
The null hypothesis (H0) is a statement in research that suggests there is no significant effect or difference between certain populations, conditions, or variables. It is the default assumption that there is no relationship or impact, and it is tested to determine if there is evidence to support an alternative hypothesis.
How do you formulate a null hypothesis?
To formulate a null hypothesis, first identify the research question or problem. Then, state the null hypothesis in a way that it asserts no effect or no difference between groups or variables. It should be clear, specific, and testable, often structured as H0: parameter = value (e.g., H0: μ1 = μ2).
What are common challenges in evaluating the null hypothesis?
Challenges in evaluating the null hypothesis include ensuring the study design and data collection methods are appropriate, selecting the correct statistical test, interpreting the results correctly, and understanding the potential for Type I (false positive) and Type II (false negative) errors.

Writing a Thesis When You Don't Have Much Time: Effective Strategies
How to deal with thesis burnout: tips for staying motivated, how to deal with a total lack of motivation, stress, and anxiety when finishing my master's thesis, how do i start writing my thesis: a beginner's guide, how to write a thesis: a step-by-step guide with tips.

Demystifying Research: Understanding the Difference Between a Problem and a Hypothesis

Avoiding Procrastination Pitfalls: Bachelor Thesis Progress and Weekend Celebrations

How Do You Write a Hypothesis for a Research Paper? Step-by-Step Guide

How to Write a Thesis Fast: Tips and Strategies for Success

The Note-Taking Debate: Pros and Cons of Digital and Analog Methods

Thesis Action Plan

- Rebels Blog
- Blog Articles
- Terms and Conditions
- Payment and Shipping Terms
- Privacy Policy
- Return Policy
© 2024 Research Rebels, All rights reserved.
Your cart is currently empty.
- PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
- EDIT Edit this Article
- EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
- Browse Articles
- Learn Something New
- Quizzes Hot
- This Or That Game
- Train Your Brain
- Explore More
- Support wikiHow
- About wikiHow
- Log in / Sign up
- Education and Communications
- College University and Postgraduate
- Academic Writing
Writing Null Hypotheses in Research and Statistics
Last Updated: January 17, 2024 Fact Checked
This article was co-authored by Joseph Quinones and by wikiHow staff writer, Jennifer Mueller, JD . Joseph Quinones is a High School Physics Teacher working at South Bronx Community Charter High School. Joseph specializes in astronomy and astrophysics and is interested in science education and science outreach, currently practicing ways to make physics accessible to more students with the goal of bringing more students of color into the STEM fields. He has experience working on Astrophysics research projects at the Museum of Natural History (AMNH). Joseph recieved his Bachelor's degree in Physics from Lehman College and his Masters in Physics Education from City College of New York (CCNY). He is also a member of a network called New York City Men Teach. There are 7 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 27,020 times.
Are you working on a research project and struggling with how to write a null hypothesis? Well, you've come to the right place! Start by recognizing that the basic definition of "null" is "none" or "zero"—that's your biggest clue as to what a null hypothesis should say. Keep reading to learn everything you need to know about the null hypothesis, including how it relates to your research question and your alternative hypothesis as well as how to use it in different types of studies.
Things You Should Know
- Write a research null hypothesis as a statement that the studied variables have no relationship to each other, or that there's no difference between 2 groups.

- Adjust the format of your null hypothesis to match the statistical method you used to test it, such as using "mean" if you're comparing the mean between 2 groups.
What is a null hypothesis?

- Research hypothesis: States in plain language that there's no relationship between the 2 variables or there's no difference between the 2 groups being studied.
- Statistical hypothesis: States the predicted outcome of statistical analysis through a mathematical equation related to the statistical method you're using.
Examples of Null Hypotheses

Null Hypothesis vs. Alternative Hypothesis

- For example, your alternative hypothesis could state a positive correlation between 2 variables while your null hypothesis states there's no relationship. If there's a negative correlation, then both hypotheses are false.

- You need additional data or evidence to show that your alternative hypothesis is correct—proving the null hypothesis false is just the first step.
- In smaller studies, sometimes it's enough to show that there's some relationship and your hypothesis could be correct—you can leave the additional proof as an open question for other researchers to tackle.
How do I test a null hypothesis?

- Group means: Compare the mean of the variable in your sample with the mean of the variable in the general population. [6] X Research source
- Group proportions: Compare the proportion of the variable in your sample with the proportion of the variable in the general population. [7] X Research source
- Correlation: Correlation analysis looks at the relationship between 2 variables—specifically, whether they tend to happen together. [8] X Research source
- Regression: Regression analysis reveals the correlation between 2 variables while also controlling for the effect of other, interrelated variables. [9] X Research source
Templates for Null Hypotheses

- Research null hypothesis: There is no difference in the mean [dependent variable] between [group 1] and [group 2].

- Research null hypothesis: The proportion of [dependent variable] in [group 1] and [group 2] is the same.

- Research null hypothesis: There is no correlation between [independent variable] and [dependent variable] in the population.

- Research null hypothesis: There is no relationship between [independent variable] and [dependent variable] in the population.

Expert Q&A

You Might Also Like

Expert Interview

Thanks for reading our article! If you’d like to learn more about physics, check out our in-depth interview with Joseph Quinones .
- ↑ https://online.stat.psu.edu/stat100/lesson/10/10.1
- ↑ https://online.stat.psu.edu/stat501/lesson/2/2.12
- ↑ https://support.minitab.com/en-us/minitab/21/help-and-how-to/statistics/basic-statistics/supporting-topics/basics/null-and-alternative-hypotheses/
- ↑ https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5635437/
- ↑ https://online.stat.psu.edu/statprogram/reviews/statistical-concepts/hypothesis-testing
- ↑ https://education.arcus.chop.edu/null-hypothesis-testing/
- ↑ https://sphweb.bumc.bu.edu/otlt/mph-modules/bs/bs704_hypothesistest-means-proportions/bs704_hypothesistest-means-proportions_print.html
About This Article

- Send fan mail to authors
Reader Success Stories
Dec 3, 2022
Did this article help you?
Featured Articles

Trending Articles

Watch Articles

- Terms of Use
- Privacy Policy
- Do Not Sell or Share My Info
- Not Selling Info
Get all the best how-tos!
Sign up for wikiHow's weekly email newsletter
- Math Article
Null Hypothesis

In mathematics, Statistics deals with the study of research and surveys on the numerical data. For taking surveys, we have to define the hypothesis. Generally, there are two types of hypothesis. One is a null hypothesis, and another is an alternative hypothesis .
In probability and statistics, the null hypothesis is a comprehensive statement or default status that there is zero happening or nothing happening. For example, there is no connection among groups or no association between two measured events. It is generally assumed here that the hypothesis is true until any other proof has been brought into the light to deny the hypothesis. Let us learn more here with definition, symbol, principle, types and example, in this article.
Table of contents:
- Comparison with Alternative Hypothesis
Null Hypothesis Definition
The null hypothesis is a kind of hypothesis which explains the population parameter whose purpose is to test the validity of the given experimental data. This hypothesis is either rejected or not rejected based on the viability of the given population or sample . In other words, the null hypothesis is a hypothesis in which the sample observations results from the chance. It is said to be a statement in which the surveyors wants to examine the data. It is denoted by H 0 .
Null Hypothesis Symbol
In statistics, the null hypothesis is usually denoted by letter H with subscript ‘0’ (zero), such that H 0 . It is pronounced as H-null or H-zero or H-nought. At the same time, the alternative hypothesis expresses the observations determined by the non-random cause. It is represented by H 1 or H a .
Null Hypothesis Principle
The principle followed for null hypothesis testing is, collecting the data and determining the chances of a given set of data during the study on some random sample, assuming that the null hypothesis is true. In case if the given data does not face the expected null hypothesis, then the outcome will be quite weaker, and they conclude by saying that the given set of data does not provide strong evidence against the null hypothesis because of insufficient evidence. Finally, the researchers tend to reject that.
Null Hypothesis Formula
Here, the hypothesis test formulas are given below for reference.
The formula for the null hypothesis is:
H 0 : p = p 0
The formula for the alternative hypothesis is:
H a = p >p 0 , < p 0 ≠ p 0
The formula for the test static is:
Remember that, p 0 is the null hypothesis and p – hat is the sample proportion.
Also, read:
Types of Null Hypothesis
There are different types of hypothesis. They are:
Simple Hypothesis
It completely specifies the population distribution. In this method, the sampling distribution is the function of the sample size.
Composite Hypothesis
The composite hypothesis is one that does not completely specify the population distribution.
Exact Hypothesis
Exact hypothesis defines the exact value of the parameter. For example μ= 50
Inexact Hypothesis
This type of hypothesis does not define the exact value of the parameter. But it denotes a specific range or interval. For example 45< μ <60
Null Hypothesis Rejection
Sometimes the null hypothesis is rejected too. If this hypothesis is rejected means, that research could be invalid. Many researchers will neglect this hypothesis as it is merely opposite to the alternate hypothesis. It is a better practice to create a hypothesis and test it. The goal of researchers is not to reject the hypothesis. But it is evident that a perfect statistical model is always associated with the failure to reject the null hypothesis.
How do you Find the Null Hypothesis?
The null hypothesis says there is no correlation between the measured event (the dependent variable) and the independent variable. We don’t have to believe that the null hypothesis is true to test it. On the contrast, you will possibly assume that there is a connection between a set of variables ( dependent and independent).
When is Null Hypothesis Rejected?
The null hypothesis is rejected using the P-value approach. If the P-value is less than or equal to the α, there should be a rejection of the null hypothesis in favour of the alternate hypothesis. In case, if P-value is greater than α, the null hypothesis is not rejected.
Null Hypothesis and Alternative Hypothesis
Now, let us discuss the difference between the null hypothesis and the alternative hypothesis.
|
|
| |
| 1 | The null hypothesis is a statement. There exists no relation between two variables | Alternative hypothesis a statement, there exists some relationship between two measured phenomenon |
| 2 | Denoted by H | Denoted by H |
| 3 | The observations of this hypothesis are the result of chance | The observations of this hypothesis are the result of real effect |
| 4 | The mathematical formulation of the null hypothesis is an equal sign | The mathematical formulation alternative hypothesis is an inequality sign such as greater than, less than, etc. |
Null Hypothesis Examples
Here, some of the examples of the null hypothesis are given below. Go through the below ones to understand the concept of the null hypothesis in a better way.
If a medicine reduces the risk of cardiac stroke, then the null hypothesis should be “the medicine does not reduce the chance of cardiac stroke”. This testing can be performed by the administration of a drug to a certain group of people in a controlled way. If the survey shows that there is a significant change in the people, then the hypothesis is rejected.
Few more examples are:
1). Are there is 100% chance of getting affected by dengue?
Ans: There could be chances of getting affected by dengue but not 100%.
2). Do teenagers are using mobile phones more than grown-ups to access the internet?
Ans: Age has no limit on using mobile phones to access the internet.
3). Does having apple daily will not cause fever?
Ans: Having apple daily does not assure of not having fever, but increases the immunity to fight against such diseases.
4). Do the children more good in doing mathematical calculations than grown-ups?
Ans: Age has no effect on Mathematical skills.
In many common applications, the choice of the null hypothesis is not automated, but the testing and calculations may be automated. Also, the choice of the null hypothesis is completely based on previous experiences and inconsistent advice. The choice can be more complicated and based on the variety of applications and the diversity of the objectives.
The main limitation for the choice of the null hypothesis is that the hypothesis suggested by the data is based on the reasoning which proves nothing. It means that if some hypothesis provides a summary of the data set, then there would be no value in the testing of the hypothesis on the particular set of data.
Frequently Asked Questions on Null Hypothesis
What is meant by the null hypothesis.
In Statistics, a null hypothesis is a type of hypothesis which explains the population parameter whose purpose is to test the validity of the given experimental data.
What are the benefits of hypothesis testing?
Hypothesis testing is defined as a form of inferential statistics, which allows making conclusions from the entire population based on the sample representative.
When a null hypothesis is accepted and rejected?
The null hypothesis is either accepted or rejected in terms of the given data. If P-value is less than α, then the null hypothesis is rejected in favor of the alternative hypothesis, and if the P-value is greater than α, then the null hypothesis is accepted in favor of the alternative hypothesis.
Why is the null hypothesis important?
The importance of the null hypothesis is that it provides an approximate description of the phenomena of the given data. It allows the investigators to directly test the relational statement in a research study.
How to accept or reject the null hypothesis in the chi-square test?
If the result of the chi-square test is bigger than the critical value in the table, then the data does not fit the model, which represents the rejection of the null hypothesis.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz
Visit BYJU’S for all Maths related queries and study materials
Your result is as below
Request OTP on Voice Call
| MATHS Related Links | |
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
Methodology
- How to Write a Strong Hypothesis | Steps & Examples
How to Write a Strong Hypothesis | Steps & Examples
Published on May 6, 2022 by Shona McCombes . Revised on November 20, 2023.
A hypothesis is a statement that can be tested by scientific research. If you want to test a relationship between two or more variables, you need to write hypotheses before you start your experiment or data collection .
Example: Hypothesis
Daily apple consumption leads to fewer doctor’s visits.
Table of contents
What is a hypothesis, developing a hypothesis (with example), hypothesis examples, other interesting articles, frequently asked questions about writing hypotheses.
A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.
A hypothesis is not just a guess – it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).
Variables in hypotheses
Hypotheses propose a relationship between two or more types of variables .
- An independent variable is something the researcher changes or controls.
- A dependent variable is something the researcher observes and measures.
If there are any control variables , extraneous variables , or confounding variables , be sure to jot those down as you go to minimize the chances that research bias will affect your results.
In this example, the independent variable is exposure to the sun – the assumed cause . The dependent variable is the level of happiness – the assumed effect .
Receive feedback on language, structure, and formatting
Professional editors proofread and edit your paper by focusing on:
- Academic style
- Vague sentences
- Style consistency
See an example

Step 1. Ask a question
Writing a hypothesis begins with a research question that you want to answer. The question should be focused, specific, and researchable within the constraints of your project.
Step 2. Do some preliminary research
Your initial answer to the question should be based on what is already known about the topic. Look for theories and previous studies to help you form educated assumptions about what your research will find.
At this stage, you might construct a conceptual framework to ensure that you’re embarking on a relevant topic . This can also help you identify which variables you will study and what you think the relationships are between them. Sometimes, you’ll have to operationalize more complex constructs.
Step 3. Formulate your hypothesis
Now you should have some idea of what you expect to find. Write your initial answer to the question in a clear, concise sentence.
4. Refine your hypothesis
You need to make sure your hypothesis is specific and testable. There are various ways of phrasing a hypothesis, but all the terms you use should have clear definitions, and the hypothesis should contain:
- The relevant variables
- The specific group being studied
- The predicted outcome of the experiment or analysis
5. Phrase your hypothesis in three ways
To identify the variables, you can write a simple prediction in if…then form. The first part of the sentence states the independent variable and the second part states the dependent variable.
In academic research, hypotheses are more commonly phrased in terms of correlations or effects, where you directly state the predicted relationship between variables.
If you are comparing two groups, the hypothesis can state what difference you expect to find between them.
6. Write a null hypothesis
If your research involves statistical hypothesis testing , you will also have to write a null hypothesis . The null hypothesis is the default position that there is no association between the variables. The null hypothesis is written as H 0 , while the alternative hypothesis is H 1 or H a .
- H 0 : The number of lectures attended by first-year students has no effect on their final exam scores.
- H 1 : The number of lectures attended by first-year students has a positive effect on their final exam scores.
| Research question | Hypothesis | Null hypothesis |
|---|---|---|
| What are the health benefits of eating an apple a day? | Increasing apple consumption in over-60s will result in decreasing frequency of doctor’s visits. | Increasing apple consumption in over-60s will have no effect on frequency of doctor’s visits. |
| Which airlines have the most delays? | Low-cost airlines are more likely to have delays than premium airlines. | Low-cost and premium airlines are equally likely to have delays. |
| Can flexible work arrangements improve job satisfaction? | Employees who have flexible working hours will report greater job satisfaction than employees who work fixed hours. | There is no relationship between working hour flexibility and job satisfaction. |
| How effective is high school sex education at reducing teen pregnancies? | Teenagers who received sex education lessons throughout high school will have lower rates of unplanned pregnancy teenagers who did not receive any sex education. | High school sex education has no effect on teen pregnancy rates. |
| What effect does daily use of social media have on the attention span of under-16s? | There is a negative between time spent on social media and attention span in under-16s. | There is no relationship between social media use and attention span in under-16s. |
If you want to know more about the research process , methodology , research bias , or statistics , make sure to check out some of our other articles with explanations and examples.
- Sampling methods
- Simple random sampling
- Stratified sampling
- Cluster sampling
- Likert scales
- Reproducibility
Statistics
- Null hypothesis
- Statistical power
- Probability distribution
- Effect size
- Poisson distribution
Research bias
- Optimism bias
- Cognitive bias
- Implicit bias
- Hawthorne effect
- Anchoring bias
- Explicit bias
Here's why students love Scribbr's proofreading services
Discover proofreading & editing
A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).
Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
McCombes, S. (2023, November 20). How to Write a Strong Hypothesis | Steps & Examples. Scribbr. Retrieved July 2, 2024, from https://www.scribbr.com/methodology/hypothesis/
Is this article helpful?
Shona McCombes
Other students also liked, construct validity | definition, types, & examples, what is a conceptual framework | tips & examples, operationalization | a guide with examples, pros & cons, "i thought ai proofreading was useless but..".
I've been using Scribbr for years now and I know it's a service that won't disappoint. It does a good job spotting mistakes”

Two-Tailed Hypothesis Tests: 3 Example Problems
In statistics, we use hypothesis tests to determine whether some claim about a population parameter is true or not.
Whenever we perform a hypothesis test, we always write a null hypothesis and an alternative hypothesis, which take the following forms:
H 0 (Null Hypothesis): Population parameter = ≤, ≥ some value
H A (Alternative Hypothesis): Population parameter <, >, ≠ some value
There are two types of hypothesis tests:
- One-tailed test : Alternative hypothesis contains either < or > sign
- Two-tailed test : Alternative hypothesis contains the ≠ sign
In a two-tailed test , the alternative hypothesis always contains the not equal ( ≠ ) sign.
This indicates that we’re testing whether or not some effect exists, regardless of whether it’s a positive or negative effect.
Check out the following example problems to gain a better understanding of two-tailed tests.
Example 1: Factory Widgets
Suppose it’s assumed that the average weight of a certain widget produced at a factory is 20 grams. However, one engineer believes that a new method produces widgets that weigh less than 20 grams.
To test this, he can perform a one-tailed hypothesis test with the following null and alternative hypotheses:
- H 0 (Null Hypothesis): μ = 20 grams
- H A (Alternative Hypothesis): μ ≠ 20 grams
This is an example of a two-tailed hypothesis test because the alternative hypothesis contains the not equal “≠” sign. The engineer believes that the new method will influence widget weight, but doesn’t specify whether it will cause average weight to increase or decrease.
To test this, he uses the new method to produce 20 widgets and obtains the following information:
- n = 20 widgets
- x = 19.8 grams
- s = 3.1 grams
Plugging these values into the One Sample t-test Calculator , we obtain the following results:
- t-test statistic: -0.288525
- two-tailed p-value: 0.776
Since the p-value is not less than .05, the engineer fails to reject the null hypothesis.
He does not have sufficient evidence to say that the true mean weight of widgets produced by the new method is different than 20 grams.
Example 2: Plant Growth
Suppose a standard fertilizer has been shown to cause a species of plants to grow by an average of 10 inches. However, one botanist believes a new fertilizer causes this species of plants to grow by an average amount different than 10 inches.
To test this, she can perform a one-tailed hypothesis test with the following null and alternative hypotheses:
- H 0 (Null Hypothesis): μ = 10 inches
- H A (Alternative Hypothesis): μ ≠ 10 inches
This is an example of a two-tailed hypothesis test because the alternative hypothesis contains the not equal “≠” sign. The botanist believes that the new fertilizer will influence plant growth, but doesn’t specify whether it will cause average growth to increase or decrease.
To test this claim, she applies the new fertilizer to a simple random sample of 15 plants and obtains the following information:
- n = 15 plants
- x = 11.4 inches
- s = 2.5 inches
- t-test statistic: 2.1689
- two-tailed p-value: 0.0478
Since the p-value is less than .05, the botanist rejects the null hypothesis.
She has sufficient evidence to conclude that the new fertilizer causes an average growth that is different than 10 inches.
Example 3: Studying Method
A professor believes that a certain studying technique will influence the mean score that her students receive on a certain exam, but she’s unsure if it will increase or decrease the mean score, which is currently 82.
To test this, she lets each student use the studying technique for one month leading up to the exam and then administers the same exam to each of the students.
She then performs a hypothesis test using the following hypotheses:
- H 0 : μ = 82
- H A : μ ≠ 82
This is an example of a two-tailed hypothesis test because the alternative hypothesis contains the not equal “≠” sign. The professor believes that the studying technique will influence the mean exam score, but doesn’t specify whether it will cause the mean score to increase or decrease.
To test this claim, the professor has 25 students use the new studying method and then take the exam. He collects the following data on the exam scores for this sample of students:
- t-test statistic: 3.6586
- two-tailed p-value: 0.0012
Since the p-value is less than .05, the professor rejects the null hypothesis.
She has sufficient evidence to conclude that the new studying method produces exam scores with an average score that is different than 82.
Additional Resources
The following tutorials provide additional information about hypothesis testing:
Introduction to Hypothesis Testing What is a Directional Hypothesis? When Do You Reject the Null Hypothesis?
Featured Posts
Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.
One Reply to “Two-Tailed Hypothesis Tests: 3 Example Problems”
i owe u my first born child
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Join the Statology Community
Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!
By subscribing you accept Statology's Privacy Policy.

IMAGES
VIDEO
COMMENTS
Step 1: Figure out the hypothesis from the problem. The hypothesis is usually hidden in a word problem, and is sometimes a statement of what you expect to happen in the experiment. The hypothesis in the above question is "I expect the average recovery period to be greater than 8.2 weeks.". Step 2: Convert the hypothesis to math.
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0, the —null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
Null Hypothesis Examples. "Hyperactivity is unrelated to eating sugar " is an example of a null hypothesis. If the hypothesis is tested and found to be false, using statistics, then a connection between hyperactivity and sugar ingestion may be indicated. A significance test is the most common statistical test used to establish confidence in a ...
Review. In a hypothesis test, sample data is evaluated in order to arrive at a decision about some type of claim.If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis, typically denoted with \(H_{0}\).The null is not rejected unless the hypothesis test shows otherwise.
Null hypothesis (H 0): Independent variable does not affect dependent variable. Alternative hypothesis (H a): Independent variable affects dependent variable. Test-specific template sentences. Once you know the statistical test you'll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose ...
Step 2: State the Alternate Hypothesis. The claim is that the students have above average IQ scores, so: H 1: μ > 100. The fact that we are looking for scores "greater than" a certain point means that this is a one-tailed test. Step 3: Draw a picture to help you visualize the problem. Step 4: State the alpha level.
H 0 (Null Hypothesis): Population parameter =, ≤, ≥ some value. H A (Alternative Hypothesis): Population parameter <, >, ≠ some value. Note that the null hypothesis always contains the equal sign. We interpret the hypotheses as follows: Null hypothesis: The sample data provides no evidence to support some claim being made by an individual.
It is the opposite of your research hypothesis. The alternative hypothesis--that is, the research hypothesis--is the idea, phenomenon, observation that you want to prove. If you suspect that girls take longer to get ready for school than boys, then: Alternative: girls time > boys time. Null: girls time <= boys time.
Null Hypothesis H 0: The correlation in the population is zero: ρ = 0. Alternative Hypothesis H A: The correlation in the population is not zero: ρ ≠ 0. For all these cases, the analysts define the hypotheses before the study. After collecting the data, they perform a hypothesis test to determine whether they can reject the null hypothesis.
To distinguish it from other hypotheses, the null hypothesis is written as H 0 (which is read as "H-nought," "H-null," or "H-zero"). A significance test is used to determine the likelihood that the results supporting the null hypothesis are not due to chance. A confidence level of 95% or 99% is common. Keep in mind, even if the confidence level is high, there is still a small chance the ...
Concept Review. In a hypothesis test, sample data is evaluated in order to arrive at a decision about some type of claim.If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis, typically denoted with H 0.The null is not rejected unless the hypothesis test shows otherwise.
The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test: Null hypothesis (H0): There's no effect in the population. Alternative hypothesis (HA): There's an effect in the population. The effect is usually the effect of the independent variable on the dependent ...
This statistics video tutorial provides a basic introduction into hypothesis testing. It provides examples and practice problems that explains how to state ...
Null Hypothesis Formula or How Do You Find The Null Hypothesis : So far, understanding the concept of null hypothesis, let's now discuss the null hypothesis formula: ... The hypothesis is usually hidden in a word problem that you need to figure out. The hypothesis that has been given in the above question is "I expect the average recovery ...
Present the findings in your results and discussion section. Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps. Table of contents. Step 1: State your null and alternate hypothesis. Step 2: Collect data. Step 3: Perform a statistical test.
The null hypothesis is a default hypothesis that a quantity to be measured is zero (null). Typically, the quantity to be measured is the difference between two situations. For instance, trying to determine if there is a positive proof that an effect has occurred or that samples derive from different batches. [7] [8]
Writing null and alternative hypotheses. A ketchup company regularly receives large shipments of tomatoes. For each shipment that is received, a supervisor takes a random sample of 500 tomatoes to see what percent of the sample is bruised and performs a significance test. If the sample shows convincing evidence that more than 10 % of the entire ...
A null hypothesis (H0) is a statement that there is no effect or no difference, and it serves as the starting point for statistical testing. Formulating a null hypothesis involves defining a clear and concise research question, stating the hypothesis in a way that allows for empirical testing, and considering the potential for Type I errors.
Write a statistical null hypothesis as a mathematical equation, such as. μ 1 = μ 2 {\displaystyle \mu _ {1}=\mu _ {2}} if you're comparing group means. Adjust the format of your null hypothesis to match the statistical method you used to test it, such as using "mean" if you're comparing the mean between 2 groups.
Here, the hypothesis test formulas are given below for reference. The formula for the null hypothesis is: H 0 : p = p 0. The formula for the alternative hypothesis is: H a = p >p 0, < p 0 ≠ p 0. The formula for the test static is: Remember that, p 0 is the null hypothesis and p - hat is the sample proportion.
The general procedure for testing the null hypothesis is as follows: State the null and alternative hypotheses. Specify α and the sample size. Select an appropriate statistical test. Collect data (note that the previous steps should be done before collecting data) Compute the test statistic based on the sample data.
Developing a hypothesis (with example) Step 1. Ask a question. Writing a hypothesis begins with a research question that you want to answer. The question should be focused, specific, and researchable within the constraints of your project. Example: Research question.
HA (Alternative Hypothesis): μ ≠ 10 inches. This is an example of a two-tailed hypothesis test because the alternative hypothesis contains the not equal "≠" sign. The botanist believes that the new fertilizer will influence plant growth, but doesn't specify whether it will cause average growth to increase or decrease.