Operations Research - Definition and formulation of Assignment Problem | 12th Business Maths and Statistics : Chapter 10 : Operations Research
Chapter: 12th business maths and statistics : chapter 10 : operations research, definition and formulation of assignment problem.
Definition and formulation
Consider the problem of assigning n jobs to n machines (one job to one machine). Let C ij be the cost of assigning i th job to the j th machine and x ij represents the assignment of i th job to the j th machine.
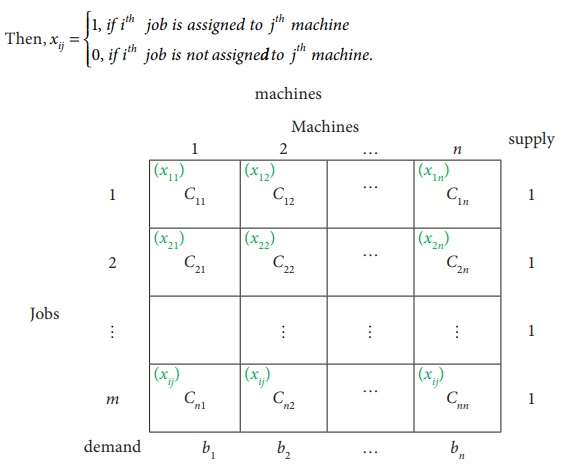
x ij is missing in any cell means that no assignment is made between the pair of job and machine.( i.e ) x ij = 0.
x ij presents in any cell means that an assignment is made their.In such cases x ij = 1
The assignment model can be written in LPP as follows
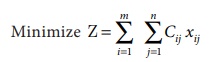
Subject to the constrains
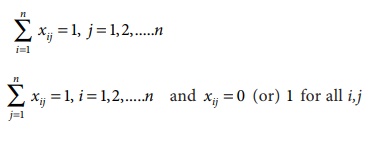
The optimum assignment schedule remains unaltered if we add or subtract a constant from all the elements of the row or column of the assignment cost matrix.
If for an assignment problem all C ij > 0 then an assignment schedule (x ij ) which satisfies ∑ C ij x ij = 0 must be optimal.
Related Topics
Privacy Policy , Terms and Conditions , DMCA Policy and Compliant
Copyright © 2018-2023 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.

Assignment Problem: Meaning, Methods and Variations | Operations Research
After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.
Meaning of Assignment Problem:
An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.
The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.
Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.
Definition of Assignment Problem:
ADVERTISEMENTS:
Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.
The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:
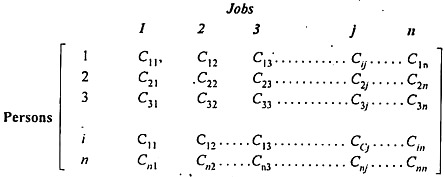
www.springer.com The European Mathematical Society
- StatProb Collection
- Recent changes
- Current events
- Random page
- Project talk
- Request account
- What links here
- Related changes
- Special pages
- Printable version
- Permanent link
- Page information
- View source
Assignment problem
The problem of optimally assigning $ m $ individuals to $ m $ jobs. It can be formulated as a linear programming problem that is a special case of the transport problem :
maximize $ \sum _ {i,j } c _ {ij } x _ {ij } $
$$ \sum _ { j } x _ {ij } = a _ {i} , i = 1 \dots m $$
(origins or supply),
$$ \sum _ { i } x _ {ij } = b _ {j} , j = 1 \dots n $$
(destinations or demand), where $ x _ {ij } \geq 0 $ and $ \sum a _ {i} = \sum b _ {j} $, which is called the balance condition. The assignment problem arises when $ m = n $ and all $ a _ {i} $ and $ b _ {j} $ are $ 1 $.
If all $ a _ {i} $ and $ b _ {j} $ in the transposed problem are integers, then there is an optimal solution for which all $ x _ {ij } $ are integers (Dantzig's theorem on integral solutions of the transport problem).
In the assignment problem, for such a solution $ x _ {ij } $ is either zero or one; $ x _ {ij } = 1 $ means that person $ i $ is assigned to job $ j $; the weight $ c _ {ij } $ is the utility of person $ i $ assigned to job $ j $.
The special structure of the transport problem and the assignment problem makes it possible to use algorithms that are more efficient than the simplex method . Some of these use the Hungarian method (see, e.g., [a5] , [a1] , Chapt. 7), which is based on the König–Egervary theorem (see König theorem ), the method of potentials (see [a1] , [a2] ), the out-of-kilter algorithm (see, e.g., [a3] ) or the transportation simplex method.
In turn, the transportation problem is a special case of the network optimization problem.
A totally different assignment problem is the pole assignment problem in control theory.
| [a1] | D.B. Yudin, E.G. Gol'shtein, "Linear programming" , Israel Program Sci. Transl. (1965) (In Russian) |
| [a2] | R. Frisch, "La résolution des problèmes de programme linéaire par la méthode du potentiel logarithmique" , (1956) pp. 20–23 |
| [a3] | K. Murtz, "Linear and combinatorial programming" , Wiley (1976) |
| [a4] | M. Grötschel, L. Lovász, A. Schrijver, "Geometric algorithms and combinatorial optimization" , Springer (1987) |
| [a5] | C.H. Papadimitriou, K. Steiglitz, "Combinatorial optimization" , Prentice-Hall (1982) |
- This page was last edited on 5 April 2020, at 18:48.
- Privacy policy
- About Encyclopedia of Mathematics
- Disclaimers
- Impressum-Legal
Quadratic assignment problem
Author: Thomas Kueny, Eric Miller, Natasha Rice, Joseph Szczerba, David Wittmann (SysEn 5800 Fall 2020)
- 1 Introduction
- 2.1 Koopmans-Beckman Mathematical Formulation
- 2.2.1 Parameters
- 2.3.1 Optimization Problem
- 2.4 Computational Complexity
- 2.5 Algorithmic Discussions
- 2.6 Branch and Bound Procedures
- 2.7 Linearizations
- 3.1 QAP with 3 Facilities
- 4.1 Inter-plant Transportation Problem
- 4.2 The Backboard Wiring Problem
- 4.3 Hospital Layout
- 4.4 Exam Scheduling System
- 5 Conclusion
- 6 References
Introduction
The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957 [1] , is a mathematical optimization module created to describe the location of invisible economic activities. An NP-Complete problem, this model can be applied to many other optimization problems outside of the field of economics. It has been used to optimize backboards, inter-plant transportation, hospital transportation, exam scheduling, along with many other applications not described within this page.
Theory, Methodology, and/or Algorithmic Discussions
Koopmans-beckman mathematical formulation.
Economists Koopmans and Beckman began their investigation of the QAP to ascertain the optimal method of locating important economic resources in a given area. The Koopmans-Beckman formulation of the QAP aims to achieve the objective of assigning facilities to locations in order to minimize the overall cost. Below is the Koopmans-Beckman formulation of the QAP as described by neos-guide.org.
Quadratic Assignment Problem Formulation

Inner Product

Note: The true objective cost function only requires summing entries above the diagonal in the matrix comprised of elements

Since this matrix is symmetric with zeroes on the diagonal, dividing by 2 removes the double count of each element to give the correct cost value. See the Numerical Example section for an example of this note.
Optimization Problem
With all of this information, the QAP can be summarized as:

Computational Complexity
QAP belongs to the classification of problems known as NP-complete, thus being a computationally complex problem. QAP’s NP-completeness was proven by Sahni and Gonzalez in 1976, who states that of all combinatorial optimization problems, QAP is the “hardest of the hard”. [2]
Algorithmic Discussions
While an algorithm that can solve QAP in polynomial time is unlikely to exist, there are three primary methods for acquiring the optimal solution to a QAP problem:
- Dynamic Program
- Cutting Plane
Branch and Bound Procedures
The third method has been proven to be the most effective in solving QAP, although when n > 15, QAP begins to become virtually unsolvable.
The Branch and Bound method was first proposed by Ailsa Land and Alison Doig in 1960 and is the most commonly used tool for solving NP-hard optimization problems.
A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before one lists all of the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and the branch is eliminated if it cannot produce a better solution than the best one found so far by the algorithm.
Linearizations
The first attempts to solve the QAP eliminated the quadratic term in the objective function of

in order to transform the problem into a (mixed) 0-1 linear program. The objective function is usually linearized by introducing new variables and new linear (and binary) constraints. Then existing methods for (mixed) linear integer programming (MILP) can be applied. The very large number of new variables and constraints, however, usually poses an obstacle for efficiently solving the resulting linear integer programs. MILP formulations provide LP relaxations of the problem which can be used to compute lower bounds.
Numerical Example
Qap with 3 facilities.

| Permutation | Cost |
| (123) | 91.4 |
| 99.8 | |
| 98.4 | |
| 86.5 | |
| 103.3 | |
| 90 |

Applications
Inter-plant transportation problem.
The QAP was first introduced by Koopmans and Beckmann to address how economic decisions could be made to optimize the transportation costs of goods between both manufacturing plants and locations. [1] Factoring in the location of each of the manufacturing plants as well as the volume of goods between locations to maximize revenue is what distinguishes this from other linear programming assignment problems like the Knapsack Problem.
The Backboard Wiring Problem
As the QAP is focused on minimizing the cost of traveling from one location to another, it is an ideal approach to determining the placement of components in many modern electronics. Leon Steinberg proposed a QAP solution to optimize the layout of elements on a blackboard by minimizing the total amount of wiring required. [4]
When defining the problem Steinberg states that we have a set of n elements

as well as a set of r points

In his paper he derives the below formula:

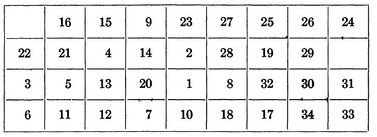
In his paper Steinberg a backboard with a 9 by 4 array, allowing for 36 potential positions for the 34 components that needed to be placed on the backboard. For the calculation, he selected a random initial placement of s1 and chose a random family of 25 unconnected sets.
The initial placement of components is shown below:

After the initial placement of elements, it took an additional 35 iterations to get us to our final optimized backboard layout. Leading to a total of 59 iterations and a final wire length of 4,969.440.
Hospital Layout
Building new hospitals was a common event in 1977 when Alealid N Elshafei wrote his paper on "Hospital Layouts as a Quadratic Assignment Problem". [5] With the high initial cost to construct the hospital and to staff it, it is important to ensure that it is operating as efficiently as possible. Elshafei's paper was commissioned to create an optimization formula to locate clinics within a building in such a way that minimizes the total distance that a patient travels within the hospital throughout the year. When doing a study of a major hospital in Cairo he determined that the Outpatient ward was acting as a bottleneck in the hospital and focused his efforts on optimizing the 17 departments there.
Elshafei identified the following QAP to determine where clinics should be placed:

For the Cairo hospital with 17 clinics, and one receiving and recording room bringing us to a total of 18 facilities. By running the above optimization Elshafei was able to get the total distance per year down to 11,281,887 from a distance of 13,973,298 based on the original hospital layout.
Exam Scheduling System
The scheduling system uses matrices for Exams, Time Slots, and Rooms with the goal of reducing the rate of schedule conflicts. To accomplish this goal, the “examination with the highest cross faculty student is been prioritized in the schedule after which the examination with the highest number of cross-program is considered and finally with the highest number of repeating student, at each stage group with the highest number of student are prioritized.” [6]

- ↑ 1.0 1.1 1.2 Koopmans, T., & Beckmann, M. (1957). Assignment Problems and the Location of Economic Activities. Econometrica, 25(1), 53-76. doi:10.2307/1907742
- ↑ 2.0 2.1 Quadratic Assignment Problem. (2020). Retrieved December 14, 2020, from https://neos-guide.org/content/quadratic-assignment-problem
- ↑ 3.0 3.1 3.2 Burkard, R. E., Çela, E., Pardalos, P. M., & Pitsoulis, L. S. (2013). The Quadratic Assignment Problem. https://www.opt.math.tugraz.at/~cela/papers/qap_bericht.pdf .
- ↑ 4.0 4.1 Leon Steinberg. The Backboard Wiring Problem: A Placement Algorithm. SIAM Review . 1961;3(1):37.
- ↑ 5.0 5.1 Alwalid N. Elshafei. Hospital Layout as a Quadratic Assignment Problem. Operational Research Quarterly (1970-1977) . 1977;28(1):167. doi:10.2307/300878
- ↑ 6.0 6.1 Muktar, D., & Ahmad, Z.M. (2014). Examination Scheduling System Based On Quadratic Assignment.
Navigation menu
OPERATIONS RESEARCH
Lesson 8. introduction and mathematical formulation.
Current course
Assignment Problem: Linear Programming
The assignment problem is a special type of transportation problem , where the objective is to minimize the cost or time of completing a number of jobs by a number of persons.
In other words, when the problem involves the allocation of n different facilities to n different tasks, it is often termed as an assignment problem.
The model's primary usefulness is for planning. The assignment problem also encompasses an important sub-class of so-called shortest- (or longest-) route models. The assignment model is useful in solving problems such as, assignment of machines to jobs, assignment of salesmen to sales territories, travelling salesman problem, etc.
It may be noted that with n facilities and n jobs, there are n! possible assignments. One way of finding an optimal assignment is to write all the n! possible arrangements, evaluate their total cost, and select the assignment with minimum cost. But, due to heavy computational burden this method is not suitable. This chapter concentrates on an efficient method for solving assignment problems that was developed by a Hungarian mathematician D.Konig.
"A mathematician is a device for turning coffee into theorems." -Paul Erdos
Formulation of an assignment problem
Suppose a company has n persons of different capacities available for performing each different job in the concern, and there are the same number of jobs of different types. One person can be given one and only one job. The objective of this assignment problem is to assign n persons to n jobs, so as to minimize the total assignment cost. The cost matrix for this problem is given below:
The structure of an assignment problem is identical to that of a transportation problem.
To formulate the assignment problem in mathematical programming terms , we define the activity variables as
| x = | 1 if job j is performed by worker i | |
| 0 otherwise |
for i = 1, 2, ..., n and j = 1, 2, ..., n
In the above table, c ij is the cost of performing jth job by ith worker.
Generalized Form of an Assignment Problem
The optimization model is
Minimize c 11 x 11 + c 12 x 12 + ------- + c nn x nn
subject to x i1 + x i2 +..........+ x in = 1 i = 1, 2,......., n x 1j + x 2j +..........+ x nj = 1 j = 1, 2,......., n
x ij = 0 or 1
In Σ Sigma notation
x ij = 0 or 1 for all i and j
An assignment problem can be solved by transportation methods, but due to high degree of degeneracy the usual computational techniques of a transportation problem become very inefficient. Therefore, a special method is available for solving such type of problems in a more efficient way.
Assumptions in Assignment Problem
- Number of jobs is equal to the number of machines or persons.
- Each man or machine is assigned only one job.
- Each man or machine is independently capable of handling any job to be done.
- Assigning criteria is clearly specified (minimizing cost or maximizing profit).
Share this article with your friends
Operations Research Simplified Back Next
Goal programming Linear programming Simplex Method Transportation Problem
Assignment problem
1 formulation of the problem, 2 variants of the problem, 3 algorithms for solving the problem, 4 references.
Suppose that there are [math]n[/math] agents and [math]m[/math] tasks, which can be distributed between these agents. Only one task can be assigned to each agent, and each task can be assigned to only one agent. The cost of assignment of the [math]i[/math] -th task to the [math]j[/math] -th agent is [math]c(i, j)[/math] . If [math]c(i, j) = \infty[/math] , then the [math]i[/math] -th task cannot be assigned to the [math]j[/math] -th agent.
The assignment problem : find a feasible set of assignments [math]A = \{ (i_1, j_1), \ldots, (i_k, j_k) \}[/math] , [math]k = \min \{m, n\}[/math] having the maximum total cost:
If [math]m = n[/math] , then we say of the linear assignment problem : each agent is assigned to perform exactly one task, and each task is assigned to exactly one agent.
In the case of unit weights, we have to find a maximum matching in a bipartite graph, and the problem reduces to assigning as much tasks as possible.
- The Hungarian Method [1] [2] [3] for the linear problem. The complexity is [math]O(n^4)[/math] (and can be reduced [4] to [math]O(n^3)[/math] );
- the auction algorithm [5] [6] ;
- the Hopcroft-Karp algorithm [7] for the problem with unit weights. The complexity is [math]O(m \sqrt{n})[/math] .
- ↑ Kuhn, H W. “The Hungarian Method for the Assignment Problem.” Naval Research Logistics Quarterly 2, no. 1 (March 1955): 83–97. doi:10.1002/nav.3800020109.
- ↑ Kuhn, H W. “Variants of the Hungarian Method for Assignment Problems.” Naval Research Logistics Quarterly 3, no. 4 (December 1956): 253–58. doi:10.1002/nav.3800030404.
- ↑ Munkres, James. “Algorithms for the Assignment and Transportation Problems.” Journal of the Society for Industrial and Applied Mathematics 5, no. 1 (March 1957): 32–38. doi:10.1137/0105003.
- ↑ Tomizawa, N. “On Some Techniques Useful for Solution of Transportation Network Problems.” Networks 1, no. 2 (1971): 173–94. doi:10.1002/net.3230010206.
- ↑ Bertsekas, Dimitri P. “Auction Algorithms for Network Flow Problems: a Tutorial Introduction.” Computational Optimization and Applications 1 (1992): 7–66.
- ↑ Zavlanos, Michael M, Leonid Spesivtsev, and George J Pappas. “A Distributed Auction Algorithm for the Assignment Problem,” Proceedings of IEEE CDC'08, 1212–17, IEEE, 2008. doi:10.1109/CDC.2008.4739098.
- ↑ Hopcroft, John E, and Richard M Karp. “An $N^{5/2} $ Algorithm for Maximum Matchings in Bipartite Graphs.” SIAM Journal on Computing 2, no. 4 (1973): 225–31. doi:10.1137/0202019.
- Problem level
- Articles in progress
Navigation menu
Personal tools.
- Create account
- View source
- View history
- Recent changes
File storage
- Upload file
- What links here
- Related changes
- Special pages
- Printable version
- Permanent link
- Page information
- This page was last edited on 6 March 2018, at 17:08.
- Content is available under Creative Commons Attribution unless otherwise noted.
- Privacy policy
- About Algowiki
- Disclaimers
Please enable JavaScript to pass antispam protection! Here are the instructions how to enable JavaScript in your web browser http://www.enable-javascript.com . Antispam by CleanTalk.
Your Article Library
Assignment problem in linear programming : introduction and assignment model.
ADVERTISEMENTS:
Assignment problem is a special type of linear programming problem which deals with the allocation of the various resources to the various activities on one to one basis. It does it in such a way that the cost or time involved in the process is minimum and profit or sale is maximum. Though there problems can be solved by simplex method or by transportation method but assignment model gives a simpler approach for these problems.
In a factory, a supervisor may have six workers available and six jobs to fire. He will have to take decision regarding which job should be given to which worker. Problem forms one to one basis. This is an assignment problem.
1. Assignment Model :
Suppose there are n facilitates and n jobs it is clear that in this case, there will be n assignments. Each facility or say worker can perform each job, one at a time. But there should be certain procedure by which assignment should be made so that the profit is maximized or the cost or time is minimized.
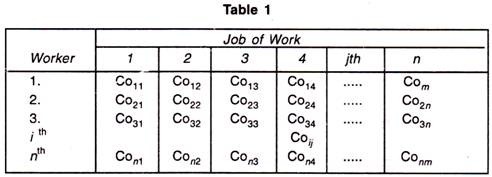
In the table, Co ij is defined as the cost when j th job is assigned to i th worker. It maybe noted here that this is a special case of transportation problem when the number of rows is equal to number of columns.
Mathematical Formulation:
Any basic feasible solution of an Assignment problem consists (2n – 1) variables of which the (n – 1) variables are zero, n is number of jobs or number of facilities. Due to this high degeneracy, if we solve the problem by usual transportation method, it will be a complex and time consuming work. Thus a separate technique is derived for it. Before going to the absolute method it is very important to formulate the problem.
Suppose x jj is a variable which is defined as
1 if the i th job is assigned to j th machine or facility
0 if the i th job is not assigned to j th machine or facility.
Now as the problem forms one to one basis or one job is to be assigned to one facility or machine.

The total assignment cost will be given by
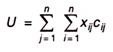
The above definition can be developed into mathematical model as follows:
Determine x ij > 0 (i, j = 1,2, 3…n) in order to
Subjected to constraints

and x ij is either zero or one.
Method to solve Problem (Hungarian Technique):
Consider the objective function of minimization type. Following steps are involved in solving this Assignment problem,
1. Locate the smallest cost element in each row of the given cost table starting with the first row. Now, this smallest element is subtracted form each element of that row. So, we will be getting at least one zero in each row of this new table.
2. Having constructed the table (as by step-1) take the columns of the table. Starting from first column locate the smallest cost element in each column. Now subtract this smallest element from each element of that column. Having performed the step 1 and step 2, we will be getting at least one zero in each column in the reduced cost table.
3. Now, the assignments are made for the reduced table in following manner.
(i) Rows are examined successively, until the row with exactly single (one) zero is found. Assignment is made to this single zero by putting square □ around it and in the corresponding column, all other zeros are crossed out (x) because these will not be used to make any other assignment in this column. Step is conducted for each row.
(ii) Step 3 (i) in now performed on the columns as follow:- columns are examined successively till a column with exactly one zero is found. Now , assignment is made to this single zero by putting the square around it and at the same time, all other zeros in the corresponding rows are crossed out (x) step is conducted for each column.
(iii) Step 3, (i) and 3 (ii) are repeated till all the zeros are either marked or crossed out. Now, if the number of marked zeros or the assignments made are equal to number of rows or columns, optimum solution has been achieved. There will be exactly single assignment in each or columns without any assignment. In this case, we will go to step 4.
4. At this stage, draw the minimum number of lines (horizontal and vertical) necessary to cover all zeros in the matrix obtained in step 3, Following procedure is adopted:
(iii) Now tick mark all the rows that are not already marked and that have assignment in the marked columns.
(iv) All the steps i.e. (4(i), 4(ii), 4(iii) are repeated until no more rows or columns can be marked.
(v) Now draw straight lines which pass through all the un marked rows and marked columns. It can also be noticed that in an n x n matrix, always less than ‘n’ lines will cover all the zeros if there is no solution among them.
5. In step 4, if the number of lines drawn are equal to n or the number of rows, then it is the optimum solution if not, then go to step 6.
6. Select the smallest element among all the uncovered elements. Now, this element is subtracted from all the uncovered elements and added to the element which lies at the intersection of two lines. This is the matrix for fresh assignments.
7. Repeat the procedure from step (3) until the number of assignments becomes equal to the number of rows or number of columns.
Related Articles:
- Two Phase Methods of Problem Solving in Linear Programming: First and Second Phase
- Linear Programming: Applications, Definitions and Problems
No comments yet.
Leave a reply click here to cancel reply..
You must be logged in to post a comment.
Quadratic Assignment Problem
- Reference work entry
- pp 3119–3149
- Cite this reference work entry

- Leonidas Pitsoulis 3 &
- Panos M. Pardalos 4
932 Accesses
6 Citations
Article Outline
Formulations
Linearizations
Lawler's Linearization
Kaufman–Broeckx Linearization
Frieze–Yadegar Linearization
Adams–Johnson Linearization
Complexity Issues
Computational Complexity
PLS-Complexity
Asymptotic Behavior
Polynomially Solvable Cases
Lower Bounds
Gilmore–Lawler Type Lower Bounds
Variance Reduction Lower Bounds
Eigenvalue Based Lower Bounds
Bounds Based on Semidefinite Relaxations
Exact Solution Methods
Branch and Bound
Traditional Cutting Plane Methods
Polyhedral Cutting Planes
Construction Methods
Limited Enumeration Methods
Improvement Methods
Tabu Search
Simulated Annealing
Genetic Algorithms
Greedy Randomized Adaptive Search Procedure
Ant Systems
Related Problems
Biquadratic Assignment Problem
Multidimensional Assignment Problems
Bottleneck QAP
Other Problems Which Can Be Formulated As QAPs
QAP Problem Generators
Surveys and Books
This is a preview of subscription content, log in via an institution to check access.

Access this chapter
Subscribe and save.
- Get 10 units per month
- Download Article/Chapter or Ebook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
- Available as PDF
- Read on any device
- Instant download
- Own it forever
- Durable hardcover edition
- Dispatched in 3 to 5 business days
- Free shipping worldwide - see info
Tax calculation will be finalised at checkout
Purchases are for personal use only
Institutional subscriptions
Similar content being viewed by others

Quadratic Assignment Problems
A linear formulation with $$o(n^2)$$ variables for quadratic assignment problems with manhattan distance matrices, binary unconstrained quadratic optimization problem.
Aarts E, Lenstra JK (eds) (1997) Local search in combinatorial optimization. Wiley, New York
MATH Google Scholar
Adams WP, Johnson TA (1994) Improved linear programming-based lower bounds for the quadratic assignment problem. In: Pardalos PM, Wolkowicz H (eds) Quadratic Assignment and Related Problems. DIMACS. Amer. Math. Soc., Providence, pp 43–75
Google Scholar
Adams WP, Sherali HD (1986) A tight linearization and an algorithm for zero-one quadratic programming problems. Managem Sci 32(10):1274–1290
MATH MathSciNet Google Scholar
Adams WP, Sherali HD (1990) Linearization strategies for a class of zero-one mixed integer programming problems. Oper Res 38(2):217–226
Ahuja RK, Orlin JB, Tivari A (1995) A greedy genetic algorithm for the quadratic assignment problem. Techn Report 3826-95, Sloan School Management
Arora S, Frieze A, Kaplan H (1996) A new rounding procedure for the assignment problem with applications to dense graph arrangement problems. In: Proc. 37-th Annual IEEE Symp. Foundations of Computer Sci. (FOCS). IEEE, New York, pp 21–30
Balas E, Mazzola JB (1980) Quadratic 0-1 programming by a new linearization. In: Proc TIMS/ORSA, May 1980
Balas E, Mazzola JB (1984) Nonlinear programming: I. Linearization techniques. Math Program 30:1–21
Article MATH MathSciNet Google Scholar
Balas E, Mazzola JB (1984) Nonlinear programming: II. Dominance relations and algorithms. Math Program 30:22–45
Balas E, Qi L (1993) Linear-time separation algorithms for the three-index assignment polytope. Discrete Appl Math (1993):1–12
Balas E, Saltzman MJ (1989) Facets of the three-index assignment polytope. Discrete Appl Math (1989):201–229
Battiti R, Tecchiolli G (1994) The reactive tabu search. ORSA J Comput (1994):126–140
Bazaraa MS, Sherali HD (1980) Bender's partitioning scheme applied to a new formulation of the quadratic assignment problem. Naval Res Logist Quart 27:29–41
Bazaraa MS, Sherali HD (1982) On the use of exact and heuristic cutting plane methods for the quadratic assignment problem. J Oper Res Soc 33:991–1003
Birkoff G (1946) Tres observaciones sobre el algebra lineal. Univ Nac Tucuman Rev (A):147–151
Bollobás B (1978) Extremal graph theory. Acad. Press, New York
Buffa ES, Armour GC, Vollmann TE (1962) Allocating facilities with CRAFT. Harvard Business Rev 42:136–158
Burkard RE (1973) Die Störungsmethode zur Lösung quadratischer Zuordnungsprobleme. Oper Res Verfahren 16:84–108
Burkard RE (1974) Quadratische Bottleneckprobleme. Oper Res Verfahren 18:26–41
MathSciNet Google Scholar
Burkard RE (1991) Locations with spatial interactions: the quadratic assignment problem. In: Mirchandani PB, Francis RL (eds) Discrete Location Theory. Wiley, New York
Burkard RE, Bönniger T (1983) A heuristic for quadratic Boolean programs with applications to quadratic assignment problems. Europ J Oper Res 13:374–386
Article MATH Google Scholar
Burkard RE, Çela E (1995) Heuristics for biquadratic assignment problems and their computational comparison. Europ J Oper Res 83:283–300
Burkard RE, Çela E, Demidenko VM, Metelski NN, Woeginger GJ (1997) Perspectives of easy and hard cases of the quadratic assignment problems. Techn Report SFB 104, Techn Univ Graz
Burkard RE, Çela E, Klinz B (1994) On the biquadratic assignment problem. In: Pardalos PM, Wolkowicz H (eds) Quadratic assignment and related problems. DIMACS. Amer. Math. Soc., Providence, pp 117–146
Burkard RE, Çela E, Pardalos PM, Pitsoulis LS (1998) The quadratic assignment problem. In: Du D-Z and Pardalos PM (eds) Handbook Combinatorial Optim., vol 3. Kluwer, Dordrecht, pp 241–337
Burkard RE, Çela E, Rote G, Woeginger GJ (1995) The quadratic assignment problem with an Anti-Monge and a Toeplitz matrix: Easy and hard cases. Techn Report SFB 34, Techn Univ Graz
Burkard RE, Fincke U (1982) On random quadratic bottleneck assignment problems. Math Program 23:227–232
Burkard RE, Fincke U (1983) The asymptotic probabilistic behaviour of quadratic sum assignment problems. Z Oper Res 27:73–81
Burkard RE, Fincke U (1985) Probabilistic asymptotic properties of some combinatorial optimization problems. Discrete Appl Math 12:21–29
Burkard RE, Hahn W, Zimmermann U (1977) An algebraic approach to assignment problems. Math Program 12:318–327
Burkard RE, Karisch S, Rendl F (1997) QAPLIB – Aquadratic assignment problem library. J Global Optim 10:391–403
Burkard RE, Klinz B, Rudolf R (1996) Perspectives of Monge properties in optimization. Discrete Appl Math 70:95–161
Burkard RE, Rendl F (1984) A thermodynamically motivated simulation procedure for combinatorial optimization problems. Europ J Oper Res 17:169–174
Burkard RE, Zimmermann U (1982) Combinatorial optimization in linearly ordered semimodules: A survey. Modern Applied Mathematics. North-Holland, Amsterdam, pp 392–436
Çela E (1998) The quadratic assignment problem: Theory and algorithms. Kluwer, Dordrecht
Chakrapani J, Skorin-Kapov J (1993) Massively parallel tabu search for the quadratic assignment problem. Ann Oper Res 41:327–342
Christofides N (1976) Worst case analysis of a new heuristic for the traveling salesman problem. Grad School Industr Admin Carnegie-Mellon Univ 338
Colorni A, Dorigo M, Maniezzo V (1996) The ant system: optimization by a colony of cooperating agents. IEEE Trans Syst, Man Cybern Part B 26:29–41
Article Google Scholar
Colorni A, Maniezzo V (1998) The ant system applied to the quadratic assignment problem. IEEE Trans Knowledge and Data Enginto
Connolly DT (1990) An improved annealing scheme for the QAP. Europ J Oper Res 46:93–100
Conrad K (1971) Das quadratische Zuweisungsproblem und zwei seiner Spezialfalle. Mohr-Siebeck, Tübingen
Cyganski D, Vaz RF, Virball VG (1994) Quadratic assignment problems with the Palubeckis' algorithm are degenerate. IEEE Trans Circuits and Systems I 41:481–484
Article MathSciNet Google Scholar
Davis L (1987) Genetic algorithms and simulated annealing. Pitman, Boston
Deneko VG, Woeginger GJ (1996) A solvable case of the quadratic assignment problem. Techn Report SFB 88,Inst Math, Techn Univ Graz
Dorigo M (1992) Optimization, learning, and natural algorithms. PhD Thesis, Dip. Elettronica e Informazione Politecn. Milano. (In Italian)
Dyer ME, Frieze AM, McDiarmid CJH (1986) On linear programs with random costs. Math Program 35:3–16
Edwards CS (1980) A branch and bound algorithm for the Koopmans–Beckman quadratic assignment problem. Math Program Stud 13:35–52
Feo TA, Resende MGC (1995) Greedy randomized adaptive search procedures. J Global Optim 6:109–133
Feo TA, Resende MGC, Smith SH (1994) A greedy randomized adaptive search procedure for maximum independent set. Oper Res 42:860–878
Finke G, Burkard RE, Rendl F (1984) Eigenvalue approach to quadratic assignment problems. In: 5th Symp. Oper. Res., 1984
Finke G, Burkard RE, Rendl F (1987) Quadratic assignment problems. Ann Discret Math 31:61–82
Fleurent C, Ferland J (1994) Genetic hybrids for the quadratic assignment problem. In: Pardalos PM, Wolkowicz H (eds) Quadratic assignment and related problems. DIMACS. Amer. Math. Soc., Providence pp 43–75
Floudas CA, Pardalos PM (1990) A collection of test problems for constrained global optimization algorithms. Lecture Notes Computer Sci, vol 455. Springer, Berlin
Frenk JCB, van Houweninge M and, Rinnooy Kan AHG (1985) Asymptotic properties of assignment problems. Math Oper Res 10:100–116
Frieze AM (1974) A bilinear programming formulation of the 3-dimensional assignment problem. Math Program 7:376–379
Frieze AM, Yadegar J (1983) On the quadratic assignment problem. Discrete Appl Math 5:89–98
Gambardella LM, Taillard ED, Dorigo M (1997) Ant colonies for the QAP. Techn Report IDSIA-4-97, Ist dalle Molle Di Studi sull'Intelligenza Artificiale Lugano
Garey MR, Johnson DS (1979) Computers and intractability: A guide to the theory of NP-completeness. Freeman, New York
Gavett JW, Plyter NV (1966) The optimal assignment of facilities to locations by branch and bound. Oper Res 14:210–232
Gilmore PC (1962) Optimal and suboptimal algorithms for the quadratic assignment problem. SIAM J Appl Math 10:305–313
(1993) Tabu search. Ann Oper Res 41
Glover F (1989) Tabu search – Part I. ORSA J Comput 1:190–206
Glover F (1990) Tabu search – Part II. ORSA J Comput 2:4–32
Goldberg DE (1989) Genetic algorithms in search, optimization, and machine learning. Addison-Wesley, Reading
Hadley SW (1989) Continuous optimization approaches for the quadratic assignment problem. PhD Thesis, Univ. Waterloo
Hadley SW, Rendl F, Wolkowicz H (1990) Bounds for the quadratic assignment problem using continuous optimization techniques. Integer Programming and Combinatorial Optimization. Univ. Waterloo Press, Waterloo, pp 237–248
Hadley SW, Rendl F, Wolkowicz H (1992) A new lower bound via projection for the quadratic assignment problem. Math Oper Res 17(3):727–739
Hadley SW, Rendl F, Wolkowicz H (1992) Nonsymmetric quadratic assignment problems and the Hoffman–Wielandt Inequality. Linear Alg & its Appl 58:109–124
Hardy GG, Littlewood JE, Polya G (1952) Inequalities. Cambridge Univ. Press, Cambridge
Heider CH (1972) A computationally simplified pair exchange algorithm for the quadratic assignment problem. Paper 101, Center Naval Anal, Arlington
Jansen B (1993) A note on lower bounds for the QAP. Techn Report (dec), Delft Univ Techn Math and Computer Sci
Johnson DS, Papadimitriou CH, Yannakakis M (1988) How easy is local search? J Comput Syst Sci 37:79–100
Johnson TA (1992) New linear programming-based solution procedures for the quadratic assignment problem. PhD Thesis, Clemson Univ.
Jünger M (1985) Polyhedral combinatorics and the acyclic subdigraph problem. Heldermann, Berlin
Kaibel V (1997) Polyhedral combinatorics of the quadratic assignment problem. PhD Thesis, Univ. Köln
Karisch SE (1995) Nonlinear approaches for quadratic assignment and graph partition problems. PhD Thesis, Techn. Univ. Graz
Karisch SE, Rendl F, Wolkowicz H, Zhao Q (1998) Semidefinite programming relaxations for the quadratic assignment problem. J Combin Optim 2(1):71–109
Karisch SE, Rendl F, Wolkowicz H (1994) Trust regions and the quadratic assignment problem. In: Pardalos PM, Wolkowicz H (eds) Quadratic assignment and related problems. DIMACS. Amer. Math. Soc., Providence, pp 199–220
Karp R (1972) Reducibility among combinatorial problems. In: Miller RE, Thatcher JW (eds) Proc. Complexity of Computer Computations. Plenum, New York, pp 85–104
Kaufman L, Broeckx F (1978) An algorithm for the quadratic assignment problem using Benders' decomposition. Europ J Oper Res 2:204–211
Kernighan B, Lin S (1972) An efficient heuristic procedure for partitioning graphs. Bell Systems J 49:291–307
Kirkpatrick S, Gelatt CD, Vecchi MP (1983) Optimization by simulated annealing. Science 220:671–680
Klincewicz JG (1992) Avoiding local optima in the p-hub location problem using tabu search and GRASP. Ann Oper Res 40:283–302
Klincewicz JG, Rajan A (1992) Using GRASPto solve the component grouping problem. Techn Report, AT&T Bell Lab
Koopmans TC, Beckmann MJ (1957) Assignment problems and the location of economic activities. Econometrica 25:53–76
Land AM (1963) A problem of assignment with interrelated costs. Oper Res Quart 14:185–198
Laporte G, Mercure H (1988) Balancing hydraulic turbine runners: A quadratic assignment problem. Europ J Oper Res 35:378–382
Lawler EL (1963) The quadratic assignment problem. Managem Sci 9:586–599
Lawler EL, Lenstra JK, Rinnooy Kan AHG, Shmoys DB (1985) The traveling salesman problem: A guided tour of combinatorial optimization. Wiley, New York
Lengauer T (1990) Combinatorial algorithms for intergrated circuit layout. Wiley, New York
Leontief W (1966) Input–output economics. Oxford Univ. Press, Oxford
Li Y, Pardalos PM (1992) Generating quadratic assignment test problems with known optimal permutations. Comput Optim Appl 1(2):163–184
Li Y, Pardalos PM, Ramakrishnan KG, Resende MGC (1994) Lower bounds for the quadratic assignment problem. Ann Oper Res 50:387–410
Li Y, Pardalos PM, Resende MGC (1994) A greedy randomized adaptive search procedure for the quadratic assignment problem. In: Pardalos PM, Wolkowicz H (eds) Quadratic assignment and related problems. DIMACS 16. Amer. Math. Soc., Providence, pp 237–261
Mavridou T, Pardalos PM, Pitsoulis LS, Resende MGC (1998) A GRASPfor the biquadratic assignment problem. Europ J Oper Res 105(3):613–621
Metropolis N, Rosenbluth A, Rosenbluth M, Teller A, Teller E (1953) Equations of state calculations by fast computing machines. J Chem Phys 21:1087–1092
Mirchandani PB, Obata T (1979) Locational decisions with interactions between facilities: the quadratic assignment problem a review. Working Paper May Ps-79-1, Rensselaer Polytechnic Inst, Troy, New York
Mirsky L (1956) The spread of a matrix. Mathematika 3:127–130
Mosevich J (1986) Balancing hydraulic turbine runners – a discrete combinatorial optimization problem. Europ J Oper Res 26:202–204
Muller-Merbach H (1970) Optimale Reihenlorgen. Springer, Berlin
Murphey RA, Pardalos PM, Pitsoulis L (1997) A greedy randomized adaptive search procedure for the multitarget multisensor tracking problem. In: Pardalos PM, Du D-Z (eds) Network Design: Connectivity and Facility Location. DIMACS 40. Amer. Math. Soc., Providence, pp 277–302
Murphey RA, Pardalos PM, Pitsoulis L (1998) A parallel GRASP for the data association multidimensional assignment problem. Parallel Processing of Discrete Problems. In: IMA vol Math Appl, vol 106. Springer, Berlin, pp 159–180
Murthy KA, Pardalos PM, Li Y (1992) A local search algorithm for the quadratic assignment problem. Informatica 3(4):524–538
Murty KG (1968) An algorithm for ranking all the assignments in order of increasing cost. Oper Res 16:682–287
Nugent CE, Vollmann TE, Ruml J (1969) An experimental comparison of techniques for the assignment of facilities to locations. J Oper Res 16:150–173
Padberg MW, Rijal MP (1996) Location, scheduling, design and integer programming. Kluwer, Dordrecht
Palubetskis GS (1988) Generation of quadratic assignment test problems with known optimal solutions. Zh Vychisl Mat Mat Fiz 28(11):1740–1743. (In Russian.)
Papadimitriou CH, Wolfe D (1985) The complexity of facets resolved. In: Proc Foundations Computer Sci, pp 74–78
Pardalos PM, Pitsoulis LS, Resende MGC (1995) A parallel GRASP implementation for solving the quadratic assignment problem. In: Ferreira A and Rolim JDP (eds) Parallel Algorithms for Irregular Problems: State of the Art. Kluwer, Dordrecht, pp 115–133
Pardalos PM, Pitsoulis LS, Resende MGC (1997) Algorithm 769: FORTRAN subroutines for approximate solution of sparse quadratic assignment problems. ACM Trans Math Softw 23:196–208
Pardalos PM, Ramakrishnan KG, Resende MGC, Li Y (1997) Implementation of a variable reduction based lower bound in a branch and bound algorithm for the quadratic assignment problem. SIAM J Optim 7(1):280–294
Pardalos PM, Rendl F, Wolkowicz H (1994) The quadratic assignment problem: A survey and recent developments. In: Pardalos PM, Wolkowicz H (eds) Quadratic assignment and related problems. DIMACS vol 16. Amer. Math. Soc., Providence, pp 1–42
Pardalos PM, Wolkowicz H (1994) Quadratic assignment and related problems. DIMACS, vol 16. Amer. Math. Soc., Providence
Pardalos PM, Xue Jue (1994) The maximum clique problem. J Global Optim 4:301–328
Pierskalla WP (1967) The tri-substitution method for the three-multidimensional assignment problem. CORS J 5:71–81
Pierskalla WP (1968) The multidimensional assignment problem. Oper Res 16:422–431
Pitsoulis LS (1998) Algorithms for nonlinear assignment problems. PhD Thesis, Dept. Industr. Systems Engin., Univ. Florida
Poore AB, Rijavec N (1994) Partitioning multiple data sets: multidimensional assignments and Lagrangian relaxation. In: Pardalos PM, Wolkowicz H (eds) Quadratic assignment and related problems. DIMACS vol 16. Amer. Math. Soc., Providence, pp 317–342
Pusztaszeri J, Rensing PE, Liebling TM (1995) Tracking elementary particles near their primary vertex: A combinatorial approach. J Global Optim 16:422–431
Qi L, Balas E, Gwan G (1994) A new facet class and a polyhedral method for the three-index assignment problem. In: Du D-Z (ed) Advances in Optimization. Kluwer, Dordrecht, pp 256–274
Queyranne M (1986) Performance ratio of heuristics for triangle inequality quadratic assignment problems. Oper Res Lett 4:231–234
Reinelt G (1985) The linear ordering problem: Algorithms and applications Res and Exposition in Math, vol 8. Heldermann, Berlin
Rendl F (1985) Ranking scalar products to improve bounds for the quadratic assignment problem. Europ J Oper Res 20:363–372
Rendl F, Wolkowicz H (1992) Applications of parametric programming and eigenvalue maximization to the quadratic assignment problem. Math Program 53:63–78
Resende MGC, Pitsoulis LS, Pardalos PM (1997) Approximate solution of weighted MAX-SAT problems using GRASP. In: Pardalos PM Resende MGC, Du DZ (eds) The Satisfiability Problem. DIMACS vol 35. Amer. Math. Soc., Providence, pp 393–405
Rhee WT (1989) A note on asymptotic properties of the quadratic assigment problem. Oper Res Lett 4:197–200
Rhee WT (1991) Stochastic analysis of the quadratic assignment problem. Math Oper Res 2:223–239
Roucairol C (1979) A reduction method for quadratic assignment problems. Oper Res Verfahren 32:183–187
Sahni S, Gonzalez T (1976) P-complete approximation problems. J ACM 23:555–565
Schäffer AA, Yannakakis M (1991) Simple local search problems that are hard to solve. SIAM J Comput 20:56–87
Skorin-Kapov J (1990) Tabu search applied to the quadratic assignment problem. ORSA J Comput 2(1):33–45
Szpankowski W (1995) Combinatorial optimization problems for which almost every algorithm is asymptotically optimal! Optim 33:359–367
Taillard E (1991) Robust tabu search for the quadratic assignment problem. Parallel Comput 17:443–455
Tate DM, Smith AE (1995) A genetic approach to the quadratic assignment problem. Comput Oper Res 22:73–83
Ĉerný V (1985) Thermodynamical approach to the traveling salesman problem: An efficient simulation algorithm. J Optim Th Appl 45:41–51
Wilhelm MR, Ward TL (1987) Solving quadratic assignment problems by simulated annealing. IEEE Trans 19(1):107–119
Zhao Q (1996) Semidefinite programming for assignment and partitioning problems. PhD Thesis, Univ. Waterloo
Download references
Author information
Authors and affiliations.
Princeton University, Princeton, USA
Leonidas Pitsoulis
Center for Applied Optim. Department Industrial and Systems Engineering, University Florida, Gainesville, USA
Panos M. Pardalos
You can also search for this author in PubMed Google Scholar
Editor information
Editors and affiliations.
Department of Chemical Engineering, Princeton University, Princeton, NJ, 08544-5263, USA
Christodoulos A. Floudas
Center for Applied Optimization, Department of Industrial and Systems Engineering, University of Florida, Gainesville, FL, 32611-6595, USA
Rights and permissions
Reprints and permissions
Copyright information
© 2008 Springer-Verlag
About this entry
Cite this entry.
Pitsoulis, L., Pardalos, P.M. (2008). Quadratic Assignment Problem . In: Floudas, C., Pardalos, P. (eds) Encyclopedia of Optimization. Springer, Boston, MA. https://doi.org/10.1007/978-0-387-74759-0_534
Download citation
DOI : https://doi.org/10.1007/978-0-387-74759-0_534
Publisher Name : Springer, Boston, MA
Print ISBN : 978-0-387-74758-3
Online ISBN : 978-0-387-74759-0
eBook Packages : Mathematics and Statistics Reference Module Computer Science and Engineering
Share this entry
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Publish with us
Policies and ethics
- Find a journal
- Track your research
Assignment Problem
- Feb 20, 2024
The assignment problem is a special case of transportation problem.
Suppose there are $n$ jobs to be performed and $n$ persons are available for these jobs. Assume that each person can do each job at a time, though with varying degree of efficiency.
Let $c_{ij}$ be the cost if the $i^{th}$ person is assigned the $j^{th}$ job. Then the problem is to find an assignment so that the total cost of performing all jobs is minimum. (i.e., which job should be assigned to which person with minimum cost). Such problem is called an Assignment Problem (AP).
The tabular form of the assignment problem is as follows
| Persons \ Jobs | $1$ | $2$ | $\cdots$ | $j$ | $\cdots$ | $n$ |
|---|---|---|---|---|---|---|
| Persons/ Jobs | $1$ | $2$ | $\cdots$ | $j$ | $\cdots$ | $n$ |
| $1$ | $c_{11}$ | $c_{12}$ | $\cdots$ | $c_{1j}$ | $\cdots$ | $c_{1n}$ |
| $2$ | $c_{21}$ | $c_{22}$ | $\cdots$ | $c_{2j}$ | $\cdots$ | $c_{2n}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ |
| $i$ | $c_{i1}$ | $c_{i2}$ | $\cdots$ | $c_{ij}$ | $\cdots$ | $c_{in}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ |
| $n$ | $c_{n1}$ | $c_{n2}$ | $\cdots$ | $c_{nj}$ | $\cdots$ | $c_{nn}$ |
The above table is called the $n\times n$ cost-matrix, where $c_{ij}$ are real numbers.
Thus the objective in the Assignment Problem is to assign a number of jobs to the equal number of persons at a minimum cost or maximum profit. e.g. assigning men to offices, classes to rooms, drivers to trucks, problems to research teams etc.
Mathematical Formulation of AP
Mathematically, the AP can be stated as $$ \begin{equation}\label{eq2.4} \min z = \sum_{i=1}^n\sum_{j=1}^n x_{ij} c_{ij}. \end{equation} $$ subject to $$ \begin{equation}\label{eq2.5} \sum_{j=1}^n x_{ij} =1,; \text{ for } i=1,2,\ldots, n \end{equation} $$
$$ \begin{equation}\label{eq2.6} \sum_{i=1}^n x_{ij} =1,; \text{ for } j=1,2,\ldots,n \end{equation} $$ where $$ \begin{equation*} x_{ij}=\left{ \begin{array}{ll} 1, & \hbox{if $i^{th}$ person is assigned $j^{th}$ job;} \ 0, & \hbox{otherwise.} \end{array} \right. \end{equation*} $$ Constraint \eqref{eq2.5} indicate that one job is done by $i^{th}$ person $i=1,2,\ldots, n$ and constraint \eqref{eq2.6} indicate that one person should be assigned $j^{th}$ job $j=1,2,\ldots, n$.
It may be observed from the above formulation that AP is a special type of Linear programming problem.
Unbalanced Assignment Problem
If the cost matrix of an assignment problem is not a square matrix, the assignment problem is called an Unbalanced Assignment Problem . In such a case, add dummy row or dummy column with zero cost in the cost matrix so as to form a square matrix. Then apply the usual assignment method to find the optimal solution.
Maximal Assignment Problem
Sometimes, the assignment problem deals with the maximization of an objective function instead of minimization.. For example, it may be required to assign persons to jobs in such a way that the expected profit is maximum. In such a case, first convert the problem of maximization to minimization and apply the usual procedure of assignment.
The assignment problem of maximization type can be converted to minimization type by subtracting all the elements of the given profit matrix from the largest element.
Restrictions on Assignment
Sometimes due to technical or other difficulties do not permit the assignment of a particular facility to a particular job. In such a situation, the difficulty can be overcome by assigning a very high cost (say, infinity i.e. $\infty$) to the corresponding cell.
Because of assigning an infinite penalty to such a cell the activity will be automatically excluded from the optimal solution. Then apply the usual procedure to find the optimal assignment.

Academia.edu no longer supports Internet Explorer.
To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to upgrade your browser .
Enter the email address you signed up with and we'll email you a reset link.
- We're Hiring!
- Help Center

The Quadratic Assignment Problem

Related Papers
Encyclopedia of Optimization
Panos Pardalos
Panos M Pardalos
Abstract This paper aims at describing the state of the art on quadratic assignment problems (QAPs). It discusses the most important developments in all aspects of the QAP such as linearizations, QAP polyhedra, algorithms to solve the problem to optimality, heuristics, polynomially solvable special cases, and asymptotic behavior.
Güneş Erdoğan
The Quadratic Assignment Problem (QAP) is one of the hardest combinatorial optimization problems known. Exact solution attempts proposed for instances of size larger than 15 have been generally unsuccessful even though successful implementations have been reported on some test problems from the QAPLIB up to size 36. In this dissertation, we analyze the binary structure of the QAP and present new IP formulations. We focus on “flow-based” formulations, strengthen the formulations with valid inequalities, and report computational experience with a branch-and-cut algorithm. Next, we present new classes of instances of the QAP that can be completely or partially reduced to the Linear Assignment Problem and give procedures to check whether or not an instance is an element of one of these classes. We also identify classes of instances of the Koopmans-Beckmann form of the QAP that are solvable in polynomial time. Lastly, we present a strong lower bound based on Bender’s decomposition.
Cesar Beltran-Royo
Pesquisa Operacional
Paulo Boaventura Netto
We investigate the classical Gilmore-Lawler lower bound for the quadratic assignment problem. We provide evidence of the difficulty of improving the Gilmore-Lawler bound and develop new bounds by means of optimal reduction schemes. Computational results are reported indicating that the new lower bounds have advantages over previous bounds and can be used in a branch-and-bound type algorithm for the quadratic assignment problem.
Computers & Operations Research
Ricardo P M Ferreira
Ilyes Beltaef
Loading Preview
Sorry, preview is currently unavailable. You can download the paper by clicking the button above.
RELATED PAPERS
Paulo Gonçalves
Dennis Heffley
Franz Rendl
Vittorio Maniezzo
New ideas in optimization
Marco Dorigo
Álvaro M. Valdebenito B.
Journal of Combinatorial Optimization
Madalina Drugan
Ali Safari Mamaghani
Informs Journal on Computing
Dushyant Sharma
Mathematics of Operations Research
Discrete Applied Mathematics
catherine roucairol
IEEE Transactions on Knowledge and Data Engineering
Cut Latifah
European Journal of Operational Research
Bernard Mans
Teodor Crainic
Applied Mathematical Sciences
Hassan Mishmast Nehi
Panos M Pardalos , John Mitchell
Paulo Boaventura-Netto
Ajay Bidyarthy
Yugoslav Journal of …
Journal of Industrial Engineering International
Hossein Karimi
NURDIYANA JAMIL
Ajith Abraham
IEEE Transactions on Information Theory
David Malah
Tansel Dökeroğlu
Matteo Fischetti
Sunderesh Heragu
RELATED TOPICS
- We're Hiring!
- Help Center
- Find new research papers in:
- Health Sciences
- Earth Sciences
- Cognitive Science
- Mathematics
- Computer Science
- Academia ©2024
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Formulation of Assignment problem as integer programming
We need to maintain as quickly as possible a complex system. In particular, we need to replace six of its components $\{P_1,\ldots,P_6\}$ . We have three 3D printers $\{M_1,M_2,M_3\}$ which we can use to fabricate the six components. The following table/matrix states how long it takes (in minutes) the $i$ th printer to print the $j$ th component:
\begin{array}{ccccccc} \hline & P_1& P_2&P_3&P_4&P_5&P_6 \\ \hline M_1 & 23 & 42 & 12 & 32 & 47 & 60\\ M_2 & 25& 37& 13& 37& 51& 64\\ M_3 & 27 &51 &15& 41 &57 &55\\ \hline \end{array}
The complex system will work again only when all the components have been printed. Clearly more components can (and have to be) assigned to single machines and they are made in a sequence, one after the other, and 3D printers can work in parallel. However, you have only two operators and therefore you can only use two machines. How to formulate the problem as a linear (but combinatorial) optimization problem to allocate components to (two out of three) 3D printers so that the maintenance time is minimized.
So far I have tried the following, but I am not quite sure (Please I need help if I was mistaken):
Let $x_{ij}= 1$ if machine $i$ is assigned to component $j$ , $0$ otherwise. The model is \begin{align}\min&\quad23x_{11}+42x_{12}+...+55x_{36}\\\text{s.t.}&\quad x_{11}+x_{12}+x_{13}+x_{14}+x_{15}+x_{16} = 2\\&\quad x_{21}+x_{22}+x_{23}+x_{24}+x_{25}+x_{26} = 2\\&\quad x_{31}+x_{32}+x_{33}+x_{34}+x_{35}+x_{36} = 2\\&\quad x_{11}+x_{21}+x_{31} \ge 1\\&\quad x_{12}+x_{22}+x_{32} \ge 1\\&\quad x_{13}+x_{23}+x_{33} \ge 1\\&\quad x_{14}+x_{24}+x_{34} \ge 1\\&\quad x_{15}+x_{25}+x_{35} \ge 1\\&\quad x_{16}+x_{26}+x_{36} \ge 1\\&\quad x_{ij}\,\,\text{is binary}.\end{align}
- integer-programming
- combinatorial-optimization
- 1 $\begingroup$ "The complex system will work again only when all the components have been printed." Does that mean you'd like the system to end as soon as possible? (Thinking of the objective function here). Besides this, I think this could better be formulated as a scheduling problem on parallel machines, with the additional constraint that only 2 of the 3 machines are used. $\endgroup$ – dhasson Commented Jul 2, 2020 at 13:37
- $\begingroup$ The Generalized Assignment Problem can serve as inspiration to continue, it's the same you are doing but change the first 3 constraints where every machine is made to print 2 components. First of all, the objective function is total working time of the machines. Instead you want to minimize the makespan (maximum time to finish all jobs), so that system can work again as soon as possible. Second, you may add binary variables $z_i = 1$ if machine $i$ is used, with additional constraints for $\sum_i z_i = 2$ and linking $x$ and $z$. $\endgroup$ – dhasson Commented Jul 2, 2020 at 15:30
- 1 $\begingroup$ Are you assuming that one machine will never be used, or that operators will move among machines such that all machines might be used at some point, but never more than two running at any given time? $\endgroup$ – prubin ♦ Commented Jul 2, 2020 at 15:57
- $\begingroup$ @user3752, as dhasson mentioned, it sounds like a parallel machine scheduling problem. Would you see this link? $\endgroup$ – A.Omidi Commented Jul 3, 2020 at 10:41
Since you mention that you want to operate two out of three machines, it boils down to a problem where you first pick two machines and then perform a standard $R2||C_{\max}$ parallel machine scheduling problem with the two machines that you selected. Such problems are very suitable for dynamic programming/column generation approaches, but your instance is so small that a IP will work fine. And since you ask for an IP, let us consider a straightforward way to model it.
For a formulation, consider the following decision variables: $$y_j = \left\{ \begin{array}{ll} 1 & \mbox{ if } M_j \mbox{ is being operated } \\ 0 & \mbox{otherwise} \end{array} \right.$$ and $$x_{ij} = \left\{ \begin{array}{ll} 1 & \mbox{ if } P_i \mbox{ is made on } M_j \\ 0 & \mbox{otherwise} \end{array}\right.$$ Also, let's assume that $a_{ij}$ is the time needed to produce $P_i$ on $M_j$ .
Now the following IP can be formulated: $$\begin{array}{llll} \min & z \\ \mbox{s.t.} & \sum_{j} y_j & \leq K \\ & \sum_{j} x_{ij} & = 1 & \forall i \\ & x_{ij} & \leq y_j & \forall i \forall j \\ & \sum_i a_{ij} x_{ij} & \leq z & \forall j \\ & x_{ij} \in \{0,1\} & & \forall i \forall j \\ & y_j \in \{0,1\} & & \forall j \\ & z \in \mathbb{R} \end{array}$$ Where the objective variable $z$ represents the makespan, the first constraint states that at most $K$ machines can be used (in your instance, $K=2$ , i.e. $K$ is the number of operators), the second constraint states that each $P_i$ must be executed on exactly one $M_j$ , the third constraint states that a $P_i$ can only be produced on a $M_j$ if that $M_j$ is being operated and the fourth constraint states that the makespan $z$ should be at least the time spent on each individual machine.
If you want to allow operators to switch between machines, the problem becomes more complicated, as you need to make sure that both an operator and a machine is available when you produce an item; you probably need to keep track of both the operator and the machine resources in your model and define constraints to avoid conflicts for which you may or may not need to determine an order as well.
Your Answer
Sign up or log in, post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Not the answer you're looking for? Browse other questions tagged integer-programming combinatorial-optimization or ask your own question .
- Featured on Meta
- Upcoming initiatives on Stack Overflow and across the Stack Exchange network...
- We spent a sprint addressing your requests — here’s how it went
Hot Network Questions
- Sum of the vectors to each of the vertices of the polygon
- Type inference with type classes in Coq
- Sort Number Array
- How shall I find the device of a phone's storage so that I can mount it in Linux?
- confidence intervals for proportions containing a theoretically impossible value (zero)
- As an advisor, how can I help students with time management and procrastination?
- How to determine relative contribution of explanatory variables in a linear regression
- Is there a name for the likelihood of the most likely outcome?
- What spells can I cast while swallowed?
- What effects could cause a laser beam inside a pipe to bend?
- How fast does the number of "fixed" points grow compared to the size of the ball in the following group?
- Plane to train in Copenhagen
- Sci-fi book series about a teenage detective, possibly named Diamond, with a floating AI assistant
- How to read chainline specs for crankset and bottom bracket compatibility?
- Who first promoted the idea that the primary purpose of government is to protect its citizens?
- Transparent Glass Material Eevee Blender version 4.2
- How much damage does my Hexblade Warlock deal with their Bonus Action attack?
- TWR of near-term NTR engines
- When Canadian citizen residing abroad comes to visit Canada
- Path integral at large time
- Can you be charged with breaking and entering if the door was open, and the owner of the property is deceased?
- Did any attendees write up accounts of pre-1980 Homebrew Computer Club meetings?
- What is meant by "I was blue ribbon" and "I broke my blue ribbon"?
- Hourly pay rate calculation between Recruiting and Payroll Systems
- Analysis of Algorithms
- Backtracking
- Dynamic Programming
- Divide and Conquer
- Geometric Algorithms
- Mathematical Algorithms
- Pattern Searching
- Bitwise Algorithms
- Branch & Bound
- Randomized Algorithms
Quadratic Assignment Problem (QAP)
The Quadratic Assignment Problem (QAP) is an optimization problem that deals with assigning a set of facilities to a set of locations, considering the pairwise distances and flows between them.
The problem is to find the assignment that minimizes the total cost or distance, taking into account both the distances and the flows.
The distance matrix and flow matrix, as well as restrictions to ensure each facility is assigned to exactly one location and each location is assigned to exactly one facility, can be used to formulate the QAP as a quadratic objective function.
The QAP is a well-known example of an NP-hard problem , which means that for larger cases, computing the best solution might be difficult. As a result, many algorithms and heuristics have been created to quickly identify approximations of answers.
There are various types of algorithms for different problem structures, such as:
- Precise algorithms
- Approximation algorithms
- Metaheuristics like genetic algorithms and simulated annealing
- Specialized algorithms
Example: Given four facilities (F1, F2, F3, F4) and four locations (L1, L2, L3, L4). We have a cost matrix that represents the pairwise distances or costs between facilities. Additionally, we have a flow matrix that represents the interaction or flow between locations. Find the assignment that minimizes the total cost based on the interactions between facilities and locations. Each facility must be assigned to exactly one location, and each location can only accommodate one facility.
Facilities cost matrix:
| L1 | L2 | L3 | L4 | |
|---|---|---|---|---|
| F1 | 0 | 2 | 3 | 1 |
| F2 | 2 | 0 | 1 | 4 |
| F3 | 3 | 1 | 0 | 2 |
| F4 | 1 | 4 | 2 | 0 |
Flow matrix:
| F1 | F2 | F3 | F4 | |
|---|---|---|---|---|
| L1 | 0 | 1 | 2 | 3 |
| L2 | 1 | 0 | 4 | 2 |
| L3 | 2 | 4 | 0 | 1 |
| L4 | 3 | 2 | 1 | 0 |
To solve the QAP, various optimization techniques can be used, such as mathematical programming, heuristics, or metaheuristics. These techniques aim to explore the search space and find the optimal or near-optimal solution.
The solution to the QAP will provide an assignment of facilities to locations that minimizes the overall cost.
The solution generates all possible permutations of the assignment and calculates the total cost for each assignment. The optimal assignment is the one that results in the minimum total cost.
To calculate the total cost, we look at each pair of facilities in (i, j) and their respective locations (location1, location2). We then multiply the cost of assigning facility1 to facility2 (facilities[facility1][facility2]) with the flow from location1 to location2 (locations[location1][location2]). This process is done for all pairs of facilities in the assignment, and the costs are summed up.
Overall, the output tells us that assigning facilities to locations as F1->L1, F3->L2, F2->L3, and F4->L4 results in the minimum total cost of 44. This means that Facility 1 is assigned to Location 1, Facility 3 is assigned to Location 2, Facility 2 is assigned to Location 3, and Facility 4 is assigned to Location 4, yielding the lowest cost based on the given cost and flow matrices.This example demonstrates the process of finding the optimal assignment by considering the costs and flows associated with each facility and location. The objective is to find the assignment that minimizes the total cost, taking into account the interactions between facilities and locations.
Applications of the QAP include facility location, logistics, scheduling, and network architecture, all of which require effective resource allocation and arrangement.
Please Login to comment...
Similar reads, improve your coding skills with practice.
What kind of Experience do you want to share?
- DOI: 10.46254/an14.20240106
- Corpus ID: 270317124
A Revised Formulation for the Airline Fleet Assignment Problem
- Alaa Ahmed , Bassant Nabil , +1 author Ahmad E. Elhabashy
- Published in Proceedings of the… 12 February 2024
- Engineering, Business
Related Papers
Showing 1 through 3 of 0 Related Papers

- Advanced Search
A comparative study of alternative formulations for the periodic vehicle routing problem
New citation alert added.
This alert has been successfully added and will be sent to:
You will be notified whenever a record that you have chosen has been cited.
To manage your alert preferences, click on the button below.
New Citation Alert!
Please log in to your account
Information & Contributors
Bibliometrics & citations, view options, recommendations, a set-covering based heuristic algorithm for the periodic vehicle routing problem.
We present a hybrid optimization algorithm for mixed-integer linear programming, embedding both heuristic and exact components. In order to validate it we use the periodic vehicle routing problem (PVRP) as a case study. This problem consists of ...
Formulations and relaxations for a multi-echelon capacitated location-distribution problem
We consider a multi-echelon location-distribution problem arising from an actual application in fast delivery service. We present and compare two formulations for this problem: an arc-based model and a path-based model. We show that the linear ...
Tight formulations for some simple mixed integer programs and convex objective integer programs
We study the polyhedral structure of simple mixed integer sets that generalize the two variable set {(s,z)źR1+ ź1:sźzźb}. These sets form basic building blocks that can be used to derive tight formulations for more complicated mixed integer programs. ...
Information
Published in.
Elsevier Science Ltd.
United Kingdom
Publication History
Author tags.
- Periodic vehicle routing
- Formulations
- Time windows
- Valid inequalities
- Benchmark instances
- Research-article
Contributors
Other metrics, bibliometrics, article metrics.
- 0 Total Citations
- 0 Total Downloads
- Downloads (Last 12 months) 0
- Downloads (Last 6 weeks) 0
View options
Login options.
Check if you have access through your login credentials or your institution to get full access on this article.
Full Access
Share this publication link.
Copying failed.
Share on social media
Affiliations, export citations.
- Please download or close your previous search result export first before starting a new bulk export. Preview is not available. By clicking download, a status dialog will open to start the export process. The process may take a few minutes but once it finishes a file will be downloadable from your browser. You may continue to browse the DL while the export process is in progress. Download
- Download citation
- Copy citation
We are preparing your search results for download ...
We will inform you here when the file is ready.
Your file of search results citations is now ready.
Your search export query has expired. Please try again.

IMAGES
VIDEO
COMMENTS
The assignment problem is a fundamental combinatorial optimization problem. In its most general form, the problem is as follows: ... While this formulation allows also fractional variable values, in this special case, the LP always has an optimal solution where the variables take integer values.
Definition and formulation. Consider the problem of assigning n jobs to n machines (one job to one machine). Let Cij be the cost of assigning ith job to the jth machine and xij represents the assignment of ith job to the jth machine. xij is missing in any cell means that no assignment is made between the pair of job and machine. (i.e) xij = 0.
After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations. Meaning of Assignment Problem: An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total ...
In an assignment problem, we must find a maximum matching that has the minimum weight in a weighted bipartite graph. The Assignment problem. Problem description: 3 men apply for 3 jobs. Each applicant gets one job. The suitability of each candidate for each job is represented by a cost: The lower the cost ...
This lecture discusses the assignment problemsOther videos @DrHarishGarg Assignment Problem - Mathematical Models: Link: https://youtu.be/OX1ssZez_sYHungaria...
The assignment problem arises when $ m = n $ and all $ a _ {i} $ and $ b _ {j} $ are $ 1 $. If all $ a _ {i} $ and $ b _ {j} $ in the transposed problem are integers, then there is an optimal solution for which all $ x _ {ij } $ are integers (Dantzig's theorem on integral solutions of the transport problem). In the assignment problem, for such ...
8.1 Introduction. An assignment problem is a particular case of transportation problem in which a number of operations are to be assigned to an equal number of operators, where each operator performs only one operation. The objective is to minimize overall cost or to maximize the overall profit for a given assignment schedule.
The Koopmans-Beckman formulation of the QAP aims to achieve the objective of assigning facilities to locations in order to minimize the overall cost. Below is the Koopmans-Beckman formulation of the QAP as described by neos-guide.org. Quadratic Assignment Problem Formulation Parameters
In general, an assignment problem is a balanced trans- portation problem in which all supplies and demands are equal to 1. Thus, an assignment problem is characterized by knowledge of the cost of assigning each supply point to each demand point. The assignment problem k matrix of costs is its cost matrix. Ignoring for the moment the = 0 or = 1 ...
8.3 Mathematical Formulation of Assignment Problem . Using the notations described above, the assignment problem consist of finding the values of X ij in order to minimize the total cost Subject to restrictions where X ij denotes the j th job to be assigned to the i th person. An assignment problem could thus be solved by Simplex Method.
Formulation of an assignment problem . Suppose a company has n persons of different capacities available for performing each different job in the concern, and there are the same number of jobs of different types. One person can be given one and only one job. The objective of this assignment problem is to assign n persons to n jobs, so as to ...
1 Formulation of the problem. Suppose that there are [math]n[/math] agents and [math]m[/math] tasks, which can be distributed between these agents. Only one task can be assigned to each agent, and each task can be assigned to only one agent. The cost of assignment of the [math]i[/math]-th task to the [math]j[/math]-th agent is [math]c(i, j)[/math].If [math]c(i, j) = \infty[/math], then the ...
e BiQuadratic Assignment Problemgeneralization of the QAP is the BiQuadratic Assignment Problem, denoted BiQAP, which is essentially a quartic assignment problem with cost coefficients formed by the product. of two four-dimensional arrays. More specifica. ly, consider two n4 × n4. rrays= (fijkl) and D = (dmpst).
The quadratic assignment problem (QAP) has considered one of the most significant combinatorial optimization problems due to its variant and significant applications in real life such as scheduling, production, computer manufacture, chemistry, facility location, communication, and other fields. QAP is NP-hard problem that is impossible to be solved in polynomial time when the problem size ...
Mathematical Formulation: Any basic feasible solution of an Assignment problem consists (2n - 1) variables of which the (n - 1) variables are zero, n is number of jobs or number of facilities. Due to this high degeneracy, if we solve the problem by usual transportation method, it will be a complex and time consuming work. Thus a separate ...
2.2 Formulation of Assignment Problem[34] The decision problem becomes complicated when a number of resources are required to be allocated and there are several activities to perform. The decision problem can be formulated, and solved, as mathematical programming problem. The Assignment problem can be stated in the form of n x n matrix, [C ...
Biquadratic Assignment Problem. A generalization of the QAP is the biquadratic assignment problem (BiQAP), which is essentially a quartic assignment problem with cost coefficients formed by the products of two four-dimensional arrays. More specifically, consider two n 4 × n 4 arrays F = ( f ijkl ) and D = ( d mpst ).
It may be observed from the above formulation that AP is a special type of Linear programming problem. Unbalanced Assignment Problem. If the cost matrix of an assignment problem is not a square matrix, the assignment problem is called an Unbalanced Assignment Problem. In such a case, add dummy row or dummy column with zero cost in the cost ...
The solution of QAP (F, D) produced by an ǫ-approximation algorithm is called an ǫ-approximate solution. Theorem 3.2 (Sahni and Gonzalez [164], 1976) The quadratic assignment problem is strongly NP-hard. For an arbitrary ǫ > 0, the existence of a polynomial time ǫ-approximation algorithm for the QAP implies P = N P.
$\begingroup$ The Generalized Assignment Problem can serve as inspiration to continue, it's the same you are doing but change the first 3 constraints where every machine is made to print 2 components. First of all, the objective function is total working time of the machines. Instead you want to minimize the makespan (maximum time to finish all jobs), so that system can work again as soon as ...
The Quadratic Assignment Problem (QAP) is an optimization problem that deals with assigning a set of facilities to a set of locations, considering the pairwise distances and flows between them.. The problem is to find the assignment that minimizes the total cost or distance, taking into account both the distances and the flows. The distance matrix and flow matrix, as well as restrictions to ...
Identify the relationship between assignment problems and transportation problems. 8. Formulate a spreadsheet model for an assignment problem from a description of the problem. 9. ... illustrate the formulation of spreadsheet models for such problems, and survey a variety of applications. The subsequent sections then do the same for
A mathematical formulation of assignment problem. The assignment problem is a linear programming problem that entails allocating resources to individual tasks. It does so that the process's cost or time is kept to a minimum while the profit or sale is maximised. Though similar problems can be handled using simplex or transportation methods ...
DOI: 10.46254/an14.20240106 Corpus ID: 270317124; A Revised Formulation for the Airline Fleet Assignment Problem @article{Ahmed2024ARF, title={A Revised Formulation for the Airline Fleet Assignment Problem}, author={Alaa Ahmed and Bassant Nabil and Hadi Fors and Ahmad E. Elhabashy}, journal={Proceedings of the International Conference on Industrial Engineering and Operations Management}, year ...
This study investigates the periodic vehicle routing problem (PVRP) and its variant with time windows with a particular focus on alternative formulation approaches that can be solved by a state-of-the-art commercial solver. We propose a new vehicle flow formulation for the PVRP and strengthen it with valid inequalities.