Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base

An Introduction to t Tests | Definitions, Formula and Examples
Published on January 31, 2020 by Rebecca Bevans . Revised on June 22, 2023.
A t test is a statistical test that is used to compare the means of two groups. It is often used in hypothesis testing to determine whether a process or treatment actually has an effect on the population of interest, or whether two groups are different from one another.
- The null hypothesis ( H 0 ) is that the true difference between these group means is zero.
- The alternate hypothesis ( H a ) is that the true difference is different from zero.
Table of contents
When to use a t test, what type of t test should i use, performing a t test, interpreting test results, presenting the results of a t test, other interesting articles, frequently asked questions about t tests.
A t test can only be used when comparing the means of two groups (a.k.a. pairwise comparison). If you want to compare more than two groups, or if you want to do multiple pairwise comparisons, use an ANOVA test or a post-hoc test.
The t test is a parametric test of difference, meaning that it makes the same assumptions about your data as other parametric tests. The t test assumes your data:
- are independent
- are (approximately) normally distributed
- have a similar amount of variance within each group being compared (a.k.a. homogeneity of variance)
If your data do not fit these assumptions, you can try a nonparametric alternative to the t test, such as the Wilcoxon Signed-Rank test for data with unequal variances .
Here's why students love Scribbr's proofreading services
Discover proofreading & editing
When choosing a t test, you will need to consider two things: whether the groups being compared come from a single population or two different populations, and whether you want to test the difference in a specific direction.

One-sample, two-sample, or paired t test?
- If the groups come from a single population (e.g., measuring before and after an experimental treatment), perform a paired t test . This is a within-subjects design .
- If the groups come from two different populations (e.g., two different species, or people from two separate cities), perform a two-sample t test (a.k.a. independent t test ). This is a between-subjects design .
- If there is one group being compared against a standard value (e.g., comparing the acidity of a liquid to a neutral pH of 7), perform a one-sample t test .
One-tailed or two-tailed t test?
- If you only care whether the two populations are different from one another, perform a two-tailed t test .
- If you want to know whether one population mean is greater than or less than the other, perform a one-tailed t test.
- Your observations come from two separate populations (separate species), so you perform a two-sample t test.
- You don’t care about the direction of the difference, only whether there is a difference, so you choose to use a two-tailed t test.
The t test estimates the true difference between two group means using the ratio of the difference in group means over the pooled standard error of both groups. You can calculate it manually using a formula, or use statistical analysis software.
T test formula
The formula for the two-sample t test (a.k.a. the Student’s t-test) is shown below.
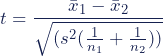
In this formula, t is the t value, x 1 and x 2 are the means of the two groups being compared, s 2 is the pooled standard error of the two groups, and n 1 and n 2 are the number of observations in each of the groups.
A larger t value shows that the difference between group means is greater than the pooled standard error, indicating a more significant difference between the groups.
You can compare your calculated t value against the values in a critical value chart (e.g., Student’s t table) to determine whether your t value is greater than what would be expected by chance. If so, you can reject the null hypothesis and conclude that the two groups are in fact different.
T test function in statistical software
Most statistical software (R, SPSS, etc.) includes a t test function. This built-in function will take your raw data and calculate the t value. It will then compare it to the critical value, and calculate a p -value . This way you can quickly see whether your groups are statistically different.
In your comparison of flower petal lengths, you decide to perform your t test using R. The code looks like this:
Download the data set to practice by yourself.
Sample data set
If you perform the t test for your flower hypothesis in R, you will receive the following output:

The output provides:
- An explanation of what is being compared, called data in the output table.
- The t value : -33.719. Note that it’s negative; this is fine! In most cases, we only care about the absolute value of the difference, or the distance from 0. It doesn’t matter which direction.
- The degrees of freedom : 30.196. Degrees of freedom is related to your sample size, and shows how many ‘free’ data points are available in your test for making comparisons. The greater the degrees of freedom, the better your statistical test will work.
- The p value : 2.2e-16 (i.e. 2.2 with 15 zeros in front). This describes the probability that you would see a t value as large as this one by chance.
- A statement of the alternative hypothesis ( H a ). In this test, the H a is that the difference is not 0.
- The 95% confidence interval . This is the range of numbers within which the true difference in means will be 95% of the time. This can be changed from 95% if you want a larger or smaller interval, but 95% is very commonly used.
- The mean petal length for each group.
Receive feedback on language, structure, and formatting
Professional editors proofread and edit your paper by focusing on:
- Academic style
- Vague sentences
- Style consistency
See an example
When reporting your t test results, the most important values to include are the t value , the p value , and the degrees of freedom for the test. These will communicate to your audience whether the difference between the two groups is statistically significant (a.k.a. that it is unlikely to have happened by chance).
You can also include the summary statistics for the groups being compared, namely the mean and standard deviation . In R, the code for calculating the mean and the standard deviation from the data looks like this:
flower.data %>% group_by(Species) %>% summarize(mean_length = mean(Petal.Length), sd_length = sd(Petal.Length))
In our example, you would report the results like this:
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Chi square test of independence
- Statistical power
- Descriptive statistics
- Degrees of freedom
- Pearson correlation
- Null hypothesis
Methodology
- Double-blind study
- Case-control study
- Research ethics
- Data collection
- Hypothesis testing
- Structured interviews
Research bias
- Hawthorne effect
- Unconscious bias
- Recall bias
- Halo effect
- Self-serving bias
- Information bias
A t-test is a statistical test that compares the means of two samples . It is used in hypothesis testing , with a null hypothesis that the difference in group means is zero and an alternate hypothesis that the difference in group means is different from zero.
A t-test measures the difference in group means divided by the pooled standard error of the two group means.
In this way, it calculates a number (the t-value) illustrating the magnitude of the difference between the two group means being compared, and estimates the likelihood that this difference exists purely by chance (p-value).
Your choice of t-test depends on whether you are studying one group or two groups, and whether you care about the direction of the difference in group means.
If you are studying one group, use a paired t-test to compare the group mean over time or after an intervention, or use a one-sample t-test to compare the group mean to a standard value. If you are studying two groups, use a two-sample t-test .
If you want to know only whether a difference exists, use a two-tailed test . If you want to know if one group mean is greater or less than the other, use a left-tailed or right-tailed one-tailed test .
A one-sample t-test is used to compare a single population to a standard value (for example, to determine whether the average lifespan of a specific town is different from the country average).
A paired t-test is used to compare a single population before and after some experimental intervention or at two different points in time (for example, measuring student performance on a test before and after being taught the material).
A t-test should not be used to measure differences among more than two groups, because the error structure for a t-test will underestimate the actual error when many groups are being compared.
If you want to compare the means of several groups at once, it’s best to use another statistical test such as ANOVA or a post-hoc test.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bevans, R. (2023, June 22). An Introduction to t Tests | Definitions, Formula and Examples. Scribbr. Retrieved July 1, 2024, from https://www.scribbr.com/statistics/t-test/
Is this article helpful?
Rebecca Bevans
Other students also liked, choosing the right statistical test | types & examples, hypothesis testing | a step-by-step guide with easy examples, test statistics | definition, interpretation, and examples, what is your plagiarism score.
Two Sample t-test: Definition, Formula, and Example
A two sample t-test is used to determine whether or not two population means are equal.
This tutorial explains the following:
- The motivation for performing a two sample t-test.
- The formula to perform a two sample t-test.
- The assumptions that should be met to perform a two sample t-test.
- An example of how to perform a two sample t-test.
Two Sample t-test: Motivation
Suppose we want to know whether or not the mean weight between two different species of turtles is equal. Since there are thousands of turtles in each population, it would be too time-consuming and costly to go around and weigh each individual turtle.
Instead, we might take a simple random sample of 15 turtles from each population and use the mean weight in each sample to determine if the mean weight is equal between the two populations:

However, it’s virtually guaranteed that the mean weight between the two samples will be at least a little different. The question is whether or not this difference is statistically significant . Fortunately, a two sample t-test allows us to answer this question.
Two Sample t-test: Formula
A two-sample t-test always uses the following null hypothesis:
- H 0 : μ 1 = μ 2 (the two population means are equal)
The alternative hypothesis can be either two-tailed, left-tailed, or right-tailed:
- H 1 (two-tailed): μ 1 ≠ μ 2 (the two population means are not equal)
- H 1 (left-tailed): μ 1 2 (population 1 mean is less than population 2 mean)
- H 1 (right-tailed): μ 1 > μ 2 (population 1 mean is greater than population 2 mean)
We use the following formula to calculate the test statistic t:
Test statistic: ( x 1 – x 2 ) / s p (√ 1/n 1 + 1/n 2 )
where x 1 and x 2 are the sample means, n 1 and n 2 are the sample sizes, and where s p is calculated as:
s p = √ (n 1 -1)s 1 2 + (n 2 -1)s 2 2 / (n 1 +n 2 -2)
where s 1 2 and s 2 2 are the sample variances.
If the p-value that corresponds to the test statistic t with (n 1 +n 2 -1) degrees of freedom is less than your chosen significance level (common choices are 0.10, 0.05, and 0.01) then you can reject the null hypothesis.
Two Sample t-test: Assumptions
For the results of a two sample t-test to be valid, the following assumptions should be met:
- The observations in one sample should be independent of the observations in the other sample.
- The data should be approximately normally distributed.
- The two samples should have approximately the same variance. If this assumption is not met, you should instead perform Welch’s t-test .
- The data in both samples was obtained using a random sampling method .
Two Sample t-test : Example
Suppose we want to know whether or not the mean weight between two different species of turtles is equal. To test this, will perform a two sample t-test at significance level α = 0.05 using the following steps:
Step 1: Gather the sample data.
Suppose we collect a random sample of turtles from each population with the following information:
- Sample size n 1 = 40
- Sample mean weight x 1 = 300
- Sample standard deviation s 1 = 18.5
- Sample size n 2 = 38
- Sample mean weight x 2 = 305
- Sample standard deviation s 2 = 16.7
Step 2: Define the hypotheses.
We will perform the two sample t-test with the following hypotheses:
- H 0 : μ 1 = μ 2 (the two population means are equal)
- H 1 : μ 1 ≠ μ 2 (the two population means are not equal)
Step 3: Calculate the test statistic t .
First, we will calculate the pooled standard deviation s p :
s p = √ (n 1 -1)s 1 2 + (n 2 -1)s 2 2 / (n 1 +n 2 -2) = √ (40-1)18.5 2 + (38-1)16.7 2 / (40+38-2) = 17.647
Next, we will calculate the test statistic t :
t = ( x 1 – x 2 ) / s p (√ 1/n 1 + 1/n 2 ) = (300-305) / 17.647(√ 1/40 + 1/38 ) = -1.2508
Step 4: Calculate the p-value of the test statistic t .
According to the T Score to P Value Calculator , the p-value associated with t = -1.2508 and degrees of freedom = n 1 +n 2 -2 = 40+38-2 = 76 is 0.21484 .
Step 5: Draw a conclusion.
Since this p-value is not less than our significance level α = 0.05, we fail to reject the null hypothesis. We do not have sufficient evidence to say that the mean weight of turtles between these two populations is different.
Note: You can also perform this entire two sample t-test by simply using the Two Sample t-test Calculator .
Additional Resources
The following tutorials explain how to perform a two-sample t-test using different statistical programs:
How to Perform a Two Sample t-test in Excel How to Perform a Two Sample t-test in SPSS How to Perform a Two Sample t-test in Stata How to Perform a Two Sample t-test in R How to Perform a Two Sample t-test in Python How to Perform a Two Sample t-test on a TI-84 Calculator
An Introduction to the Binomial Distribution
4 examples of using linear regression in real life, related posts, three-way anova: definition & example, two sample z-test: definition, formula, and example, one sample z-test: definition, formula, and example, how to find a confidence interval for a..., an introduction to the exponential distribution, an introduction to the uniform distribution, the breusch-pagan test: definition & example, population vs. sample: what’s the difference, introduction to multiple linear regression, dunn’s test for multiple comparisons.
JMP | Statistical Discovery.™ From SAS.
Statistics Knowledge Portal
A free online introduction to statistics
The Two-Sample t -Test
What is the two-sample t -test.
The two-sample t -test (also known as the independent samples t -test) is a method used to test whether the unknown population means of two groups are equal or not.
Is this the same as an A/B test?
Yes, a two-sample t -test is used to analyze the results from A/B tests.
When can I use the test?
You can use the test when your data values are independent, are randomly sampled from two normal populations and the two independent groups have equal variances.
What if I have more than two groups?
Use a multiple comparison method. Analysis of variance (ANOVA) is one such method. Other multiple comparison methods include the Tukey-Kramer test of all pairwise differences, analysis of means (ANOM) to compare group means to the overall mean or Dunnett’s test to compare each group mean to a control mean.
What if the variances for my two groups are not equal?
You can still use the two-sample t- test. You use a different estimate of the standard deviation.
What if my data isn’t nearly normally distributed?
If your sample sizes are very small, you might not be able to test for normality. You might need to rely on your understanding of the data. When you cannot safely assume normality, you can perform a nonparametric test that doesn’t assume normality.
See how to perform a two-sample t -test using statistical software
- Download JMP to follow along using the sample data included with the software.
- To see more JMP tutorials, visit the JMP Learning Library .
Using the two-sample t -test
The sections below discuss what is needed to perform the test, checking our data, how to perform the test and statistical details.
What do we need?
For the two-sample t -test, we need two variables. One variable defines the two groups. The second variable is the measurement of interest.
We also have an idea, or hypothesis, that the means of the underlying populations for the two groups are different. Here are a couple of examples:
- We have students who speak English as their first language and students who do not. All students take a reading test. Our two groups are the native English speakers and the non-native speakers. Our measurements are the test scores. Our idea is that the mean test scores for the underlying populations of native and non-native English speakers are not the same. We want to know if the mean score for the population of native English speakers is different from the people who learned English as a second language.
- We measure the grams of protein in two different brands of energy bars. Our two groups are the two brands. Our measurement is the grams of protein for each energy bar. Our idea is that the mean grams of protein for the underlying populations for the two brands may be different. We want to know if we have evidence that the mean grams of protein for the two brands of energy bars is different or not.
Two-sample t -test assumptions
To conduct a valid test:
- Data values must be independent. Measurements for one observation do not affect measurements for any other observation.
- Data in each group must be obtained via a random sample from the population.
- Data in each group are normally distributed .
- Data values are continuous.
- The variances for the two independent groups are equal.
For very small groups of data, it can be hard to test these requirements. Below, we'll discuss how to check the requirements using software and what to do when a requirement isn’t met.
Two-sample t -test example
One way to measure a person’s fitness is to measure their body fat percentage. Average body fat percentages vary by age, but according to some guidelines, the normal range for men is 15-20% body fat, and the normal range for women is 20-25% body fat.
Our sample data is from a group of men and women who did workouts at a gym three times a week for a year. Then, their trainer measured the body fat. The table below shows the data.
Table 1: Body fat percentage data grouped by gender
| Group | Body Fat Percentages | ||||
Men | 13.3 | 6.0 | 20.0 | 8.0 | 14.0 |
| 19.0 | 18.0 | 25.0 | 16.0 | 24.0 | |
| 15.0 | 1.0 | 15.0 | |||
Women | 22.0 | 16.0 | 21.7 | 21.0 | 30.0 |
| 26.0 | 12.0 | 23.2 | 28.0 | 23.0 | |
You can clearly see some overlap in the body fat measurements for the men and women in our sample, but also some differences. Just by looking at the data, it's hard to draw any solid conclusions about whether the underlying populations of men and women at the gym have the same mean body fat. That is the value of statistical tests – they provide a common, statistically valid way to make decisions, so that everyone makes the same decision on the same set of data values.
Checking the data
Let’s start by answering: Is the two-sample t -test an appropriate method to evaluate the difference in body fat between men and women?
- The data values are independent. The body fat for any one person does not depend on the body fat for another person.
- We assume the people measured represent a simple random sample from the population of members of the gym.
- We assume the data are normally distributed, and we can check this assumption.
- The data values are body fat measurements. The measurements are continuous.
- We assume the variances for men and women are equal, and we can check this assumption.
Before jumping into analysis, we should always take a quick look at the data. The figure below shows histograms and summary statistics for the men and women.
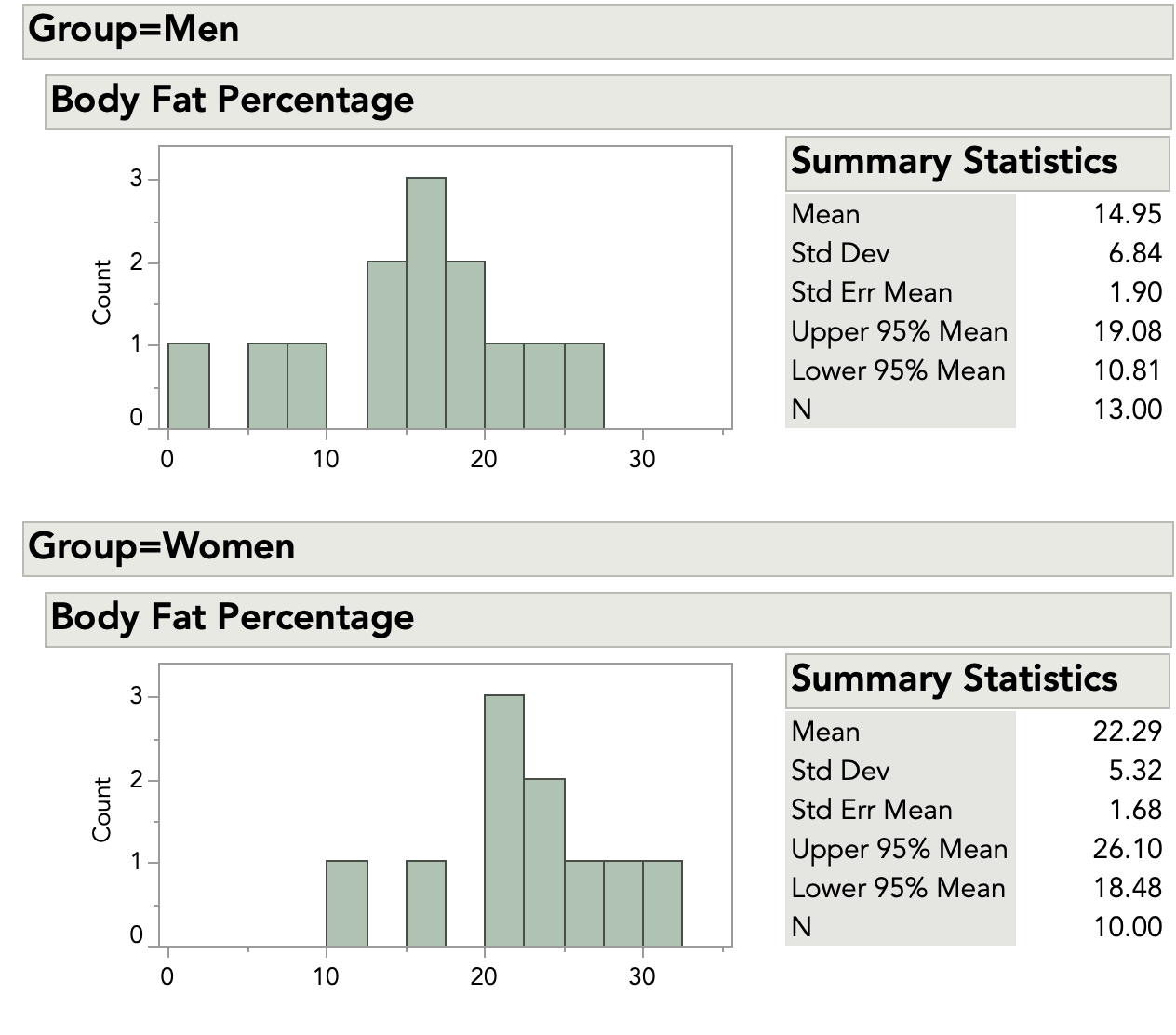
The two histograms are on the same scale. From a quick look, we can see that there are no very unusual points, or outliers . The data look roughly bell-shaped, so our initial idea of a normal distribution seems reasonable.
Examining the summary statistics, we see that the standard deviations are similar. This supports the idea of equal variances. We can also check this using a test for variances.
Based on these observations, the two-sample t -test appears to be an appropriate method to test for a difference in means.

How to perform the two-sample t -test
For each group, we need the average, standard deviation and sample size. These are shown in the table below.
Table 2: Average, standard deviation and sample size statistics grouped by gender
| Women | 10 | 22.29 | 5.32 |
| Men | 13 | 14.95 | 6.84 |
Without doing any testing, we can see that the averages for men and women in our samples are not the same. But how different are they? Are the averages “close enough” for us to conclude that mean body fat is the same for the larger population of men and women at the gym? Or are the averages too different for us to make this conclusion?
We'll further explain the principles underlying the two sample t -test in the statistical details section below, but let's first proceed through the steps from beginning to end. We start by calculating our test statistic. This calculation begins with finding the difference between the two averages:
$ 22.29 - 14.95 = 7.34 $
This difference in our samples estimates the difference between the population means for the two groups.
Next, we calculate the pooled standard deviation. This builds a combined estimate of the overall standard deviation. The estimate adjusts for different group sizes. First, we calculate the pooled variance:
$ s_p^2 = \frac{((n_1 - 1)s_1^2) + ((n_2 - 1)s_2^2)} {n_1 + n_2 - 2} $
$ s_p^2 = \frac{((10 - 1)5.32^2) + ((13 - 1)6.84^2)}{(10 + 13 - 2)} $
$ = \frac{(9\times28.30) + (12\times46.82)}{21} $
$ = \frac{(254.7 + 561.85)}{21} $
$ =\frac{816.55}{21} = 38.88 $
Next, we take the square root of the pooled variance to get the pooled standard deviation. This is:
$ \sqrt{38.88} = 6.24 $
We now have all the pieces for our test statistic. We have the difference of the averages, the pooled standard deviation and the sample sizes. We calculate our test statistic as follows:
$ t = \frac{\text{difference of group averages}}{\text{standard error of difference}} = \frac{7.34}{(6.24\times \sqrt{(1/10 + 1/13)})} = \frac{7.34}{2.62} = 2.80 $
To evaluate the difference between the means in order to make a decision about our gym programs, we compare the test statistic to a theoretical value from the t- distribution. This activity involves four steps:
- We decide on the risk we are willing to take for declaring a significant difference. For the body fat data, we decide that we are willing to take a 5% risk of saying that the unknown population means for men and women are not equal when they really are. In statistics-speak, the significance level, denoted by α, is set to 0.05. It is a good practice to make this decision before collecting the data and before calculating test statistics.
- We calculate a test statistic. Our test statistic is 2.80.
- We find the theoretical value from the t- distribution based on our null hypothesis which states that the means for men and women are equal. Most statistics books have look-up tables for the t- distribution. You can also find tables online. The most likely situation is that you will use software and will not use printed tables. To find this value, we need the significance level (α = 0.05) and the degrees of freedom . The degrees of freedom ( df ) are based on the sample sizes of the two groups. For the body fat data, this is: $ df = n_1 + n_2 - 2 = 10 + 13 - 2 = 21 $ The t value with α = 0.05 and 21 degrees of freedom is 2.080.
- We compare the value of our statistic (2.80) to the t value. Since 2.80 > 2.080, we reject the null hypothesis that the mean body fat for men and women are equal, and conclude that we have evidence body fat in the population is different between men and women.
Statistical details
Let’s look at the body fat data and the two-sample t -test using statistical terms.
Our null hypothesis is that the underlying population means are the same. The null hypothesis is written as:
$ H_o: \mathrm{\mu_1} =\mathrm{\mu_2} $
The alternative hypothesis is that the means are not equal. This is written as:
$ H_o: \mathrm{\mu_1} \neq \mathrm{\mu_2} $
We calculate the average for each group, and then calculate the difference between the two averages. This is written as:
$\overline{x_1} - \overline{x_2} $
We calculate the pooled standard deviation. This assumes that the underlying population variances are equal. The pooled variance formula is written as:
The formula shows the sample size for the first group as n 1 and the second group as n 2 . The standard deviations for the two groups are s 1 and s 2 . This estimate allows the two groups to have different numbers of observations. The pooled standard deviation is the square root of the variance and is written as s p .
What if your sample sizes for the two groups are the same? In this situation, the pooled estimate of variance is simply the average of the variances for the two groups:
$ s_p^2 = \frac{(s_1^2 + s_2^2)}{2} $
The test statistic is calculated as:
$ t = \frac{(\overline{x_1} -\overline{x_2})}{s_p\sqrt{1/n_1 + 1/n_2}} $
The numerator of the test statistic is the difference between the two group averages. It estimates the difference between the two unknown population means. The denominator is an estimate of the standard error of the difference between the two unknown population means.
Technical Detail: For a single mean, the standard error is $ s/\sqrt{n} $ . The formula above extends this idea to two groups that use a pooled estimate for s (standard deviation), and that can have different group sizes.
We then compare the test statistic to a t value with our chosen alpha value and the degrees of freedom for our data. Using the body fat data as an example, we set α = 0.05. The degrees of freedom ( df ) are based on the group sizes and are calculated as:
$ df = n_1 + n_2 - 2 = 10 + 13 - 2 = 21 $
The formula shows the sample size for the first group as n 1 and the second group as n 2 . Statisticians write the t value with α = 0.05 and 21 degrees of freedom as:
$ t_{0.05,21} $
The t value with α = 0.05 and 21 degrees of freedom is 2.080. There are two possible results from our comparison:
- The test statistic is lower than the t value. You fail to reject the hypothesis of equal means. You conclude that the data support the assumption that the men and women have the same average body fat.
- The test statistic is higher than the t value. You reject the hypothesis of equal means. You do not conclude that men and women have the same average body fat.
t -Test with unequal variances
When the variances for the two groups are not equal, we cannot use the pooled estimate of standard deviation. Instead, we take the standard error for each group separately. The test statistic is:
$ t = \frac{ (\overline{x_1} - \overline{x_2})}{\sqrt{s_1^2/n_1 + s_2^2/n_2}} $
The numerator of the test statistic is the same. It is the difference between the averages of the two groups. The denominator is an estimate of the overall standard error of the difference between means. It is based on the separate standard error for each group.
The degrees of freedom calculation for the t value is more complex with unequal variances than equal variances and is usually left up to statistical software packages. The key point to remember is that if you cannot use the pooled estimate of standard deviation, then you cannot use the simple formula for the degrees of freedom.
Testing for normality
The normality assumption is more important when the two groups have small sample sizes than for larger sample sizes.
Normal distributions are symmetric, which means they are “even” on both sides of the center. Normal distributions do not have extreme values, or outliers. You can check these two features of a normal distribution with graphs. Earlier, we decided that the body fat data was “close enough” to normal to go ahead with the assumption of normality. The figure below shows a normal quantile plot for men and women, and supports our decision.
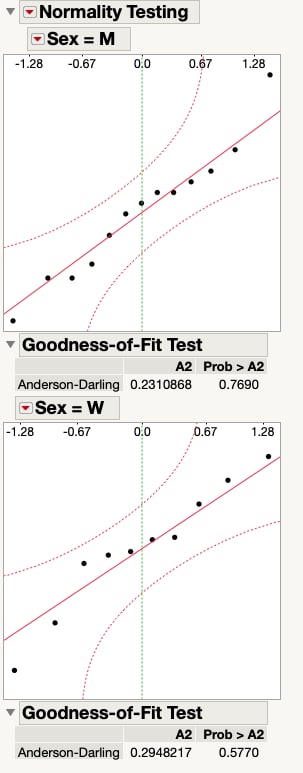
You can also perform a formal test for normality using software. The figure above shows results of testing for normality with JMP software. We test each group separately. Both the test for men and the test for women show that we cannot reject the hypothesis of a normal distribution. We can go ahead with the assumption that the body fat data for men and for women are normally distributed.
Testing for unequal variances
Testing for unequal variances is complex. We won’t show the calculations in detail, but will show the results from JMP software. The figure below shows results of a test for unequal variances for the body fat data.

Without diving into details of the different types of tests for unequal variances, we will use the F test. Before testing, we decide to accept a 10% risk of concluding the variances are equal when they are not. This means we have set α = 0.10.
Like most statistical software, JMP shows the p -value for a test. This is the likelihood of finding a more extreme value for the test statistic than the one observed. It’s difficult to calculate by hand. For the figure above, with the F test statistic of 1.654, the p- value is 0.4561. This is larger than our α value: 0.4561 > 0.10. We fail to reject the hypothesis of equal variances. In practical terms, we can go ahead with the two-sample t -test with the assumption of equal variances for the two groups.
Understanding p-values
Using a visual, you can check to see if your test statistic is a more extreme value in the distribution. The figure below shows a t- distribution with 21 degrees of freedom.
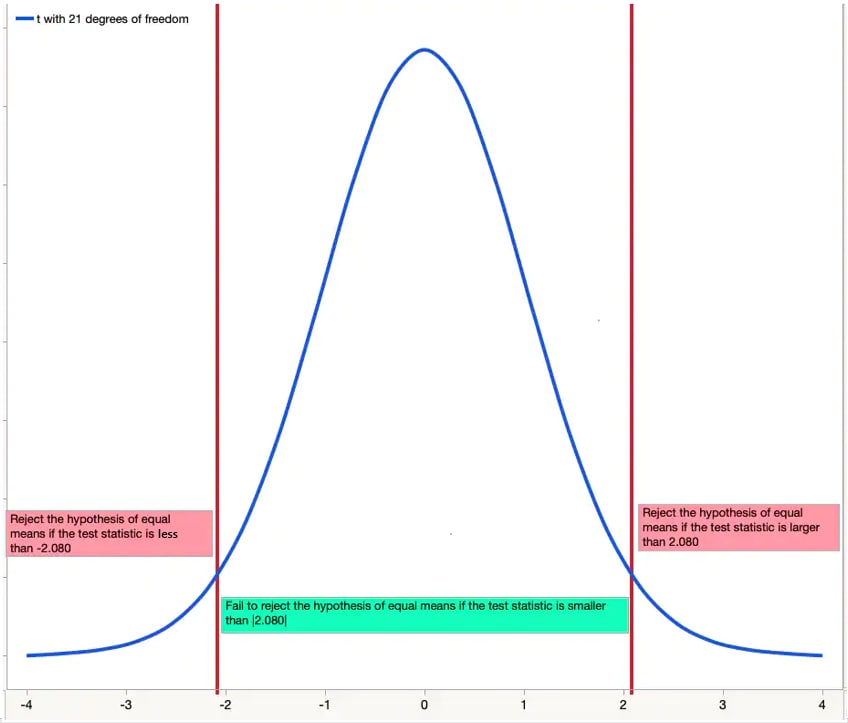
Since our test is two-sided and we have set α = .05, the figure shows that the value of 2.080 “cuts off” 2.5% of the data in each of the two tails. Only 5% of the data overall is further out in the tails than 2.080. Because our test statistic of 2.80 is beyond the cut-off point, we reject the null hypothesis of equal means.
Putting it all together with software
The figure below shows results for the two-sample t -test for the body fat data from JMP software.
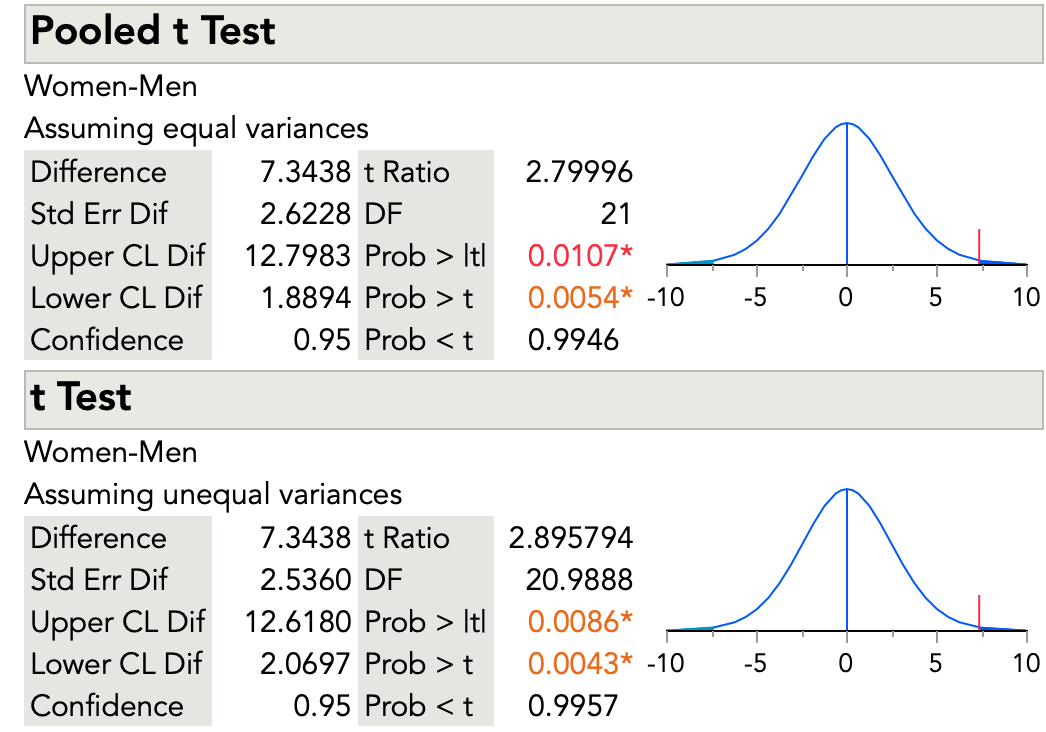
The results for the two-sample t -test that assumes equal variances are the same as our calculations earlier. The test statistic is 2.79996. The software shows results for a two-sided test and for one-sided tests. The two-sided test is what we want (Prob > |t|). Our null hypothesis is that the mean body fat for men and women is equal. Our alternative hypothesis is that the mean body fat is not equal. The one-sided tests are for one-sided alternative hypotheses – for example, for a null hypothesis that mean body fat for men is less than that for women.
We can reject the hypothesis of equal mean body fat for the two groups and conclude that we have evidence body fat differs in the population between men and women. The software shows a p -value of 0.0107. We decided on a 5% risk of concluding the mean body fat for men and women are different, when they are not. It is important to make this decision before doing the statistical test.
The figure also shows the results for the t- test that does not assume equal variances. This test does not use the pooled estimate of the standard deviation. As was mentioned above, this test also has a complex formula for degrees of freedom. You can see that the degrees of freedom are 20.9888. The software shows a p- value of 0.0086. Again, with our decision of a 5% risk, we can reject the null hypothesis of equal mean body fat for men and women.
Other topics
If you have more than two independent groups, you cannot use the two-sample t- test. You should use a multiple comparison method. ANOVA, or analysis of variance, is one such method. Other multiple comparison methods include the Tukey-Kramer test of all pairwise differences, analysis of means (ANOM) to compare group means to the overall mean or Dunnett’s test to compare each group mean to a control mean.
What if my data are not from normal distributions?
If your sample size is very small, it might be hard to test for normality. In this situation, you might need to use your understanding of the measurements. For example, for the body fat data, the trainer knows that the underlying distribution of body fat is normally distributed. Even for a very small sample, the trainer would likely go ahead with the t -test and assume normality.
What if you know the underlying measurements are not normally distributed? Or what if your sample size is large and the test for normality is rejected? In this situation, you can use nonparametric analyses. These types of analyses do not depend on an assumption that the data values are from a specific distribution. For the two-sample t -test, the Wilcoxon rank sum test is a nonparametric test that could be used.
Independent t-test for two samples
Introduction.
The independent t-test, also called the two sample t-test, independent-samples t-test or student's t-test, is an inferential statistical test that determines whether there is a statistically significant difference between the means in two unrelated groups.
Null and alternative hypotheses for the independent t-test
The null hypothesis for the independent t-test is that the population means from the two unrelated groups are equal:
H 0 : u 1 = u 2
In most cases, we are looking to see if we can show that we can reject the null hypothesis and accept the alternative hypothesis, which is that the population means are not equal:
H A : u 1 ≠ u 2
To do this, we need to set a significance level (also called alpha) that allows us to either reject or accept the alternative hypothesis. Most commonly, this value is set at 0.05.
What do you need to run an independent t-test?
In order to run an independent t-test, you need the following:
- One independent, categorical variable that has two levels/groups.
- One continuous dependent variable.
Unrelated groups
Unrelated groups, also called unpaired groups or independent groups, are groups in which the cases (e.g., participants) in each group are different. Often we are investigating differences in individuals, which means that when comparing two groups, an individual in one group cannot also be a member of the other group and vice versa. An example would be gender - an individual would have to be classified as either male or female – not both.
Assumption of normality of the dependent variable
The independent t-test requires that the dependent variable is approximately normally distributed within each group.
Note: Technically, it is the residuals that need to be normally distributed, but for an independent t-test, both will give you the same result.
You can test for this using a number of different tests, but the Shapiro-Wilks test of normality or a graphical method, such as a Q-Q Plot, are very common. You can run these tests using SPSS Statistics, the procedure for which can be found in our Testing for Normality guide. However, the t-test is described as a robust test with respect to the assumption of normality. This means that some deviation away from normality does not have a large influence on Type I error rates. The exception to this is if the ratio of the smallest to largest group size is greater than 1.5 (largest compared to smallest).
What to do when you violate the normality assumption
If you find that either one or both of your group's data is not approximately normally distributed and groups sizes differ greatly, you have two options: (1) transform your data so that the data becomes normally distributed (to do this in SPSS Statistics see our guide on Transforming Data ), or (2) run the Mann-Whitney U test which is a non-parametric test that does not require the assumption of normality (to run this test in SPSS Statistics see our guide on the Mann-Whitney U Test ).
Assumption of homogeneity of variance
The independent t-test assumes the variances of the two groups you are measuring are equal in the population. If your variances are unequal, this can affect the Type I error rate. The assumption of homogeneity of variance can be tested using Levene's Test of Equality of Variances, which is produced in SPSS Statistics when running the independent t-test procedure. If you have run Levene's Test of Equality of Variances in SPSS Statistics, you will get a result similar to that below:

This test for homogeneity of variance provides an F -statistic and a significance value ( p -value). We are primarily concerned with the significance value – if it is greater than 0.05 (i.e., p > .05), our group variances can be treated as equal. However, if p < 0.05, we have unequal variances and we have violated the assumption of homogeneity of variances.
Overcoming a violation of the assumption of homogeneity of variance
If the Levene's Test for Equality of Variances is statistically significant, which indicates that the group variances are unequal in the population, you can correct for this violation by not using the pooled estimate for the error term for the t -statistic, but instead using an adjustment to the degrees of freedom using the Welch-Satterthwaite method. In all reality, you will probably never have heard of these adjustments because SPSS Statistics hides this information and simply labels the two options as "Equal variances assumed" and "Equal variances not assumed" without explicitly stating the underlying tests used. However, you can see the evidence of these tests as below:

From the result of Levene's Test for Equality of Variances, we can reject the null hypothesis that there is no difference in the variances between the groups and accept the alternative hypothesis that there is a statistically significant difference in the variances between groups. The effect of not being able to assume equal variances is evident in the final column of the above figure where we see a reduction in the value of the t -statistic and a large reduction in the degrees of freedom (df). This has the effect of increasing the p -value above the critical significance level of 0.05. In this case, we therefore do not accept the alternative hypothesis and accept that there are no statistically significant differences between means. This would not have been our conclusion had we not tested for homogeneity of variances.

Reporting the result of an independent t-test
When reporting the result of an independent t-test, you need to include the t -statistic value, the degrees of freedom (df) and the significance value of the test ( p -value). The format of the test result is: t (df) = t -statistic, p = significance value. Therefore, for the example above, you could report the result as t (7.001) = 2.233, p = 0.061.
Fully reporting your results
In order to provide enough information for readers to fully understand the results when you have run an independent t-test, you should include the result of normality tests, Levene's Equality of Variances test, the two group means and standard deviations, the actual t-test result and the direction of the difference (if any). In addition, you might also wish to include the difference between the groups along with a 95% confidence interval. For example:
Inspection of Q-Q Plots revealed that cholesterol concentration was normally distributed for both groups and that there was homogeneity of variance as assessed by Levene's Test for Equality of Variances. Therefore, an independent t-test was run on the data with a 95% confidence interval (CI) for the mean difference. It was found that after the two interventions, cholesterol concentrations in the dietary group (6.15 ± 0.52 mmol/L) were significantly higher than the exercise group (5.80 ± 0.38 mmol/L) ( t (38) = 2.470, p = 0.018) with a difference of 0.35 (95% CI, 0.06 to 0.64) mmol/L.
To know how to run an independent t-test in SPSS Statistics, see our SPSS Statistics Independent-Samples T-Test guide. Alternatively, you can carry out an independent-samples t-test using Excel, R and RStudio .

- Quality Improvement
- Talk To Minitab
Understanding t-Tests: 1-sample, 2-sample, and Paired t-Tests
Topics: Hypothesis Testing , Data Analysis
In statistics, t-tests are a type of hypothesis test that allows you to compare means. They are called t-tests because each t-test boils your sample data down to one number, the t-value. If you understand how t-tests calculate t-values, you’re well on your way to understanding how these tests work.
In this series of posts, I'm focusing on concepts rather than equations to show how t-tests work. However, this post includes two simple equations that I’ll work through using the analogy of a signal-to-noise ratio.
Minitab Statistical Software offers the 1-sample t-test, paired t-test, and the 2-sample t-test. Let's look at how each of these t-tests reduce your sample data down to the t-value.
How 1-Sample t-Tests Calculate t-Values
Understanding this process is crucial to understanding how t-tests work. I'll show you the formula first, and then I’ll explain how it works.
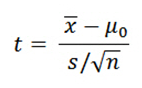
Please notice that the formula is a ratio. A common analogy is that the t-value is the signal-to-noise ratio.
Signal (a.k.a. the effect size)
The numerator is the signal. You simply take the sample mean and subtract the null hypothesis value. If your sample mean is 10 and the null hypothesis is 6, the difference, or signal, is 4.
If there is no difference between the sample mean and null value, the signal in the numerator, as well as the value of the entire ratio, equals zero. For instance, if your sample mean is 6 and the null value is 6, the difference is zero.
As the difference between the sample mean and the null hypothesis mean increases in either the positive or negative direction, the strength of the signal increases.

The denominator is the noise. The equation in the denominator is a measure of variability known as the standard error of the mean . This statistic indicates how accurately your sample estimates the mean of the population. A larger number indicates that your sample estimate is less precise because it has more random error.
This random error is the “noise.” When there is more noise, you expect to see larger differences between the sample mean and the null hypothesis value even when the null hypothesis is true . We include the noise factor in the denominator because we must determine whether the signal is large enough to stand out from it.
Signal-to-Noise ratio
Both the signal and noise values are in the units of your data. If your signal is 6 and the noise is 2, your t-value is 3. This t-value indicates that the difference is 3 times the size of the standard error. However, if there is a difference of the same size but your data have more variability (6), your t-value is only 1. The signal is at the same scale as the noise.
In this manner, t-values allow you to see how distinguishable your signal is from the noise. Relatively large signals and low levels of noise produce larger t-values. If the signal does not stand out from the noise, it’s likely that the observed difference between the sample estimate and the null hypothesis value is due to random error in the sample rather than a true difference at the population level.
A Paired t-test Is Just A 1-Sample t-Test
Many people are confused about when to use a paired t-test and how it works. I’ll let you in on a little secret. The paired t-test and the 1-sample t-test are actually the same test in disguise! As we saw above, a 1-sample t-test compares one sample mean to a null hypothesis value. A paired t-test simply calculates the difference between paired observations (e.g., before and after) and then performs a 1-sample t-test on the differences.
You can test this with this data set to see how all of the results are identical, including the mean difference, t-value, p-value, and confidence interval of the difference.
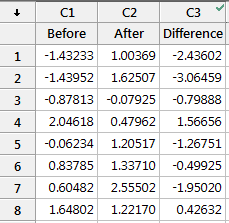
Understanding that the paired t-test simply performs a 1-sample t-test on the paired differences can really help you understand how the paired t-test works and when to use it. You just need to figure out whether it makes sense to calculate the difference between each pair of observations.
For example, let’s assume that “before” and “after” represent test scores, and there was an intervention in between them. If the before and after scores in each row of the example worksheet represent the same subject, it makes sense to calculate the difference between the scores in this fashion—the paired t-test is appropriate. However, if the scores in each row are for different subjects, it doesn’t make sense to calculate the difference. In this case, you’d need to use another test, such as the 2-sample t-test, which I discuss below.
Using the paired t-test simply saves you the step of having to calculate the differences before performing the t-test. You just need to be sure that the paired differences make sense!
When it is appropriate to use a paired t-test, it can be more powerful than a 2-sample t-test. For more information, go to Overview for paired t .
How Two-Sample T-tests Calculate T-Values
The 2-sample t-test takes your sample data from two groups and boils it down to the t-value. The process is very similar to the 1-sample t-test, and you can still use the analogy of the signal-to-noise ratio. Unlike the paired t-test, the 2-sample t-test requires independent groups for each sample.
The formula is below, and then some discussion.
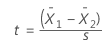
For the 2-sample t-test, the numerator is again the signal, which is the difference between the means of the two samples. For example, if the mean of group 1 is 10, and the mean of group 2 is 4, the difference is 6.
The default null hypothesis for a 2-sample t-test is that the two groups are equal. You can see in the equation that when the two groups are equal, the difference (and the entire ratio) also equals zero. As the difference between the two groups grows in either a positive or negative direction, the signal becomes stronger.
In a 2-sample t-test, the denominator is still the noise, but Minitab can use two different values. You can either assume that the variability in both groups is equal or not equal, and Minitab uses the corresponding estimate of the variability. Either way, the principle remains the same: you are comparing your signal to the noise to see how much the signal stands out.
Just like with the 1-sample t-test, for any given difference in the numerator, as you increase the noise value in the denominator, the t-value becomes smaller. To determine that the groups are different, you need a t-value that is large.
What Do t-Values Mean?
Each type of t-test uses a procedure to boil all of your sample data down to one value, the t-value. The calculations compare your sample mean(s) to the null hypothesis and incorporates both the sample size and the variability in the data. A t-value of 0 indicates that the sample results exactly equal the null hypothesis. In statistics, we call the difference between the sample estimate and the null hypothesis the effect size. As this difference increases, the absolute value of the t-value increases.
That’s all nice, but what does a t-value of, say, 2 really mean? From the discussion above, we know that a t-value of 2 indicates that the observed difference is twice the size of the variability in your data. However, we use t-tests to evaluate hypotheses rather than just figuring out the signal-to-noise ratio. We want to determine whether the effect size is statistically significant.
To see how we get from t-values to assessing hypotheses and determining statistical significance, read the other post in this series, Understanding t-Tests: t-values and t-distributions .
You Might Also Like
- Trust Center
© 2023 Minitab, LLC. All Rights Reserved.
- Terms of Use
- Privacy Policy
- Cookies Settings
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
AP®︎/College Statistics
Course: ap®︎/college statistics > unit 11.
- Hypotheses for a two-sample t test
Example of hypotheses for paired and two-sample t tests
- Writing hypotheses to test the difference of means
- Two-sample t test for difference of means
- Test statistic in a two-sample t test
- P-value in a two-sample t test
- Conclusion for a two-sample t test using a P-value
- Conclusion for a two-sample t test using a confidence interval
- Making conclusions about the difference of means
Want to join the conversation?
- Upvote Button navigates to signup page
- Downvote Button navigates to signup page
- Flag Button navigates to signup page
Video transcript

IMAGES
VIDEO
COMMENTS
Fortunately, a two sample t-test allows us to answer this question. Two Sample t-test: Formula. A two-sample t-test always uses the following null hypothesis: H 0: μ 1 = μ 2 (the two population means are equal) The alternative hypothesis can be either two-tailed, left-tailed, or right-tailed:
Two-Sample T Test Hypotheses. Null hypothesis (H 0): Two population means are equal (µ 1 = µ 2). Alternative hypothesis (H A): Two population means are not equal (µ 1 ≠ µ 2). Again, when the p-value is less than or equal to your significance level, reject the null hypothesis. The difference between the two means is statistically significant.
Revised on June 22, 2023. A t test is a statistical test that is used to compare the means of two groups. It is often used in hypothesis testing to determine whether a process or treatment actually has an effect on the population of interest, or whether two groups are different from one another. t test example.
Fortunately, a two sample t-test allows us to answer this question. Two Sample t-test: Formula. A two-sample t-test always uses the following null hypothesis: H 0: μ 1 = μ 2 (the two population means are equal) The alternative hypothesis can be either two-tailed, left-tailed, or right-tailed:
If that's below your significance level, then you would reject your null hypothesis and it would suggest the alternative that might be that, "Hey, maybe this mean "is greater than zero." On the other hand, a two-sample T test is where you're thinking about two different populations. For example, you could be thinking about a population of men ...
How Two-Sample T-tests Calculate T-Values. Use the 2-sample t-test when you want to analyze the difference between the means of two independent samples. This test is also known as the independent samples t-test. Click the link to learn more about its hypotheses, assumptions, and interpretations. Like the other t-tests, this procedure reduces ...
The results for the two-sample t-test that assumes equal variances are the same as our calculations earlier. The test statistic is 2.79996. The software shows results for a two-sided test and for one-sided tests. The two-sided test is what we want (Prob > |t|). Our null hypothesis is that the mean body fat for men and women is equal.
T-test definition, formula explanation, and assumptions. The T-test is the test, which allows us to analyze one or two sample means, depending on the type of t-test. Yes, the t-test has several types: One-sample t-test — compare the mean of one group against the specified mean generated from a population. For example, a manufacturer of mobile ...
Independent Samples T Tests Hypotheses. Independent samples t tests have the following hypotheses: Null hypothesis: The means for the two populations are equal. Alternative hypothesis: The means for the two populations are not equal.; If the p-value is less than your significance level (e.g., 0.05), you can reject the null hypothesis. The difference between the two means is statistically ...
The independent t-test, also called the two sample t-test, independent-samples t-test or student's t-test, is an inferential statistical test that determines whether there is a statistically significant difference between the means in two unrelated groups. ... The null hypothesis for the independent t-test is that the population means from the ...
The t-test for dependent samples is a statistical test for comparing the means from two dependent populations (or the difference between the means from two populations). The t-test is used when the differences are normally distributed. The samples also must be dependent. The formula for the t-test statistic is: t = D¯−μD (SD n√) t = D ...
And let's assume that we are working with a significance level of 0.05. So pause the video, and conduct the two sample T test here, to see whether there's evidence that the sizes of tomato plants differ between the fields. Alright, now let's work through this together. So like always, let's first construct our null hypothesis.
The 2-sample t-test takes your sample data from two groups and boils it down to the t-value. The process is very similar to the 1-sample t-test, and you can still use the analogy of the signal-to-noise ratio. Unlike the paired t-test, the 2-sample t-test requires independent groups for each sample. The formula is below, and then some discussion.
A one-sample t-test (to test the mean of a single group against a hypothesized mean); A two-sample t-test (to compare the means for two groups); or. A paired t-test (to check how the mean from the same group changes after some intervention). Decide on the alternative hypothesis: Two-tailed; Left-tailed; or. Right-tailed.
Courses on Khan Academy are always 100% free. Start practicing—and saving your progress—now: https://www.khanacademy.org/math/ap-statistics/xfb5d8e68:infere...
1. Two tailed test example: A factory uses two identical machines to produce plastic plates. You would expect both machines to produce the same number of plates per minute. Let μ1 = average number of plates produced by machine1 per minute. Let μ2 = average number of plates produced by machine2 per minute. We would expect μ1 to be equal to μ2.
First of all, if you have two groups, one testing one placebo, then it's 2 samples. If it is the same group before and after, then paired t-test. I'm trying to run a dependent sample t-test/paired sample t test through using data from a Qualtrics survey measuring two groups of people (one with social anxiety and one without on the effects of ...
00:37:48 - Create a two sample t-test and confidence interval with pooled variances (Example #4) 00:51:23 - Construct a two-sample t-test (Example #5) 00:59:47 - Matched Pair one sample t-test (Example #6) 01:09:38 - Use a match paired hypothesis test and provide a confidence interval for difference of means (Example #7) Practice ...
So an unusual value of t would be anything with absolute value greater than 2.04. Similarly, for 2 d.f. the bars are at +/- 4.3. The brilliance of the t-test is that if the null hypothesis is true then the two sample means and variances and the sample sizes are sufficient to compute the t-value and determine the associated p-value.
Student's t-test is a statistical test used to test whether the difference between the response of two groups is statistically significant or not. It is any statistical hypothesis test in which the test statistic follows a Student's t-distribution under the null hypothesis.It is most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in ...
If this is not the case, you should instead use the Welch's t-test calculator. To perform a two sample t-test, simply fill in the information below and then click the "Calculate" button. Enter raw data Enter summary data. Sample 1. 301, 298, 295, 297, 304, 305, 309, 298, 291, 299, 293, 304. Sample 2.
A two sample t hypothesis tests also known as independent t-test is used to analyze the difference between two unknown population means. The Two-sample T-test is used when the two small samples (n< 30) are taken from two different populations and compared. The underlying chart makes use of the T distribution.
How t-Tests Work: t-Values, t-Distributions, and Probabilities. T-tests are statistical hypothesis tests that you use to analyze one or two sample means. Depending on the t-test that you use, you can compare a sample mean to a hypothesized value, the means of two independent samples, or the difference between paired samples.
Before we can actually conduct the hypothesis test, we'll have to derive the appropriate test statistic. Theorem. The test statistic for testing the difference in two population proportions, that is, for testing the null hypothesis \(H_0:p_1-p_2=0\) is: ... the proportion of "successes" in the two samples combined. Proof. Recall that: \(\hat{p ...
The populations from which the two samples are drawn are approximately normally distributed. The two populations are independent of each other. Unlike most other hypothesis tests in this book, the F test for equality of two variances is very sensitive to deviations from normality. If the two distributions are not normal, or close, the test can ...
The appropriate set of hypotheses for Alex's significance test is option D. What is Hypothesis Testing? Hypothesis testing is the testing of the relationship between two variables for something we needed to test. There is null hypothesis and alternate hypothesis. Null hypothesis, H₀ is the statement we need to test.