1.1 Real Numbers: Algebra Essentials
- ⓐ 11 1 11 1
- ⓒ − 4 1 − 4 1
- ⓐ 4 (or 4.0), terminating;
- ⓑ 0. 615384 ¯ , 0. 615384 ¯ , repeating;
- ⓒ –0.85, terminating
- ⓐ rational and repeating;
- ⓑ rational and terminating;
- ⓒ irrational;
- ⓓ rational and terminating;
- ⓔ irrational
- ⓐ positive, irrational; right
- ⓑ negative, rational; left
- ⓒ positive, rational; right
- ⓓ negative, irrational; left
- ⓔ positive, rational; right
| a. | X | X | |||
| b. 0 | X | X | X | ||
| c. | X | X | X | X | |
| d. | X | ||||
| e. 4.763763763... | X |
- ⓐ 11, commutative property of multiplication, associative property of multiplication, inverse property of multiplication, identity property of multiplication;
- ⓑ 33, distributive property;
- ⓒ 26, distributive property;
- ⓓ 4 9 , 4 9 , commutative property of addition, associative property of addition, inverse property of addition, identity property of addition;
- ⓔ 0, distributive property, inverse property of addition, identity property of addition
| Constants | Variables | |
|---|---|---|
| a. | ||
| b. 2(L + W) | 2 | L, W |
| c. | 4 |
- ⓒ 121 3 π 121 3 π ;
- ⓐ −2 y −2 z or −2 ( y + z ) ; −2 y −2 z or −2 ( y + z ) ;
- ⓑ 2 t −1 ; 2 t −1 ;
- ⓒ 3 p q −4 p + q ; 3 p q −4 p + q ;
- ⓓ 7 r −2 s + 6 7 r −2 s + 6
A = P ( 1 + r t ) A = P ( 1 + r t )

1.2 Exponents and Scientific Notation
- ⓐ k 15 k 15
- ⓑ ( 2 y ) 5 ( 2 y ) 5
- ⓒ t 14 t 14
- ⓑ ( −3 ) 5 ( −3 ) 5
- ⓒ ( e f 2 ) 2 ( e f 2 ) 2
- ⓐ ( 3 y ) 24 ( 3 y ) 24
- ⓑ t 35 t 35
- ⓒ ( − g ) 16 ( − g ) 16
- ⓐ 1 ( −3 t ) 6 1 ( −3 t ) 6
- ⓑ 1 f 3 1 f 3
- ⓒ 2 5 k 3 2 5 k 3
- ⓐ t −5 = 1 t 5 t −5 = 1 t 5
- ⓑ 1 25 1 25
- ⓐ g 10 h 15 g 10 h 15
- ⓑ 125 t 3 125 t 3
- ⓒ −27 y 15 −27 y 15
- ⓓ 1 a 18 b 21 1 a 18 b 21
- ⓔ r 12 s 8 r 12 s 8
- ⓐ b 15 c 3 b 15 c 3
- ⓑ 625 u 32 625 u 32
- ⓒ −1 w 105 −1 w 105
- ⓓ q 24 p 32 q 24 p 32
- ⓔ 1 c 20 d 12 1 c 20 d 12
- ⓐ v 6 8 u 3 v 6 8 u 3
- ⓑ 1 x 3 1 x 3
- ⓒ e 4 f 4 e 4 f 4
- ⓓ 27 r s 27 r s
- ⓕ 16 h 10 49 16 h 10 49
- ⓐ $ 1.52 × 10 5 $ 1.52 × 10 5
- ⓑ 7.158 × 10 9 7.158 × 10 9
- ⓒ $ 8.55 × 10 13 $ 8.55 × 10 13
- ⓓ 3.34 × 10 −9 3.34 × 10 −9
- ⓔ 7.15 × 10 −8 7.15 × 10 −8
- ⓐ 703 , 000 703 , 000
- ⓑ −816 , 000 , 000 , 000 −816 , 000 , 000 , 000
- ⓒ −0.000 000 000 000 39 −0.000 000 000 000 39
- ⓓ 0.000008 0.000008
- ⓐ − 8.475 × 10 6 − 8.475 × 10 6
- ⓑ 8 × 10 − 8 8 × 10 − 8
- ⓒ 2.976 × 10 13 2.976 × 10 13
- ⓓ − 4.3 × 10 6 − 4.3 × 10 6
- ⓔ ≈ 1.24 × 10 15 ≈ 1.24 × 10 15
Number of cells: 3 × 10 13 ; 3 × 10 13 ; length of a cell: 8 × 10 −6 8 × 10 −6 m; total length: 2.4 × 10 8 2.4 × 10 8 m or 240 , 000 , 000 240 , 000 , 000 m.
1.3 Radicals and Rational Exponents
5 | x | | y | 2 y z . 5 | x | | y | 2 y z . Notice the absolute value signs around x and y ? That’s because their value must be positive!
10 | x | 10 | x |
x 2 3 y 2 . x 2 3 y 2 . We do not need the absolute value signs for y 2 y 2 because that term will always be nonnegative.
b 4 3 a b b 4 3 a b
14 −7 3 14 −7 3
- ⓒ 88 9 3 88 9 3
( 9 ) 5 = 3 5 = 243 ( 9 ) 5 = 3 5 = 243
x ( 5 y ) 9 2 x ( 5 y ) 9 2
28 x 23 15 28 x 23 15
1.4 Polynomials
The degree is 6, the leading term is − x 6 , − x 6 , and the leading coefficient is −1. −1.
2 x 3 + 7 x 2 −4 x −3 2 x 3 + 7 x 2 −4 x −3
−11 x 3 − x 2 + 7 x −9 −11 x 3 − x 2 + 7 x −9
3 x 4 −10 x 3 −8 x 2 + 21 x + 14 3 x 4 −10 x 3 −8 x 2 + 21 x + 14
3 x 2 + 16 x −35 3 x 2 + 16 x −35
16 x 2 −8 x + 1 16 x 2 −8 x + 1
4 x 2 −49 4 x 2 −49
6 x 2 + 21 x y −29 x −7 y + 9 6 x 2 + 21 x y −29 x −7 y + 9
1.5 Factoring Polynomials
( b 2 − a ) ( x + 6 ) ( b 2 − a ) ( x + 6 )
( x −6 ) ( x −1 ) ( x −6 ) ( x −1 )
- ⓐ ( 2 x + 3 ) ( x + 3 ) ( 2 x + 3 ) ( x + 3 )
- ⓑ ( 3 x −1 ) ( 2 x + 1 ) ( 3 x −1 ) ( 2 x + 1 )
( 7 x −1 ) 2 ( 7 x −1 ) 2
( 9 y + 10 ) ( 9 y − 10 ) ( 9 y + 10 ) ( 9 y − 10 )
( 6 a + b ) ( 36 a 2 −6 a b + b 2 ) ( 6 a + b ) ( 36 a 2 −6 a b + b 2 )
( 10 x − 1 ) ( 100 x 2 + 10 x + 1 ) ( 10 x − 1 ) ( 100 x 2 + 10 x + 1 )
( 5 a −1 ) − 1 4 ( 17 a −2 ) ( 5 a −1 ) − 1 4 ( 17 a −2 )
1.6 Rational Expressions
1 x + 6 1 x + 6
( x + 5 ) ( x + 6 ) ( x + 2 ) ( x + 4 ) ( x + 5 ) ( x + 6 ) ( x + 2 ) ( x + 4 )
2 ( x −7 ) ( x + 5 ) ( x −3 ) 2 ( x −7 ) ( x + 5 ) ( x −3 )
x 2 − y 2 x y 2 x 2 − y 2 x y 2
1.1 Section Exercises
irrational number. The square root of two does not terminate, and it does not repeat a pattern. It cannot be written as a quotient of two integers, so it is irrational.
The Associative Properties state that the sum or product of multiple numbers can be grouped differently without affecting the result. This is because the same operation is performed (either addition or subtraction), so the terms can be re-ordered.
−14 y − 11 −14 y − 11
−4 b + 1 −4 b + 1
43 z − 3 43 z − 3
9 y + 45 9 y + 45
−6 b + 6 −6 b + 6
16 x 3 16 x 3
1 2 ( 40 − 10 ) + 5 1 2 ( 40 − 10 ) + 5
irrational number
g + 400 − 2 ( 600 ) = 1200 g + 400 − 2 ( 600 ) = 1200
inverse property of addition
1.2 Section Exercises
No, the two expressions are not the same. An exponent tells how many times you multiply the base. So 2 3 2 3 is the same as 2 × 2 × 2 , 2 × 2 × 2 , which is 8. 3 2 3 2 is the same as 3 × 3 , 3 × 3 , which is 9.
It is a method of writing very small and very large numbers.
12 40 12 40
1 7 9 1 7 9
3.14 × 10 − 5 3.14 × 10 − 5
16,000,000,000
b 6 c 8 b 6 c 8
a b 2 d 3 a b 2 d 3
q 5 p 6 q 5 p 6
y 21 x 14 y 21 x 14
72 a 2 72 a 2
c 3 b 9 c 3 b 9
y 81 z 6 y 81 z 6
1.0995 × 10 12 1.0995 × 10 12
0.00000000003397 in.
12,230,590,464 m 66 m 66
a 14 1296 a 14 1296
n a 9 c n a 9 c
1 a 6 b 6 c 6 1 a 6 b 6 c 6
0.000000000000000000000000000000000662606957
1.3 Section Exercises
When there is no index, it is assumed to be 2 or the square root. The expression would only be equal to the radicand if the index were 1.
The principal square root is the nonnegative root of the number.
9 5 5 9 5 5
6 10 19 6 10 19
− 1 + 17 2 − 1 + 17 2
7 2 3 7 2 3
20 x 2 20 x 2
17 m 2 m 17 m 2 m
2 b a 2 b a
15 x 7 15 x 7
5 y 4 2 5 y 4 2
4 7 d 7 d 4 7 d 7 d
2 2 + 2 6 x 1 −3 x 2 2 + 2 6 x 1 −3 x
− w 2 w − w 2 w
3 x − 3 x 2 3 x − 3 x 2
5 n 5 5 5 n 5 5
9 m 19 m 9 m 19 m
2 3 d 2 3 d
3 2 x 2 4 2 3 2 x 2 4 2
6 z 2 3 6 z 2 3
−5 2 −6 7 −5 2 −6 7
m n c a 9 c m n m n c a 9 c m n
2 2 x + 2 4 2 2 x + 2 4
1.4 Section Exercises
The statement is true. In standard form, the polynomial with the highest value exponent is placed first and is the leading term. The degree of a polynomial is the value of the highest exponent, which in standard form is also the exponent of the leading term.
Use the distributive property, multiply, combine like terms, and simplify.
4 x 2 + 3 x + 19 4 x 2 + 3 x + 19
3 w 2 + 30 w + 21 3 w 2 + 30 w + 21
11 b 4 −9 b 3 + 12 b 2 −7 b + 8 11 b 4 −9 b 3 + 12 b 2 −7 b + 8
24 x 2 −4 x −8 24 x 2 −4 x −8
24 b 4 −48 b 2 + 24 24 b 4 −48 b 2 + 24
99 v 2 −202 v + 99 99 v 2 −202 v + 99
8 n 3 −4 n 2 + 72 n −36 8 n 3 −4 n 2 + 72 n −36
9 y 2 −42 y + 49 9 y 2 −42 y + 49
16 p 2 + 72 p + 81 16 p 2 + 72 p + 81
9 y 2 −36 y + 36 9 y 2 −36 y + 36
16 c 2 −1 16 c 2 −1
225 n 2 −36 225 n 2 −36
−16 m 2 + 16 −16 m 2 + 16
121 q 2 −100 121 q 2 −100
16 t 4 + 4 t 3 −32 t 2 − t + 7 16 t 4 + 4 t 3 −32 t 2 − t + 7
y 3 −6 y 2 − y + 18 y 3 −6 y 2 − y + 18
3 p 3 − p 2 −12 p + 10 3 p 3 − p 2 −12 p + 10
a 2 − b 2 a 2 − b 2
16 t 2 −40 t u + 25 u 2 16 t 2 −40 t u + 25 u 2
4 t 2 + x 2 + 4 t −5 t x − x 4 t 2 + x 2 + 4 t −5 t x − x
24 r 2 + 22 r d −7 d 2 24 r 2 + 22 r d −7 d 2
32 x 2 −4 x −3 32 x 2 −4 x −3 m 2
32 t 3 − 100 t 2 + 40 t + 38 32 t 3 − 100 t 2 + 40 t + 38
a 4 + 4 a 3 c −16 a c 3 −16 c 4 a 4 + 4 a 3 c −16 a c 3 −16 c 4
1.5 Section Exercises
The terms of a polynomial do not have to have a common factor for the entire polynomial to be factorable. For example, 4 x 2 4 x 2 and −9 y 2 −9 y 2 don’t have a common factor, but the whole polynomial is still factorable: 4 x 2 −9 y 2 = ( 2 x + 3 y ) ( 2 x −3 y ) . 4 x 2 −9 y 2 = ( 2 x + 3 y ) ( 2 x −3 y ) .
Divide the x x term into the sum of two terms, factor each portion of the expression separately, and then factor out the GCF of the entire expression.
10 m 3 10 m 3
( 2 a −3 ) ( a + 6 ) ( 2 a −3 ) ( a + 6 )
( 3 n −11 ) ( 2 n + 1 ) ( 3 n −11 ) ( 2 n + 1 )
( p + 1 ) ( 2 p −7 ) ( p + 1 ) ( 2 p −7 )
( 5 h + 3 ) ( 2 h −3 ) ( 5 h + 3 ) ( 2 h −3 )
( 9 d −1 ) ( d −8 ) ( 9 d −1 ) ( d −8 )
( 12 t + 13 ) ( t −1 ) ( 12 t + 13 ) ( t −1 )
( 4 x + 10 ) ( 4 x − 10 ) ( 4 x + 10 ) ( 4 x − 10 )
( 11 p + 13 ) ( 11 p − 13 ) ( 11 p + 13 ) ( 11 p − 13 )
( 19 d + 9 ) ( 19 d − 9 ) ( 19 d + 9 ) ( 19 d − 9 )
( 12 b + 5 c ) ( 12 b − 5 c ) ( 12 b + 5 c ) ( 12 b − 5 c )
( 7 n + 12 ) 2 ( 7 n + 12 ) 2
( 15 y + 4 ) 2 ( 15 y + 4 ) 2
( 5 p − 12 ) 2 ( 5 p − 12 ) 2
( x + 6 ) ( x 2 − 6 x + 36 ) ( x + 6 ) ( x 2 − 6 x + 36 )
( 5 a + 7 ) ( 25 a 2 − 35 a + 49 ) ( 5 a + 7 ) ( 25 a 2 − 35 a + 49 )
( 4 x − 5 ) ( 16 x 2 + 20 x + 25 ) ( 4 x − 5 ) ( 16 x 2 + 20 x + 25 )
( 5 r + 12 s ) ( 25 r 2 − 60 r s + 144 s 2 ) ( 5 r + 12 s ) ( 25 r 2 − 60 r s + 144 s 2 )
( 2 c + 3 ) − 1 4 ( −7 c − 15 ) ( 2 c + 3 ) − 1 4 ( −7 c − 15 )
( x + 2 ) − 2 5 ( 19 x + 10 ) ( x + 2 ) − 2 5 ( 19 x + 10 )
( 2 z − 9 ) − 3 2 ( 27 z − 99 ) ( 2 z − 9 ) − 3 2 ( 27 z − 99 )
( 14 x −3 ) ( 7 x + 9 ) ( 14 x −3 ) ( 7 x + 9 )
( 3 x + 5 ) ( 3 x −5 ) ( 3 x + 5 ) ( 3 x −5 )
( 2 x + 5 ) 2 ( 2 x − 5 ) 2 ( 2 x + 5 ) 2 ( 2 x − 5 ) 2
( 4 z 2 + 49 a 2 ) ( 2 z + 7 a ) ( 2 z − 7 a ) ( 4 z 2 + 49 a 2 ) ( 2 z + 7 a ) ( 2 z − 7 a )
1 ( 4 x + 9 ) ( 4 x −9 ) ( 2 x + 3 ) 1 ( 4 x + 9 ) ( 4 x −9 ) ( 2 x + 3 )
1.6 Section Exercises
You can factor the numerator and denominator to see if any of the terms can cancel one another out.
True. Multiplication and division do not require finding the LCD because the denominators can be combined through those operations, whereas addition and subtraction require like terms.
y + 5 y + 6 y + 5 y + 6
3 b + 3 3 b + 3
x + 4 2 x + 2 x + 4 2 x + 2
a + 3 a − 3 a + 3 a − 3
3 n − 8 7 n − 3 3 n − 8 7 n − 3
c − 6 c + 6 c − 6 c + 6
d 2 − 25 25 d 2 − 1 d 2 − 25 25 d 2 − 1
t + 5 t + 3 t + 5 t + 3
6 x − 5 6 x + 5 6 x − 5 6 x + 5
p + 6 4 p + 3 p + 6 4 p + 3
2 d + 9 d + 11 2 d + 9 d + 11
12 b + 5 3 b −1 12 b + 5 3 b −1
4 y −1 y + 4 4 y −1 y + 4
10 x + 4 y x y 10 x + 4 y x y
9 a − 7 a 2 − 2 a − 3 9 a − 7 a 2 − 2 a − 3
2 y 2 − y + 9 y 2 − y − 2 2 y 2 − y + 9 y 2 − y − 2
5 z 2 + z + 5 z 2 − z − 2 5 z 2 + z + 5 z 2 − z − 2
x + 2 x y + y x + x y + y + 1 x + 2 x y + y x + x y + y + 1
2 b + 7 a a b 2 2 b + 7 a a b 2
18 + a b 4 b 18 + a b 4 b
a − b a − b
3 c 2 + 3 c − 2 2 c 2 + 5 c + 2 3 c 2 + 3 c − 2 2 c 2 + 5 c + 2
15 x + 7 x −1 15 x + 7 x −1
x + 9 x −9 x + 9 x −9
1 y + 2 1 y + 2
Review Exercises
y = 24 y = 24
3 a 6 3 a 6
x 3 32 y 3 x 3 32 y 3
1.634 × 10 7 1.634 × 10 7
4 2 5 4 2 5
7 2 50 7 2 50
3 x 3 + 4 x 2 + 6 3 x 3 + 4 x 2 + 6
5 x 2 − x + 3 5 x 2 − x + 3
k 2 − 3 k − 18 k 2 − 3 k − 18
x 3 + x 2 + x + 1 x 3 + x 2 + x + 1
3 a 2 + 5 a b − 2 b 2 3 a 2 + 5 a b − 2 b 2
4 a 2 4 a 2
( 4 a − 3 ) ( 2 a + 9 ) ( 4 a − 3 ) ( 2 a + 9 )
( x + 5 ) 2 ( x + 5 ) 2
( 2 h − 3 k ) 2 ( 2 h − 3 k ) 2
( p + 6 ) ( p 2 − 6 p + 36 ) ( p + 6 ) ( p 2 − 6 p + 36 )
( 4 q − 3 p ) ( 16 q 2 + 12 p q + 9 p 2 ) ( 4 q − 3 p ) ( 16 q 2 + 12 p q + 9 p 2 )
( p + 3 ) 1 3 ( −5 p − 24 ) ( p + 3 ) 1 3 ( −5 p − 24 )
x + 3 x − 4 x + 3 x − 4
m + 2 m − 3 m + 2 m − 3
6 x + 10 y x y 6 x + 10 y x y
Practice Test
x = –2 x = –2
3 x 4 3 x 4
13 q 3 − 4 q 2 − 5 q 13 q 3 − 4 q 2 − 5 q
n 3 − 6 n 2 + 12 n − 8 n 3 − 6 n 2 + 12 n − 8
( 4 x + 9 ) ( 4 x − 9 ) ( 4 x + 9 ) ( 4 x − 9 )
( 3 c − 11 ) ( 9 c 2 + 33 c + 121 ) ( 3 c − 11 ) ( 9 c 2 + 33 c + 121 )
4 z − 3 2 z − 1 4 z − 3 2 z − 1
3 a + 2 b 3 b 3 a + 2 b 3 b
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites
- Authors: Jay Abramson
- Publisher/website: OpenStax
- Book title: College Algebra
- Publication date: Feb 13, 2015
- Location: Houston, Texas
- Book URL: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites
- Section URL: https://openstax.org/books/college-algebra/pages/chapter-1
© Dec 8, 2021 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

- Big Ideas Math Algebra 1, 2015
- Big Ideas Math Algebra 1, 2013
- Big Ideas Math Algebra 1 Virginia
- Big Ideas Math Algebra 1 Texas
- Big Ideas Math Algebra 1 A Bridge to Success
- Core Connections Algebra 1, 2013
- Houghton Mifflin Harcourt Algebra 1, 2015
- Holt McDougal Algebra 1, 2011
- McDougal Littell Algebra 1, 1999
- McGraw Hill Glencoe Algebra 1, 2012
- McGraw Hill Glencoe Algebra 1, 2017
- McGraw Hill Glencoe Algebra 1 Texas, 2016
- Pearson Algebra 1 Common Core, 2011
- Pearson Algebra 1 Common Core, 2015
- Precalculus
- Signup / Login

How to Use a Math Medic Answer Key
Written by Luke Wilcox published 3 years ago
Answer key might be the wrong term here. Sure, the Math Medic answer keys do provide the correct answers to the questions for a lesson, but they have been carefully designed to do much more than this. They are meant to be the official guide to teaching the lesson, providing specific instructions for what to do and say to make a successful learning experience for your students.
Before we look at the details of the answer key, let's make sure we understand the instructional model first.

Experience First, Formalize Later (EFFL)
A typical Math Medic lesson always has the same four parts: Activity, Debrief Activity, QuickNotes, and Check Your Understanding. Here are the cliff notes:
Activity: Students are in groups of 2 - 4 working collaboratively through the questions in the Activity. The teacher is checking in with groups and using questions, prompts, and cues to get students to refine their communication and understanding. As groups finish the activity, the teacher asks students to go to the whiteboard to write up their answers to the questions.
Debrief Activity: In the whole group setting, the teacher leads a discussion about the student responses to the questions in the activity, often asking students to explain their thinking and reasoning about their answers. The teacher then formalizes the learning by highlighting key concepts and introducing new vocabulary, notation, and formulas.
QuickNotes: The teacher uses direct instruction to summarize the learning from the activity in the QuickNotes box - making direct connections to the learning targets for the lesson.
Check Your Understanding: Students are then asked to apply their learning from the lesson to a new context in the Check Your Understanding (CYU) problem. This can be done individually or in small groups. The CYU is very flexible in it's use, as it can be used as an exit ticket, a homework problem, or a quick review the next day.
How Do I See EFFL in the Answer Key?
You will see EFFL in the answer key like this:
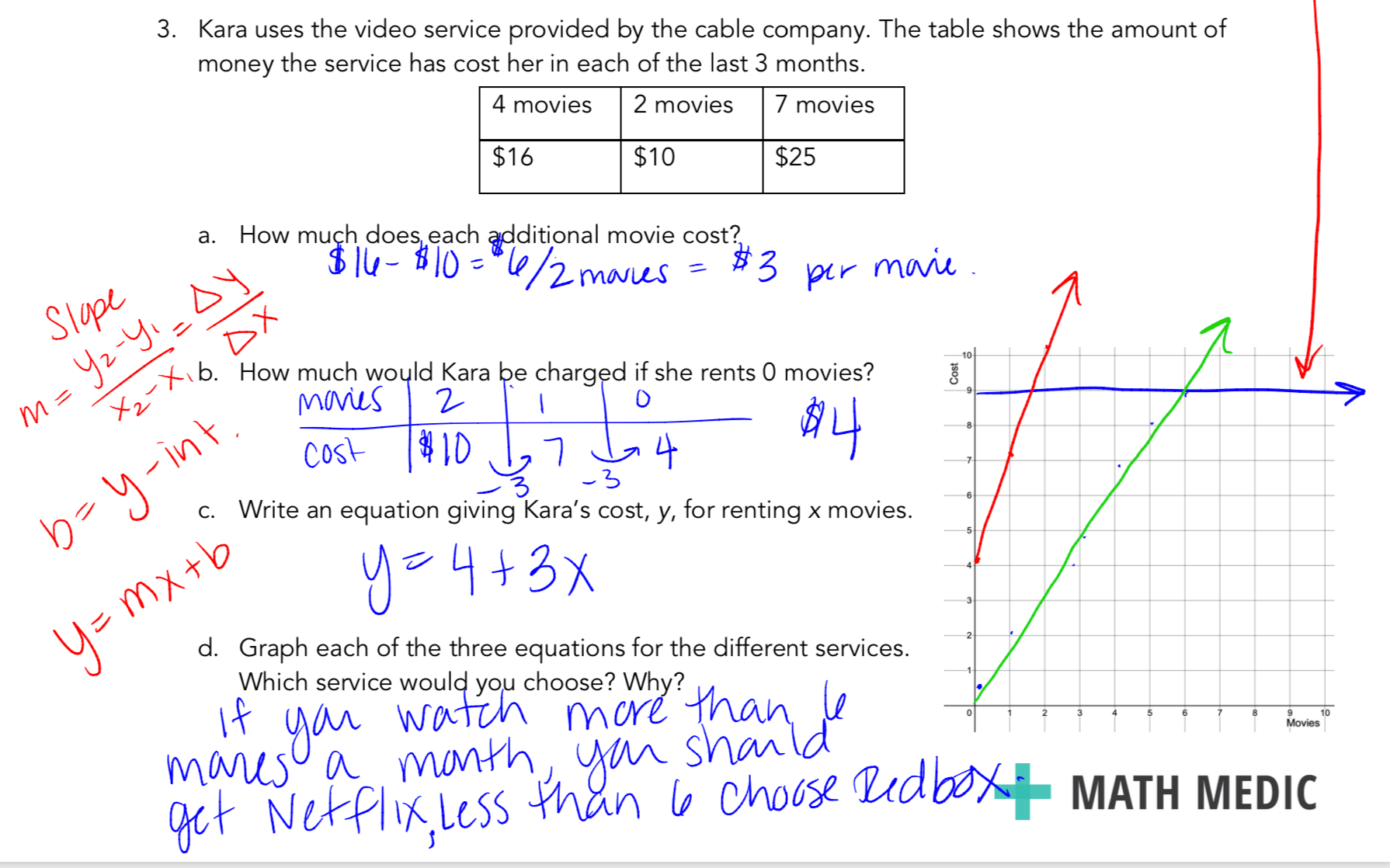
Anything written in blue is something we expect our students to produce. This might not be quite what we expect by the end of the lesson, but provides us with a starting point when we move to formalization.
Anything written in red is an idea added by the teacher - the formalization of the learning that happened during the Activity. Students are expected to add these "notes" to their Activity using a red pen or marker.
What Do Students Write Down For Notes?
By the end of the lesson, students will have written down everything you see on the Math Medic Answer Keys. The most important transition is when students finish the Activity and we move to Debrief Activity. "Students, now is the time for you to put down your pencils and get out your your red Paper Mate flair pens" We give each student a Paper Mate flair pen at the beginning of the school year and tell them they must cherish and protect it with their life. They all think we should be sponsored by Paper Mate (anyone have any leads on this?)
The lessons you see on Math Medic are all of the notes we use with our students. We do not have some secret collection of guided notes.
Do Students Have Access to Answer Keys?
Yes! Any student can create a free Math Medic account to get access to the answer keys. We often send students to the website when they are absent from a lesson or when we don't quite finish the lesson in class. We are comfortable with students having access to these answer keys because we do not think Math Medic lessons should be used as a summative assessment or be used for a grade (unless it's for completion). Our lessons are meant to be the first steps in the formative process of learning new concepts.
Math Medic Help

Home > CCA > Chapter 1 > Lesson 1.1.1
Lesson 1.1.1, lesson 1.1.2, lesson 1.1.3, lesson 1.2.1, lesson 1.2.2, lesson 1.2.3, lesson 1.2.4, lesson 1.2.5.
© 2022 CPM Educational Program. All rights reserved.
- 888-309-8227
- 732-384-0146
New User Registration
Forgot Password
Textbook Resources
| Carolina Biological Supply Company | |||
| Carolina Biological Supply Company | |||
| Carolina Biological Supply Company | |||
| Carolina Biological Supply Company | |||
| Carolina Biological Supply Company | |||
| Pearson Education, Inc. | |||
| Pearson Education, Inc. | |||
| Scott Foresman Addison Wesley | |||
| Pearson | |||
| SRA McGraw-Hill | |||
| Mc-Graw Hill | |||
| McGraw-Hill | |||
| McGraw-Hill | |||
| Houghton Mifflin Harcourt | |||
| Houghton Mifflin Harcourt | |||
| Pearson | |||
| Pearson | |||
| Pearson | |||
| Pearson | |||
| Pearson | |||
| Pearson | |||
| Pearson | |||
| Pearson | |||
| Pearson | |||
| Houghton Mifflin Harcourt | |||
| Houghton Mifflin Harcourt | |||
| Houghton Mifflin Harcourt | |||
| Marshall Cavendish | |||
| Marshall Cavendish | |||
| McGraw-Hill | |||
| McGraw-Hill | |||
| Houghton Mifflin Harcourt | |||
| Houghton Mifflin Harcourt | |||
| Houghton Mifflin Harcourt | |||
| Pearson | |||
| Pearson | |||
| Houghton Mifflin Harcourt | |||
| Scott Foresman-Addison Wesley | |||
| Harcourt School Publishers | |||
| Macmillan McGraw-Hill | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| lumos learning | |||
| lumos learning | |||
| Barron's Educational Series; Csm edition (November 1, 2016) | |||
| CreateSpace Independent Publishing Platform (September 13, 2015) | |||
| CreateSpace Independent Publishing Platform (November 11, 2015) | |||
| Barron's Educational Series; Csm Wkb edition (January 1, 2015) | |||
| CreateSpace Independent Publishing Platform (January 1, 2014) | |||
| Kumon Publishing North America; Workbook edition (June 5, 2008) | |||
| Thinking Kids; Csm edition (January 5, 2015) | |||
| Spectrum; Csm Wkb edition (August 15, 2014) | |||
| Spectrum; Csm edition (December 2, 2013) | |||
| Kumon Publishing North America; Workbook edition (June 5, 2008) | |||
| Scholastic Teaching Resources (Teaching (March 1, 2010) | |||
| Sylvan Learning Publishing; Workbook edition (January 6, 2009) | |||
| Brighter Child; Act Csm Wk edition (March 12, 2015) | |||
| CreateSpace Independent Publishing Platform (February 4, 2016) | |||
| Sylvan Learning Publishing; 1 edition (July 6, 2010) | |||
| Sylvan Learning Publishing; Workbook edition (January 6, 2009) | |||
| Teacher Created Resources (May 1, 2009) | |||
| Shell Education; 1 edition (October 1, 2012) | |||
| Carson-Dellosa Publishing; Act Csm Wk edition (February 5, 2015) | |||
| Carson-Dellosa Publishing; Csm edition (March 26, 2015) | |||
| Summer Bridge Activities | |||
| Workman Publishing |
| Carolina Biological Supply Company | |||
| Carolina Biological Supply Company | |||
| Carolina Biological Supply Company | |||
| Carolina Biological Supply Company | |||
| Carolina Biological Supply Company | |||
| Pearson Education, Inc. | |||
| Pearson Education, Inc. | |||
| Scott Foresman Addison Wesley | |||
| Pearson | |||
| SRA McGraw-Hill | |||
| Mc-Graw Hill | |||
| Mc-Graw Hill | |||
| McGraw Hill | |||
| Houghton Mifflin Harcourt | |||
| Houghton Mifflin Harcourt | |||
| Houghton Mifflin Harcourt | |||
| Pearson | |||
| Pearson | |||
| Pearson | |||
| Pearson | |||
| Pearson | |||
| Pearson | |||
| Pearson | |||
| Pearson | |||
| Pearson | |||
| Houghton Mifflin Harcourt | |||
| Houghton Mifflin Harcourt | |||
| Houghton Mifflin Harcourt | |||
| Marshall Cavendish | |||
| Marshall Cavendish | |||
| McGraw-Hill | |||
| McGraw-Hill | |||
| Houghton Mifflin Harcourt | |||
| Pearson | |||
| Pearson | |||
| Houghton Mifflin Harcourt | |||
| Scott Foresman-Addison Wesley | |||
| Harcourt School Publishers | |||
| Macmillan McGraw-Hill | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| lumos learning | |||
| lumos learning | |||
| Scholastic Teaching Resources (Teaching (March 1, 2010) | |||
| Workman Publishing Company; Ages 9-10 edition (July 9, 2008) | |||
| CreateSpace Independent Publishing Platform (April 19, 2013) | |||
| Frank Schaffer Publications; CSM WKB edition (January 3, 2012) | |||
| Carson-Dellosa Publishing (January 3, 2011) | |||
| Kumon Publishing North America; Workbook edition (June 5, 2008) | |||
| Carson-Dellosa Publishing (January 3, 2011) | |||
| Spectrum (December 2, 2013) | |||
| Sylvan Learning Publishing; Student/Stdy Gde edition (January 6, 2009) | |||
| Spectrum; Csm Wkb edition (August 15, 2014) | |||
| American Education Publishing (February 16, 2009) | |||
| Carson-Dellosa Publishing (September 17, 2013) | |||
| Summer Bridge Activities | |||
| Workman Publishing |
| Carolina Biological Supply Company | |||
| Carolina Biological Supply Company | |||
| Carolina Biological Supply Company | |||
| Carolina Biological Supply Company | |||
| Carolina Biological Supply Company | |||
| Pearson Education, Inc. | |||
| Pearson Education, Inc. | |||
| Scott Foresman Addison Wesley | |||
| Pearson | |||
| SRA McGraw-Hill | |||
| Mc-Graw Hill | |||
| McGraw Hill | |||
| McGraw Hill | |||
| Houghton Mifflin Harcourt | |||
| Houghton Mifflin Harcourt | |||
| Houghton Mifflin Harcourt | |||
| Pearson | |||
| Pearson | |||
| Pearson | |||
| Pearson | |||
| Pearson | |||
| Pearson | |||
| Pearson | |||
| Pearson | |||
| Pearson | |||
| Houghton Mifflin Harcourt | |||
| Houghton Mifflin Harcourt | |||
| Houghton Mifflin Harcourt | |||
| Marshall Cavendish | |||
| Marshall Cavendish | |||
| McGraw-Hill | |||
| McGraw-Hill | |||
| Houghton Mifflin Harcourt | |||
| Pearson | |||
| Houghton Mifflin Harcourt | |||
| Scott Foresman-Addison Wesley | |||
| Harcourt School Publishers | |||
| Macmillan McGraw-Hill | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| lumos learning | |||
| lumos learning | |||
| Barron's Educational Series (January 1, 2015) | |||
| CreateSpace Independent Publishing Platform (August 23, 2013) | |||
| Spectrum; Csm Wkb edition (August 15, 2014) | |||
| Barron's Educational Series (September 1, 2016) | |||
| CreateSpace Independent Publishing Platform; Workbook edition (September 16, 2016) | |||
| Carson-Dellosa Publishing (July 16, 2015) | |||
| Thinking Kids; Csm Wkb edition (January 15, 2015) | |||
| Frank Schaffer Publications; Workbook edition (June 1, 2009) | |||
| McGraw-Hill Education (March 13, 2012) | |||
| Spectrum; Csm Wkb edition (December 2, 2013) | |||
| Spectrum; Csm Wkb edition (August 15, 2014) | |||
| Carson-Dellosa Publishing (January 15, 2015) | |||
| Frank Schaffer Publications; Csm edition (January 3, 2012) | |||
| Frank Schaffer Publications; Csm edition (January 3, 2012) | |||
| Frank Schaffer Publications (January 3, 2012) | |||
| Frank Schaffer Publications (January 3, 2012) | |||
| Carson-Dellosa Publishing; Csm edition (July 7, 2015) | |||
| Carson-Dellosa Publishing; Workbook edition (September 17, 2013) | |||
| Summer Bridge Activities | |||
| Workman Publishing |
| Big Ideas Learning | |||
| Pearson | |||
| Pearson Education, Inc. | |||
| Pearson Education, Inc. | |||
| Scott Foresman Addison Wesley | |||
| McGraw Hill | |||
| McGraw Hill | |||
| McGraw-Hill | |||
| Houghton Mifflin Harcourt | |||
| Glencoe McGraw-Hill | |||
| McGraw-Hill | |||
| McGraw-Hill | |||
| Glencoe McGraw-Hill | |||
| Houghton Mifflin Harcourt | |||
| Houghton Mifflin Harcourt | |||
| Houghton Mifflin Harcourt | |||
| Holt McDougal | |||
| Holt McDougal HMH | |||
| Glencoe McGraw-Hill | |||
| Glencoe McGraw-Hill | |||
| Glencoe McGraw-Hill | |||
| Marshall Cavendish | |||
| Marshall Cavendish | |||
| McDougal Littell | |||
| SMc curriculum | |||
| SMc curriculum | |||
| SMc curriculum | |||
| Prentice Hall | |||
| Prentice Hall | |||
| Pearson | |||
| Pearson | |||
| Glencoe McGraw-Hill - McGraw-Hil Education | |||
| Voyager-Sopris Learning | |||
| Voyager-Sopris Learning | |||
| Voyager-Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| lumos learning | |||
| lumos learning | |||
| Barrons Test Prep; Csm edition | |||
| Florida Department of Education | |||
| McDougal Littell/Houghton Mifflin | |||
| Pennsylvania Department of Education(Mometrix Media Llc; Study Guide edition) | |||
| The Indiana Department of Education | |||
| the Partnership for Assessment of Readiness for College and Careers | |||
| Florida Department of Education | |||
| The Indiana Department of Education | |||
| Summer Bridge Activities | |||
| Workman Publishing |
| Big Ideas Learning | |||
| Pearson | |||
| Houghton Mifflin Harcourt | |||
| Glencoe/McGraw-Hill | |||
| McGraw-Hill | |||
| McGraw Hill Glencoe | |||
| Houghton Mifflin Harcourt | |||
| Houghton Mifflin Harcourt | |||
| Holt McDougal | |||
| Glencoe/McGraw-Hill | |||
| Glencoe McGraw-Hill | |||
| Glencoe/McGraw-Hill | |||
| Marshall Cavendish | |||
| Marshall Cavendish | |||
| McDougal Littell | |||
| SMc curriculum | |||
| SMc curriculum | |||
| SMc curriculum | |||
| Prentice Hall | |||
| Prentice Hall | |||
| Glencoe/McGraw-Hill | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| lumos learning | |||
| lumos learning | |||
| Barron's Educational Series | |||
| SAXON PUBLISHERS | |||
| Saxon Pub; 3 edition | |||
| Holt McDougal; Student edition | |||
| McDougal Littell/Houghton Mifflin | |||
| Florida Department of Education | |||
| The Indiana Department of Education | |||
| Mometrix Media Llc; Study Guide edition | |||
| Pennsylvania Department of Education | |||
| Florida Department of Education | |||
| Pennsylvania Department of Education | |||
| Mometrix Media Llc; Crds edition | |||
| Ohio Department of Education | |||
| Summer Bridge Activities |
| Big Ideas Learning | |||
| Pearson | |||
| Pearson | |||
| Houghton Mifflin Harcourt | |||
| Glencoe/McGraw-Hill | |||
| McGraw-Hill | |||
| McGraw-Hill | |||
| Houghton Mifflin Harcourt | |||
| Houghton Mifflin Harcourt | |||
| Holt McDougal | |||
| Glencoe/McGraw-Hill | |||
| Glencoe McGraw-Hill | |||
| Glencoe/McGraw-Hill | |||
| Marshall Cavendish | |||
| Marshall Cavendish | |||
| SNc curriculum | |||
| SMc curriculum | |||
| SMc curriculum | |||
| Prentice Hall | |||
| Prentice Hall | |||
| Glencoe/McGraw-Hill | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Voyager Sopris Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| Lumos Learning | |||
| lumos learning | |||
| lumos learning | |||
| McDougal Littell/Houghton Mifflin | |||
| Holt McDougal; Student edition | |||
| Barrons Test Prep | |||
| McDougal Littell/Houghton Mifflin | |||
| Florida Department of Education | |||
| The Indiana Department of Education | |||
| Pennsylvania Department of Education | |||
| Florida Department of Education | |||
| Mometrix Media Llc; Crds edition | |||
| Pennsylvania Department of Education | |||
| The Indiana Department of Education | |||
| Summer Bridge Activities |
textbook resources
- Call us toll-free
- FAQs – Frequently Asked Questions
- Contact Lumos Learning – Proven Study Programs by Expert Teachers
Follow us: Lumos Learning -->
- 2024 © Lumos Learning
- Privacy Policy - Terms of Service - Disclaimers
PARCC® is a registered trademark of PARCC, Inc. Lumos Learning, is not owned by or affiliated in any fashion with PARCC, Inc... Read More
PARCC® is a registered trademark of PARCC, Inc. Lumos Learning, is not owned by or affiliated in any fashion with PARCC, Inc., the Partnership for the Assessment of Readiness for College and Careers, nor any state of the Union. Neither PARCC, Inc., nor The Partnership for the Assessment of Readiness for College and Careers, nor any member state has endorsed this product. No portion of any fees or charges paid for any products or services Lumos Learning offers will be paid or inure to the benefit of PARCC, Inc., or any state of the Union
SBAC is a copyright of The Regents of the University of California – Smarter Balanced Assessment Consortium, which is not aff... Read More
SBAC is a copyright of The Regents of the University of California – Smarter Balanced Assessment Consortium, which is not affiliated to Lumos Learning. The Regents of the University of California – Smarter Balanced Assessment Consortium, was not involved in the production of, and does not endorse these products or this site.
ACT® Aspire™ is a registered trademark of ACT Aspire LLC., which is not affiliated to Lumos Learning. ACT Aspire LLC, was not... Read More
ACT® Aspire™ is a registered trademark of ACT Aspire LLC., which is not affiliated to Lumos Learning. ACT Aspire LLC,was not involved in the production of, and does not endorse these products or this site.
Florida Department of Education is not affiliated to Lumos Learning. Florida department of education, was not involved in the... Read More
Florida Department of Education is not affiliated to Lumos Learning. Florida department of education, was not involved in the production of, and does not endorse these products or this site.
Indiana Department of Education is not affiliated to Lumos Learning. Indiana department of education, was not involved in the... Read More
Indiana Department of Education is not affiliated to Lumos Learning. Indiana department of education, was not involved in the production of, and does not endorse these products or this site.
Mississippi Department of Education is not affiliated to Lumos Learning. Mississippi department of education, was not involved... Read More
Mississippi Department of Education is not affiliated to Lumos Learning. Mississippi department of education, was not involved in the production of, and does not endorse these products or this site.
Ohio Department of Education is not affiliated to Lumos Learning. Ohio department of education, was not involved in the prod... Read More
Ohio Department of Education is not affiliated to Lumos Learning. Ohio department of education, was not involved in the production of, and does not endorse these products or this site.
Tennessee Department of Education is not affiliated to Lumos Learning. Tennessee department of education, was not involved... Read More
Tennessee Department of Education is not affiliated to Lumos Learning. Tennessee department of education, was not involved in the production of, and does not endorse these products or this site.
Georgia Department of Education is not affiliated to Lumos Learning. Georgia department of education, was not involved... Read More
Georgia Department of Education is not affiliated to Lumos Learning. Georgia department of education, was not involved in the production of, and does not endorse these products or this site.
Missouri Department of Education is not affiliated to Lumos Learning. Missouri department of education, was not involved... Read More
Missouri Department of Education is not affiliated to Lumos Learning. Missouri department of education, was not involved in the production of, and does not endorse these products or this site.
Louisiana Department of Education is not affiliated to Lumos Learning. Louisiana department of education, was not involved... Read More
Louisiana Department of Education is not affiliated to Lumos Learning. Louisiana department of education, was not involved in the production of, and does not endorse these products or this site.
- Texas Go Math
- Big Ideas Math
- enVision Math
- EngageNY Math
- McGraw Hill My Math
- 180 Days of Math
- Math in Focus Answer Key
- Math Expressions Answer Key
- Privacy Policy

Texas Go Math Grade 7 Lesson 1.1 Answer Key Rational Numbers and Decimals
Refer to our Texas Go Math Grade 7 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 7 Lesson 1.1 Answer Key Rational Numbers and Decimals.
Texas Go Math Grade 7 Lesson 1.1 Answer Key Rational Numbers and Decimals
Texas Go Math Grade 7 Lesson 1.1 Explore Activity Answer Key

B. Now find the corresponding fraction of the decimal equivalents given in the last two columns in the table. Write the fractions in simplest form.
C. Conjecture What do you notice about the digits after the decimal point in the decimal forms of the fractions? Compare notes with your neighbor and refine your conjecture if necessary.
Question 1. Consider the decimal 0.101001000100001000001… Do you think this decimal represents a rational number? Why or why not? Answer: This decimal. number does not represent a rational number because it racks a repeating pattern.
Go Math Grade 7 Lesson 1.1 Rational Number Answers Question 2. Do you think a negative sign affects whether or not a number is a rational number? Use –\(\frac{8}{5}\) as an example. Answer: No, a negative sign does not affect whether or not a number is a rational number. – \(\frac{8}{5}\) = \(\frac{-8}{5}\) No, – \(\frac{8}{5}\) = \(\frac{-8}{5}\)
EXPLORE ACTIVITY (cont’d)
Question 3. Do you think a mixed number is a rational number? Explain. Answer: Yes, a mixed number is a rational number because it can be written as a simpLe fraction. For exampLe, 2 \(\frac{1}{4}\) = \(\frac{9}{4}\)
Write each rational number as a decimal.

Texas Go Math Grade 7 Lesson 1.1 Guided Practice Answer Key
Write each rational number as a decimal. Then tell whether each decimal is a terminating or a repeating decimal. (Explore Activity and Example 1)

Write each mixed number as a decimal. (Example 2)

Essential Question Check-In
Question 18. Tom is trying to write \(\frac{3}{47}\) as a decimal. He used long division and divided until he got the quotient 0.0638297872, at which point he stopped. Since the decimal doesn’t seem to terminate or repeat, he concluded that \(\frac{3}{47}\) is not rational. Do you agree or disagree? Why? Answer: Tom was wrong to conclude that \(\frac{3}{47}\) is not rational. First of all. \(\frac{3}{47}\) is a fraction. Thus, \(\frac{3}{47}\) is a rational number. After some time of long division, the patter would appear. I disagree. \(\frac{3}{47}\) is a rational number.
Texas Go Math Grade 7 Lesson 1.1 Independent Practice Answer Key

Go Math Grade 7 Lesson 1.1 Answer Key Grade 7 Question 25. Yvonne bought 4\(\frac{7}{8}\) yards of material to make a dress. a. What is 4\(\frac{7}{8}\) written as an improper fraction? Answer: 4 × 8 + 7 = 39 4\(\frac{7}{8}\) = \(\frac{39}{8}\)

c. Communicate Mathematical Ideas If Yvonne wanted to make 3 dresses that use 4\(\frac{7}{8}\) yd of fabric each, explain how she could use estimation to make sure she has enough fabric for all of them. Answer: Yvonne could multiply 4\(\frac{7}{8}\) by 3 and then buy some more yards (1 or 2) of fabric to ensure she would have enough to make 3 dresses.
Question 26. Vocabulary A rational number can be written as the ratio of one _________ to another and can be represented by a repeating or ________ decimal. Answer: A rational number can be written as the ratio of one integer to another and can be represented by a repeating or a terminating decimal.

Question 29. Analyze Relationships You are given a fraction in simplest form. The numerator is not zero. When you write the fraction as a decimal, it is a repeating decimal. Which numbers from 1 to 10 could be the denominator? Answer: The denominator could be a prime number (except 2 and 5) or a number that has a prime number in its factored form (again except 2 and 5). These numbers from 1 to 10 are: 3, 6 = 2 × 3, 7, 9 = 3 × 3
Question 30. Communicate Mathematical Ideas Julie got 21 of the 23 questions on her math test correct. She got 29 of the 32 questions on her science test correct. On which test did she get a higher score? Can you compare the fractions \(\frac{21}{23}\) and \(\frac{29}{32}\) by comparing 29 and 21 ? Explain. How can Julie compare her scores?. Answer: Divide the number of correct answers to the number of alt questions on both tests (round to 3 decimal digits). Compare those decimaL numbers to see on which test she scored better 21 ÷ 23 = 0.913 29 ÷ 32 = 0.906 0.913 > 0.906 She got a higher score on the first test. You can not compare those fractions by comparing 29 and 21 because the denominators are not equal. You could do that if they were equal.
Question 31. Look for a Pattern Look at the decimal 0.121122111222…. If the pattern continues, is this a repeating decimal? Explain. Answer: It is not a repeating decimal if the pattern continues This is not a repeating pattern. This pattern is created by adding 1 and 2 after 1 and 2 respectively. The pattern of a repeating decimal has to repeat without adding any other decimal in the pattern Example: 0.567567567… = \(0 . \overline{567}\) Is a repeating decimal. 0.56556555655556… IS NOT a repeating decimal because the pattern has an additional 5 at every repetition. This is not a repeating decimal if the pattern continues.
Share this:
Leave a comment cancel reply.
You must be logged in to post a comment.
- Texas Go Math
- Big Ideas Math
- Engageny Math
- McGraw Hill My Math
- enVision Math
- 180 Days of Math
- Math in Focus Answer Key
- Math Expressions Answer Key
- Privacy Policy
Into Math Grade 7 Module 1 Lesson 1 Answer Key Explore Relationships
We included H MH Into Math Grade 7 Answer Key PDF Module 1 Lesson 1 Explore Relationships to make students experts in learning maths.
HMH Into Math Grade 7 Module 1 Lesson 1 Answer Key Explore Relationships
I Can recognize when relationships presented in tables, diagrams, and verbal descriptions can be represented by a constant unit rate.
Spark Your Learning

On Fire! 2 tablespoons peppers; 5 tablespoons tomatoes
Blazin’ 4 tablespoons peppers; 12 tablespoons tomatoes
Kickin’ 6 tablespoons peppers; 15 tablespoons tomatoes
Feel the Burn 3 tablespoons peppers; 6 tablespoons tomatoes
If peppers and tomatoes are the only ingredients in the salsaš and the names are based on taste, which two salsas should have the same name? Show your work and explain.

Turn and Talk Using the ratios described in the salsa recipes, describe which recipe is most hot and which recipe is most mild.
Build Understanding

B. Describe a pattern you see in the columns of the table. _________________ _________________ Answer: The pattern in the column of the table is y = 8x Therefore x = 4 then y = 8(4) = 32 x = 8 then y = 8(8) = 64 x = 12 then y = 8(12) = 96 x = 16 then y= 8(16) = 128. x = 20 then y = 8(20) = 160.

D. You previously learned that a unit rate is a rate in which the second quantity in the comparison is one unit, such as 4 ounces per 1 serving. Describe the relationship between ounces of salsa and small jars of salsa using a unit rate. _________________ _________________ Answer: The relationship between ounces of salsa and small jars of salsa using a unit rate is 4 ounces = 1 serving y = 4x If x = 1 then y = 4 If x = 2 then y = 4(2) = 8 If x = 3 then y = 4(3) = 12 If x = 4 then y = 4(4) = 16 If x = 5 then y = 4(5) = 20

Turn and Talk Is the relationship represented in the table the same as the relationship represented in the diagram in Part E? Why or why not?

A. Can the relationship between the price and the number of avocados be described with a constant rate? Explain. ______________________ ______________________ Answer: The relationship between the price and the number of avocados is y = 1.25x If x = 1 then y = 1.25(1) = $1.25 If x = 2 then y = 1.25(2) = $2.50 If x = 3 then y = 1.25(3) = $3.75 If x = 4 then y = 1.25(4) = $5.00 If x = 5 then y = 1.25(5) = $6.25
B. Can the relationship between the weight and the number of avocados be described with a constant rate? Explain. ______________________ ______________________ ______________________
Check Understanding

On Your Own

For Problems 4-5, use the given information.
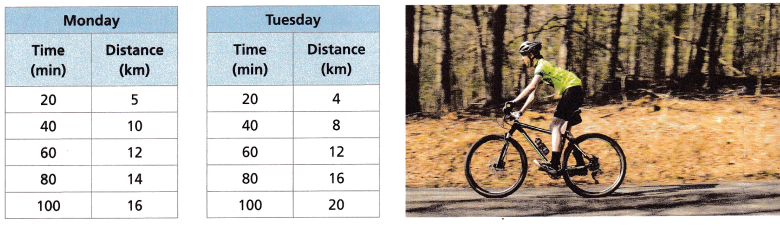
Question 4. Can the relationship in Monday’s table be described by a constant unit rate? Explain. ______________________ Answer: The rate between 20 and 40 min = (10 – 5)/(40 – 20) = 5/20 = 0.25 The rate between 40 and 60 min = (12 – 10)/(60 – 40) = 2/20 = 0.1 0.25 ≠ 0.10 Therefore the relationship in Monday’s table cannot be described by a constant unit rate.
Question 5. Can the relationship in Tuesday’s table be described by a constant unit rate? Explain. ______________________ Answer: The rate between 20 and 40 min = (8 – 4)/(40 – 20) = 4/20 = 0.2 The rate between 40 and 60 min = (12 – 8)/(60 – 40) = 4/20 = 0.2 0.2 = 0.2 Therefore the relationship in Monday’s table can be described by a constant unit rate.
I’m in a Learning Mindset!
What can I apply from previous work with ratios and rates to recognize when a relationship between two quantities can be described by a constant unit rate? _______________________ _______________________
Lesson 1.1 More Practice/Homework
Explore Relationships

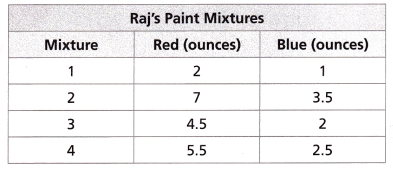
For Problems 4—5, use the values in the table.

Question 4. Can the relationship between cups of milk and cups of cereal be described by a constant ratio? Why or why not? Answer: Cups of cereal/ cups of milk = 12/4 = 3 and 18/6 = 3 So, the constant ratio is 1/3
Question 5. Can the relationship. between cups of cereal and servings of cereal be described by a constant rate? Why or why not? Answer: cups of cereal/ servings of cereal = 12/16 = 3/4 and 18/24 = 3/4 = 0.75 So, the rate is 0.75 or 3/4.
Question 6. Jane is saving to buy a cell phone. She is given a $100 gift to start and saves $35 a month from her allowance. So after 1 month, Jane has saved $135. Does it make sense to represent the relationship between the amount saved and the number of months with one constant rate? Why or why not? Explain your answer. Answer: Given, Jane is saving to buy a cell phone. She is given a $100 gift to start and saves $35 a month from her allowance. So after 1 month, Jane has saved $135 Let the number of months be x. Every month she saved $35 So, the relationship is 35x + 100.
Spiral Review
Question 8. At 1:00 p.m., a diver’s elevation is -30 feet relative to sea level. At 2:00 p.m., the diver’s elevation is -45 feet. At which time is the diver farther from sea level? Answer: Given, At 1:00 p.m., a diver’s elevation is -30 feet relative to sea level. tan 30° = P/B 1/√3 = P/B P1 = B/√3 At 2:00 p.m., the diver’s elevation is -45 feet. tan 45° = P/B 1= P2/B P2 = B So, at 2:00 pm, diver will be farther away from the sea level.
Question 9. A share of stock costs $83.60. The next day, the price increases $15.35. The following day, the price decreases $4.75. What is the final price? Answer: Given, A share of stock costs $83.60. The next day, the price increases $15.35. 83.60 + 15.35 = $98.95 The following day, the price decreases $4.75. $98.95 – $4.75 = $94.20 Hence the final price is $94.20
Leave a Comment Cancel Reply
You must be logged in to post a comment.

COMMENTS
Eureka Math Grade 1 Module 1 Lesson 27 Homework Answer Key. Use the number path to complete the number bond, and write an addition and a subtraction sentence to match. Question 1. a. b. Question 2. Solve the number sentences.
Here is a link to the pages I used for the homework. I used the "full module" PDF.https://www.engageny.org/resource/grade-1-mathematics-module-1
CPM Educational Program. With Mathleaks, you'll have instant access to expert solutions and answers to all of the CPM math questions you may have from the CPM Educational Program publications such as Pre-Algebra, Algebra 1, Algebra 2, and Geometry. Mathleaks offers the ultimate homework help and much of the content is free to use.
Answer Key. Chapter 1; Chapter 2; Chapter 3; Chapter 4; Chapter 5; Chapter 6; Chapter 7; Chapter 8; Chapter 9; Index; ... ⓐ 1 1 ⓑ 1 2 1 2 ... ⓑ 625 u 32 625 u 32 ⓒ −1 w 105 −1 w 105 ⓓ q 24 p 32 q 24 p 32 ⓔ 1 c 20 d 12 1 c 20 d 12; 9. ⓐ v 6 8 u 3 v 6 8 u 3 ⓑ 1 x 3 1 x 3 ⓒ e 4 f 4 e 4 f 4 ⓓ 27 r s 27 r s ⓔ 1 1
27. 7 28. 19 29. 2 30. 18 Side B 1. 0 2. 10 3. 1 4. 11 5. 0 6. 10 7. 1 8. 11 9. 3 10. 1 11. 11 12. 6 ... A STORY OF UNITS TEKS EDITION Lesson 8 Answer Key 1 • 3 208 Module 3: Ordering and Comparing Length Measurements as Numbers ... Homework 1. 1 2. 7 cm; 8 cm 3. 1 4. Model drawn; 11 + 4 = 15 or 15 − 11 = 4; 4 cm
Use Mathleaks to get learning-focused solutions and answers to Algebra 1 math, either 8th grade Algebra 1 or 9th grade Algebra 1, for the most commonly used textbooks from publishers such as Houghton Mifflin Harcourt, Big Ideas Learning, CPM, McGraw Hill, and Pearson. Getting helpful and educational math answers and solutions to high school ...
Translation Student Sheet—Answer Key Part I. Exploring Translations with Patty Paper 1. Move Points A, B, and C 2 units to the right. ORIGINAL COORDINATES ... (-1,-1) Observations: [Student answers will vary. Sample answer: You can subtract 5 to the x-coordinate and subtract 2
-2 -3 4 3 -1 1 4 9 6 4 3 or -3 9 12 25 30 16 12 144 10 21 60 31 -6 36 Rule: Double x and add 1 Rule: Halve x ... 15, 21, 27 ii. y=6x+3 c. 33 d. It will be a large "C," with width 101 and height 203. Horizontal parts will each ... Answer Key 17 Lesson 3.1.5 3-42. a. x-values between $10 and $100 are appropriate. b.
pc_1.1_packet.pdf: File Size: 296 kb: File Type: pdf: Download File. Units 1 & 2 packets are free! To purchase the entire course of lesson packets, click here. Practice Solutions. pc_1.1_practice_solutions.pdf: File Size: 347 kb: File Type: pdf: Download File. Application solutions are now available for purchase!
Answer: a 1 =9 and a i+1 =3a i for i≥1. Question 2. Answer the following questions about the recursive sequence generated by initial value, a 1 =4, and recurrence relation, a i+1 =4a i for i≥1. a. Find a formula for a 1, a 2, a 3, a 4, a 5 in terms of powers of 4. Answer: a 1 =4 1. a 2 =4 2.
Chapter 9 Homework Solutions - McLean County Unit 5 / Homepage
A typical Math Medic lesson always has the same four parts: Activity, Debrief Activity, QuickNotes, and Check Your Understanding. Here are the cliff notes: Activity:Students are in groups of 2 - 4 working collaboratively through the questions in the Activity. The teacher is checking in with groups and using questions, prompts, and cues to get ...
In the space below, describe the routine. STAYING SHARP 1.1 1. Solve the shape equation puzzle: If the large square represents one whole, what 3. fraction is represented by the shaded area? Answer with supporting work: Estimate, to the nearest dollar, the total cost: 5. $23.45 + $3.98 + $16.66 + $12.08 Answer with supporting work: 2.
Eureka Math Grade 1 Module 1 Lesson 25 Problem Set Answer Key. Break the total into parts. Write a number bond and addition and subtraction number sentences to match the story. Question 1. Rachel and Lucy are playing with 5 trucks. If Rachel is playing with 2 of them, how many is Lucy playing with? Lucy is playing with ______ trucks. Lucy is ...
Unit 1: Essentials of Geometry Lesson 1.1: Points, Lines, and Planes Objective Understand and use the basic undefined terms and defined terms in geometry such as point, line, plane, collinear, coplanar. USING UNDEFINED TERMS AND DEFINTIONS Point Name Example 1 Line Names Plane Names a. b. C. Name three points that are collinear: Name four ...
CPM Education Program proudly works to offer more and better math education to more students.
Answer Key Lesson 1.1 Practice Level C 1. @BA ... 27. 28. ray ray 29. 30. segment segment 31. 32. rays point 33. 34. 35. Created Date: 4/21/2006 7:06:17 PM ...
Georgia Milestones Assessment System Test Prep: Grade 3 English Language Arts Literacy (ELA) Practice Workbook and Full-length Online Assessments: GMAS Study Guide. Lumos Learning. 3. 2017. ACT Aspire Test Prep: 3rd Grade Math Practice Workbook and Full-length Online Assessments: ACT Aspire Study Guide. Lumos Learning.
Go Math Kindergarten Lesson 1.1 More Practice/Homework Question 4. Answer: Explanation: Count Two, traced Two with Two Counters in the five frame given shown. ... Go Math Kindergarten Chapter 1 Lesson 1.8 Answer Key Question 4. Answer: Explanation: ... => Number of Books Adam has = 1 - 1 = 0. Question 4. Answer:
Texas Go Math Grade 7 Lesson 1.1 Guided Practice Answer Key. Write each rational number as a decimal. Then tell whether each decimal is a terminating or a repeating decimal. (Explore Activity and Example 1) Question 1. [Math Processing Error] = ____________. Answer: Complete the long division.
Eureka Math Grade 1 Module 1 Lesson 37 Homework Answer Key. Make 5-group drawings and solve. Use the first number sentence to help you write a related number sentence that matches your picture. Question 1. Question 2. Question 3. Subtract. Then, write the related subtraction sentence. Make a math drawing if needed, and complete a number bond ...
We included HMH Into Math Grade 7 Answer Key PDF Module 1 Lesson 1 Explore Relationships to make students experts in learning maths.. HMH Into Math Grade 7 Module 1 Lesson 1 Answer Key Explore Relationships. I Can recognize when relationships presented in tables, diagrams, and verbal descriptions can be represented by a constant unit rate.