

Unraveling Research Population and Sample: Understanding their role in statistical inference
Research population and sample serve as the cornerstones of any scientific inquiry. They hold the power to unlock the mysteries hidden within data. Understanding the dynamics between the research population and sample is crucial for researchers. It ensures the validity, reliability, and generalizability of their findings. In this article, we uncover the profound role of the research population and sample, unveiling their differences and importance that reshapes our understanding of complex phenomena. Ultimately, this empowers researchers to make informed conclusions and drive meaningful advancements in our respective fields.
Table of Contents
What Is Population?
The research population, also known as the target population, refers to the entire group or set of individuals, objects, or events that possess specific characteristics and are of interest to the researcher. It represents the larger population from which a sample is drawn. The research population is defined based on the research objectives and the specific parameters or attributes under investigation. For example, in a study on the effects of a new drug, the research population would encompass all individuals who could potentially benefit from or be affected by the medication.
When Is Data Collection From a Population Preferred?
In certain scenarios where a comprehensive understanding of the entire group is required, it becomes necessary to collect data from a population. Here are a few situations when one prefers to collect data from a population:
1. Small or Accessible Population
When the research population is small or easily accessible, it may be feasible to collect data from the entire population. This is often the case in studies conducted within specific organizations, small communities, or well-defined groups where the population size is manageable.
2. Census or Complete Enumeration
In some cases, such as government surveys or official statistics, a census or complete enumeration of the population is necessary. This approach aims to gather data from every individual or entity within the population. This is typically done to ensure accurate representation and eliminate sampling errors.
3. Unique or Critical Characteristics
If the research focuses on a specific characteristic or trait that is rare and critical to the study, collecting data from the entire population may be necessary. This could be the case in studies related to rare diseases, endangered species, or specific genetic markers.
4. Legal or Regulatory Requirements
Certain legal or regulatory frameworks may require data collection from the entire population. For instance, government agencies might need comprehensive data on income levels, demographic characteristics, or healthcare utilization for policy-making or resource allocation purposes.
5. Precision or Accuracy Requirements
In situations where a high level of precision or accuracy is necessary, researchers may opt for population-level data collection. By doing so, they mitigate the potential for sampling error and obtain more reliable estimates of population parameters.
What Is a Sample?
A sample is a subset of the research population that is carefully selected to represent its characteristics. Researchers study this smaller, manageable group to draw inferences that they can generalize to the larger population. The selection of the sample must be conducted in a manner that ensures it accurately reflects the diversity and pertinent attributes of the research population. By studying a sample, researchers can gather data more efficiently and cost-effectively compared to studying the entire population. The findings from the sample are then extrapolated to make conclusions about the larger research population.
What Is Sampling and Why Is It Important?
Sampling refers to the process of selecting a sample from a larger group or population of interest in order to gather data and make inferences. The goal of sampling is to obtain a sample that is representative of the population, meaning that the sample accurately reflects the key attributes, variations, and proportions present in the population. By studying the sample, researchers can draw conclusions or make predictions about the larger population with a certain level of confidence.
Collecting data from a sample, rather than the entire population, offers several advantages and is often necessary due to practical constraints. Here are some reasons to collect data from a sample:
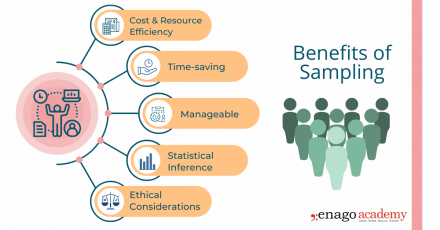
1. Cost and Resource Efficiency
Collecting data from an entire population can be expensive and time-consuming. Sampling allows researchers to gather information from a smaller subset of the population, reducing costs and resource requirements. It is often more practical and feasible to collect data from a sample, especially when the population size is large or geographically dispersed.
2. Time Constraints
Conducting research with a sample allows for quicker data collection and analysis compared to studying the entire population. It saves time by focusing efforts on a smaller group, enabling researchers to obtain results more efficiently. This is particularly beneficial in time-sensitive research projects or situations that necessitate prompt decision-making.
3. Manageable Data Collection
Working with a sample makes data collection more manageable . Researchers can concentrate their efforts on a smaller group, allowing for more detailed and thorough data collection methods. Furthermore, it is more convenient and reliable to store and conduct statistical analyses on smaller datasets. This also facilitates in-depth insights and a more comprehensive understanding of the research topic.
4. Statistical Inference
Collecting data from a well-selected and representative sample enables valid statistical inference. By using appropriate statistical techniques, researchers can generalize the findings from the sample to the larger population. This allows for meaningful inferences, predictions, and estimation of population parameters, thus providing insights beyond the specific individuals or elements in the sample.
5. Ethical Considerations
In certain cases, collecting data from an entire population may pose ethical challenges, such as invasion of privacy or burdening participants. Sampling helps protect the privacy and well-being of individuals by reducing the burden of data collection. It allows researchers to obtain valuable information while ensuring ethical standards are maintained .
Key Steps Involved in the Sampling Process
Sampling is a valuable tool in research; however, it is important to carefully consider the sampling method, sample size, and potential biases to ensure that the findings accurately represent the larger population and are valid for making conclusions and generalizations. While the specific steps may vary depending on the research context, here is a general outline of the sampling process:
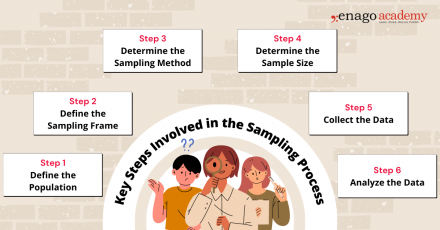
1. Define the Population
Clearly define the target population for your research study. The population should encompass the group of individuals, elements, or units that you want to draw conclusions about.
2. Define the Sampling Frame
Create a sampling frame, which is a list or representation of the individuals or elements in the target population. The sampling frame should be comprehensive and accurately reflect the population you want to study.
3. Determine the Sampling Method
Select an appropriate sampling method based on your research objectives, available resources, and the characteristics of the population. You can perform sampling by either utilizing probability-based or non-probability-based techniques. Common sampling methods include random sampling, stratified sampling, cluster sampling, and convenience sampling.
4. Determine Sample Size
Determine the desired sample size based on statistical considerations, such as the level of precision required, desired confidence level, and expected variability within the population. Larger sample sizes generally reduce sampling error but may be constrained by practical limitations.
5. Collect Data
Once the sample is selected using the appropriate technique, collect the necessary data according to the research design and data collection methods . Ensure that you use standardized and consistent data collection process that is also appropriate for your research objectives.
6. Analyze the Data
Perform the necessary statistical analyses on the collected data to derive meaningful insights. Use appropriate statistical techniques to make inferences, estimate population parameters, test hypotheses, or identify patterns and relationships within the data.
Population vs Sample — Differences and examples
While the population provides a comprehensive overview of the entire group under study, the sample, on the other hand, allows researchers to draw inferences and make generalizations about the population. Researchers should employ careful sampling techniques to ensure that the sample is representative and accurately reflects the characteristics and variability of the population.

Research Study: Investigating the prevalence of stress among high school students in a specific city and its impact on academic performance.
Population: All high school students in a particular city
Sampling Frame: The sampling frame would involve obtaining a comprehensive list of all high schools in the specific city. A random selection of schools would be made from this list to ensure representation from different areas and demographics of the city.
Sample: Randomly selected 500 high school students from different schools in the city
The sample represents a subset of the entire population of high school students in the city.
Research Study: Assessing the effectiveness of a new medication in managing symptoms and improving quality of life in patients with the specific medical condition.
Population: Patients diagnosed with a specific medical condition
Sampling Frame: The sampling frame for this study would involve accessing medical records or databases that include information on patients diagnosed with the specific medical condition. Researchers would select a convenient sample of patients who meet the inclusion criteria from the sampling frame.
Sample: Convenient sample of 100 patients from a local clinic who meet the inclusion criteria for the study
The sample consists of patients from the larger population of individuals diagnosed with the medical condition.
Research Study: Investigating community perceptions of safety and satisfaction with local amenities in the neighborhood.
Population: Residents of a specific neighborhood
Sampling Frame: The sampling frame for this study would involve obtaining a list of residential addresses within the specific neighborhood. Various sources such as census data, voter registration records, or community databases offer the means to obtain this information. From the sampling frame, researchers would randomly select a cluster sample of households to ensure representation from different areas within the neighborhood.
Sample: Cluster sample of 50 households randomly selected from different blocks within the neighborhood
The sample represents a subset of the entire population of residents living in the neighborhood.
To summarize, sampling allows for cost-effective data collection, easier statistical analysis, and increased practicality compared to studying the entire population. However, despite these advantages, sampling is subject to various challenges. These challenges include sampling bias, non-response bias, and the potential for sampling errors.
To minimize bias and enhance the validity of research findings , researchers should employ appropriate sampling techniques, clearly define the population, establish a comprehensive sampling frame, and monitor the sampling process for potential biases. Validating findings by comparing them to known population characteristics can also help evaluate the generalizability of the results. Properly understanding and implementing sampling techniques ensure that research findings are accurate, reliable, and representative of the larger population. By carefully considering the choice of population and sample, researchers can draw meaningful conclusions and, consequently, make valuable contributions to their respective fields of study.
Now, it’s your turn! Take a moment to think about a research question that interests you. Consider the population that would be relevant to your inquiry. Who would you include in your sample? How would you go about selecting them? Reflecting on these aspects will help you appreciate the intricacies involved in designing a research study. Let us know about it in the comment section below or reach out to us using #AskEnago and tag @EnagoAcademy on Twitter , Facebook , and Quora .
Thank you very much, this is helpful
Very impressive and helpful and also easy to understand….. Thanks to the Author and Publisher….
Rate this article Cancel Reply
Your email address will not be published.

Enago Academy's Most Popular Articles

- Publishing Research
- Trending Now
- Understanding Ethics
Understanding the Impact of Retractions on Research Integrity – A global study
As we reach the midway point of 2024, ‘Research Integrity’ remains one of the hot…

- Diversity and Inclusion
The Silent Struggle: Confronting gender bias in science funding
In the 1990s, Dr. Katalin Kariko’s pioneering mRNA research seemed destined for obscurity, doomed by…

- Reporting Research
Choosing the Right Analytical Approach: Thematic analysis vs. content analysis for data interpretation
In research, choosing the right approach to understand data is crucial for deriving meaningful insights.…

Addressing Barriers in Academia: Navigating unconscious biases in the Ph.D. journey
In the journey of academia, a Ph.D. marks a transitional phase, like that of a…

Comparing Cross Sectional and Longitudinal Studies: 5 steps for choosing the right approach
The process of choosing the right research design can put ourselves at the crossroads of…
Choosing the Right Analytical Approach: Thematic analysis vs. content analysis for…
Comparing Cross Sectional and Longitudinal Studies: 5 steps for choosing the right…

Sign-up to read more
Subscribe for free to get unrestricted access to all our resources on research writing and academic publishing including:
- 2000+ blog articles
- 50+ Webinars
- 10+ Expert podcasts
- 50+ Infographics
- 10+ Checklists
- Research Guides
We hate spam too. We promise to protect your privacy and never spam you.

Sampling Methods & Strategies 101
Everything you need to know (including examples)
By: Derek Jansen (MBA) | Expert Reviewed By: Kerryn Warren (PhD) | January 2023
If you’re new to research, sooner or later you’re bound to wander into the intimidating world of sampling methods and strategies. If you find yourself on this page, chances are you’re feeling a little overwhelmed or confused. Fear not – in this post we’ll unpack sampling in straightforward language , along with loads of examples .
Overview: Sampling Methods & Strategies
- What is sampling in a research context?
- The two overarching approaches
Simple random sampling
Stratified random sampling, cluster sampling, systematic sampling, purposive sampling, convenience sampling, snowball sampling.
- How to choose the right sampling method
What (exactly) is sampling?
At the simplest level, sampling (within a research context) is the process of selecting a subset of participants from a larger group . For example, if your research involved assessing US consumers’ perceptions about a particular brand of laundry detergent, you wouldn’t be able to collect data from every single person that uses laundry detergent (good luck with that!) – but you could potentially collect data from a smaller subset of this group.
In technical terms, the larger group is referred to as the population , and the subset (the group you’ll actually engage with in your research) is called the sample . Put another way, you can look at the population as a full cake and the sample as a single slice of that cake. In an ideal world, you’d want your sample to be perfectly representative of the population, as that would allow you to generalise your findings to the entire population. In other words, you’d want to cut a perfect cross-sectional slice of cake, such that the slice reflects every layer of the cake in perfect proportion.
Achieving a truly representative sample is, unfortunately, a little trickier than slicing a cake, as there are many practical challenges and obstacles to achieving this in a real-world setting. Thankfully though, you don’t always need to have a perfectly representative sample – it all depends on the specific research aims of each study – so don’t stress yourself out about that just yet!
With the concept of sampling broadly defined, let’s look at the different approaches to sampling to get a better understanding of what it all looks like in practice.

The two overarching sampling approaches
At the highest level, there are two approaches to sampling: probability sampling and non-probability sampling . Within each of these, there are a variety of sampling methods , which we’ll explore a little later.
Probability sampling involves selecting participants (or any unit of interest) on a statistically random basis , which is why it’s also called “random sampling”. In other words, the selection of each individual participant is based on a pre-determined process (not the discretion of the researcher). As a result, this approach achieves a random sample.
Probability-based sampling methods are most commonly used in quantitative research , especially when it’s important to achieve a representative sample that allows the researcher to generalise their findings.
Non-probability sampling , on the other hand, refers to sampling methods in which the selection of participants is not statistically random . In other words, the selection of individual participants is based on the discretion and judgment of the researcher, rather than on a pre-determined process.
Non-probability sampling methods are commonly used in qualitative research , where the richness and depth of the data are more important than the generalisability of the findings.
If that all sounds a little too conceptual and fluffy, don’t worry. Let’s take a look at some actual sampling methods to make it more tangible.
Need a helping hand?
Probability-based sampling methods
First, we’ll look at four common probability-based (random) sampling methods:
Importantly, this is not a comprehensive list of all the probability sampling methods – these are just four of the most common ones. So, if you’re interested in adopting a probability-based sampling approach, be sure to explore all the options.
Simple random sampling involves selecting participants in a completely random fashion , where each participant has an equal chance of being selected. Basically, this sampling method is the equivalent of pulling names out of a hat , except that you can do it digitally. For example, if you had a list of 500 people, you could use a random number generator to draw a list of 50 numbers (each number, reflecting a participant) and then use that dataset as your sample.
Thanks to its simplicity, simple random sampling is easy to implement , and as a consequence, is typically quite cheap and efficient . Given that the selection process is completely random, the results can be generalised fairly reliably. However, this also means it can hide the impact of large subgroups within the data, which can result in minority subgroups having little representation in the results – if any at all. To address this, one needs to take a slightly different approach, which we’ll look at next.
Stratified random sampling is similar to simple random sampling, but it kicks things up a notch. As the name suggests, stratified sampling involves selecting participants randomly , but from within certain pre-defined subgroups (i.e., strata) that share a common trait . For example, you might divide the population into strata based on gender, ethnicity, age range or level of education, and then select randomly from each group.
The benefit of this sampling method is that it gives you more control over the impact of large subgroups (strata) within the population. For example, if a population comprises 80% males and 20% females, you may want to “balance” this skew out by selecting a random sample from an equal number of males and females. This would, of course, reduce the representativeness of the sample, but it would allow you to identify differences between subgroups. So, depending on your research aims, the stratified approach could work well.

Next on the list is cluster sampling. As the name suggests, this sampling method involves sampling from naturally occurring, mutually exclusive clusters within a population – for example, area codes within a city or cities within a country. Once the clusters are defined, a set of clusters are randomly selected and then a set of participants are randomly selected from each cluster.
Now, you’re probably wondering, “how is cluster sampling different from stratified random sampling?”. Well, let’s look at the previous example where each cluster reflects an area code in a given city.
With cluster sampling, you would collect data from clusters of participants in a handful of area codes (let’s say 5 neighbourhoods). Conversely, with stratified random sampling, you would need to collect data from all over the city (i.e., many more neighbourhoods). You’d still achieve the same sample size either way (let’s say 200 people, for example), but with stratified sampling, you’d need to do a lot more running around, as participants would be scattered across a vast geographic area. As a result, cluster sampling is often the more practical and economical option.
If that all sounds a little mind-bending, you can use the following general rule of thumb. If a population is relatively homogeneous , cluster sampling will often be adequate. Conversely, if a population is quite heterogeneous (i.e., diverse), stratified sampling will generally be more appropriate.
The last probability sampling method we’ll look at is systematic sampling. This method simply involves selecting participants at a set interval , starting from a random point .
For example, if you have a list of students that reflects the population of a university, you could systematically sample that population by selecting participants at an interval of 8 . In other words, you would randomly select a starting point – let’s say student number 40 – followed by student 48, 56, 64, etc.
What’s important with systematic sampling is that the population list you select from needs to be randomly ordered . If there are underlying patterns in the list (for example, if the list is ordered by gender, IQ, age, etc.), this will result in a non-random sample, which would defeat the purpose of adopting this sampling method. Of course, you could safeguard against this by “shuffling” your population list using a random number generator or similar tool.

Non-probability-based sampling methods
Right, now that we’ve looked at a few probability-based sampling methods, let’s look at three non-probability methods :
Again, this is not an exhaustive list of all possible sampling methods, so be sure to explore further if you’re interested in adopting a non-probability sampling approach.
First up, we’ve got purposive sampling – also known as judgment , selective or subjective sampling. Again, the name provides some clues, as this method involves the researcher selecting participants using his or her own judgement , based on the purpose of the study (i.e., the research aims).
For example, suppose your research aims were to understand the perceptions of hyper-loyal customers of a particular retail store. In that case, you could use your judgement to engage with frequent shoppers, as well as rare or occasional shoppers, to understand what judgements drive the two behavioural extremes .
Purposive sampling is often used in studies where the aim is to gather information from a small population (especially rare or hard-to-find populations), as it allows the researcher to target specific individuals who have unique knowledge or experience . Naturally, this sampling method is quite prone to researcher bias and judgement error, and it’s unlikely to produce generalisable results, so it’s best suited to studies where the aim is to go deep rather than broad .

Next up, we have convenience sampling. As the name suggests, with this method, participants are selected based on their availability or accessibility . In other words, the sample is selected based on how convenient it is for the researcher to access it, as opposed to using a defined and objective process.
Naturally, convenience sampling provides a quick and easy way to gather data, as the sample is selected based on the individuals who are readily available or willing to participate. This makes it an attractive option if you’re particularly tight on resources and/or time. However, as you’d expect, this sampling method is unlikely to produce a representative sample and will of course be vulnerable to researcher bias , so it’s important to approach it with caution.
Last but not least, we have the snowball sampling method. This method relies on referrals from initial participants to recruit additional participants. In other words, the initial subjects form the first (small) snowball and each additional subject recruited through referral is added to the snowball, making it larger as it rolls along .
Snowball sampling is often used in research contexts where it’s difficult to identify and access a particular population. For example, people with a rare medical condition or members of an exclusive group. It can also be useful in cases where the research topic is sensitive or taboo and people are unlikely to open up unless they’re referred by someone they trust.
Simply put, snowball sampling is ideal for research that involves reaching hard-to-access populations . But, keep in mind that, once again, it’s a sampling method that’s highly prone to researcher bias and is unlikely to produce a representative sample. So, make sure that it aligns with your research aims and questions before adopting this method.
How to choose a sampling method
Now that we’ve looked at a few popular sampling methods (both probability and non-probability based), the obvious question is, “ how do I choose the right sampling method for my study?”. When selecting a sampling method for your research project, you’ll need to consider two important factors: your research aims and your resources .
As with all research design and methodology choices, your sampling approach needs to be guided by and aligned with your research aims, objectives and research questions – in other words, your golden thread. Specifically, you need to consider whether your research aims are primarily concerned with producing generalisable findings (in which case, you’ll likely opt for a probability-based sampling method) or with achieving rich , deep insights (in which case, a non-probability-based approach could be more practical). Typically, quantitative studies lean toward the former, while qualitative studies aim for the latter, so be sure to consider your broader methodology as well.
The second factor you need to consider is your resources and, more generally, the practical constraints at play. If, for example, you have easy, free access to a large sample at your workplace or university and a healthy budget to help you attract participants, that will open up multiple options in terms of sampling methods. Conversely, if you’re cash-strapped, short on time and don’t have unfettered access to your population of interest, you may be restricted to convenience or referral-based methods.
In short, be ready for trade-offs – you won’t always be able to utilise the “perfect” sampling method for your study, and that’s okay. Much like all the other methodological choices you’ll make as part of your study, you’ll often need to compromise and accept practical trade-offs when it comes to sampling. Don’t let this get you down though – as long as your sampling choice is well explained and justified, and the limitations of your approach are clearly articulated, you’ll be on the right track.

Let’s recap…
In this post, we’ve covered the basics of sampling within the context of a typical research project.
- Sampling refers to the process of defining a subgroup (sample) from the larger group of interest (population).
- The two overarching approaches to sampling are probability sampling (random) and non-probability sampling .
- Common probability-based sampling methods include simple random sampling, stratified random sampling, cluster sampling and systematic sampling.
- Common non-probability-based sampling methods include purposive sampling, convenience sampling and snowball sampling.
- When choosing a sampling method, you need to consider your research aims , objectives and questions, as well as your resources and other practical constraints .
If you’d like to see an example of a sampling strategy in action, be sure to check out our research methodology chapter sample .
Last but not least, if you need hands-on help with your sampling (or any other aspect of your research), take a look at our 1-on-1 coaching service , where we guide you through each step of the research process, at your own pace.

Psst... there’s more!
This post was based on one of our popular Research Bootcamps . If you're working on a research project, you'll definitely want to check this out ...
Excellent and helpful. Best site to get a full understanding of Research methodology. I’m nolonger as “clueless “..😉
Excellent and helpful for junior researcher!
Grad Coach tutorials are excellent – I recommend them to everyone doing research. I will be working with a sample of imprisoned women and now have a much clearer idea concerning sampling. Thank you to all at Grad Coach for generously sharing your expertise with students.
Submit a Comment Cancel reply
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
- Print Friendly
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, automatically generate references for free.
- Knowledge Base
- Methodology
Research Design | Step-by-Step Guide with Examples
Published on 5 May 2022 by Shona McCombes . Revised on 20 March 2023.
A research design is a strategy for answering your research question using empirical data. Creating a research design means making decisions about:
- Your overall aims and approach
- The type of research design you’ll use
- Your sampling methods or criteria for selecting subjects
- Your data collection methods
- The procedures you’ll follow to collect data
- Your data analysis methods
A well-planned research design helps ensure that your methods match your research aims and that you use the right kind of analysis for your data.
Table of contents
Step 1: consider your aims and approach, step 2: choose a type of research design, step 3: identify your population and sampling method, step 4: choose your data collection methods, step 5: plan your data collection procedures, step 6: decide on your data analysis strategies, frequently asked questions.
- Introduction
Before you can start designing your research, you should already have a clear idea of the research question you want to investigate.
There are many different ways you could go about answering this question. Your research design choices should be driven by your aims and priorities – start by thinking carefully about what you want to achieve.
The first choice you need to make is whether you’ll take a qualitative or quantitative approach.
| Qualitative approach | Quantitative approach |
|---|---|
Qualitative research designs tend to be more flexible and inductive , allowing you to adjust your approach based on what you find throughout the research process.
Quantitative research designs tend to be more fixed and deductive , with variables and hypotheses clearly defined in advance of data collection.
It’s also possible to use a mixed methods design that integrates aspects of both approaches. By combining qualitative and quantitative insights, you can gain a more complete picture of the problem you’re studying and strengthen the credibility of your conclusions.
Practical and ethical considerations when designing research
As well as scientific considerations, you need to think practically when designing your research. If your research involves people or animals, you also need to consider research ethics .
- How much time do you have to collect data and write up the research?
- Will you be able to gain access to the data you need (e.g., by travelling to a specific location or contacting specific people)?
- Do you have the necessary research skills (e.g., statistical analysis or interview techniques)?
- Will you need ethical approval ?
At each stage of the research design process, make sure that your choices are practically feasible.
Prevent plagiarism, run a free check.
Within both qualitative and quantitative approaches, there are several types of research design to choose from. Each type provides a framework for the overall shape of your research.
Types of quantitative research designs
Quantitative designs can be split into four main types. Experimental and quasi-experimental designs allow you to test cause-and-effect relationships, while descriptive and correlational designs allow you to measure variables and describe relationships between them.
| Type of design | Purpose and characteristics |
|---|---|
| Experimental | |
| Quasi-experimental | |
| Correlational | |
| Descriptive |
With descriptive and correlational designs, you can get a clear picture of characteristics, trends, and relationships as they exist in the real world. However, you can’t draw conclusions about cause and effect (because correlation doesn’t imply causation ).
Experiments are the strongest way to test cause-and-effect relationships without the risk of other variables influencing the results. However, their controlled conditions may not always reflect how things work in the real world. They’re often also more difficult and expensive to implement.
Types of qualitative research designs
Qualitative designs are less strictly defined. This approach is about gaining a rich, detailed understanding of a specific context or phenomenon, and you can often be more creative and flexible in designing your research.
The table below shows some common types of qualitative design. They often have similar approaches in terms of data collection, but focus on different aspects when analysing the data.
| Type of design | Purpose and characteristics |
|---|---|
| Grounded theory | |
| Phenomenology |
Your research design should clearly define who or what your research will focus on, and how you’ll go about choosing your participants or subjects.
In research, a population is the entire group that you want to draw conclusions about, while a sample is the smaller group of individuals you’ll actually collect data from.
Defining the population
A population can be made up of anything you want to study – plants, animals, organisations, texts, countries, etc. In the social sciences, it most often refers to a group of people.
For example, will you focus on people from a specific demographic, region, or background? Are you interested in people with a certain job or medical condition, or users of a particular product?
The more precisely you define your population, the easier it will be to gather a representative sample.
Sampling methods
Even with a narrowly defined population, it’s rarely possible to collect data from every individual. Instead, you’ll collect data from a sample.
To select a sample, there are two main approaches: probability sampling and non-probability sampling . The sampling method you use affects how confidently you can generalise your results to the population as a whole.
| Probability sampling | Non-probability sampling |
|---|---|
Probability sampling is the most statistically valid option, but it’s often difficult to achieve unless you’re dealing with a very small and accessible population.
For practical reasons, many studies use non-probability sampling, but it’s important to be aware of the limitations and carefully consider potential biases. You should always make an effort to gather a sample that’s as representative as possible of the population.
Case selection in qualitative research
In some types of qualitative designs, sampling may not be relevant.
For example, in an ethnography or a case study, your aim is to deeply understand a specific context, not to generalise to a population. Instead of sampling, you may simply aim to collect as much data as possible about the context you are studying.
In these types of design, you still have to carefully consider your choice of case or community. You should have a clear rationale for why this particular case is suitable for answering your research question.
For example, you might choose a case study that reveals an unusual or neglected aspect of your research problem, or you might choose several very similar or very different cases in order to compare them.
Data collection methods are ways of directly measuring variables and gathering information. They allow you to gain first-hand knowledge and original insights into your research problem.
You can choose just one data collection method, or use several methods in the same study.
Survey methods
Surveys allow you to collect data about opinions, behaviours, experiences, and characteristics by asking people directly. There are two main survey methods to choose from: questionnaires and interviews.
| Questionnaires | Interviews |
|---|---|
Observation methods
Observations allow you to collect data unobtrusively, observing characteristics, behaviours, or social interactions without relying on self-reporting.
Observations may be conducted in real time, taking notes as you observe, or you might make audiovisual recordings for later analysis. They can be qualitative or quantitative.
| Quantitative observation | |
|---|---|
Other methods of data collection
There are many other ways you might collect data depending on your field and topic.
| Field | Examples of data collection methods |
|---|---|
| Media & communication | Collecting a sample of texts (e.g., speeches, articles, or social media posts) for data on cultural norms and narratives |
| Psychology | Using technologies like neuroimaging, eye-tracking, or computer-based tasks to collect data on things like attention, emotional response, or reaction time |
| Education | Using tests or assignments to collect data on knowledge and skills |
| Physical sciences | Using scientific instruments to collect data on things like weight, blood pressure, or chemical composition |
If you’re not sure which methods will work best for your research design, try reading some papers in your field to see what data collection methods they used.
Secondary data
If you don’t have the time or resources to collect data from the population you’re interested in, you can also choose to use secondary data that other researchers already collected – for example, datasets from government surveys or previous studies on your topic.
With this raw data, you can do your own analysis to answer new research questions that weren’t addressed by the original study.
Using secondary data can expand the scope of your research, as you may be able to access much larger and more varied samples than you could collect yourself.
However, it also means you don’t have any control over which variables to measure or how to measure them, so the conclusions you can draw may be limited.
As well as deciding on your methods, you need to plan exactly how you’ll use these methods to collect data that’s consistent, accurate, and unbiased.
Planning systematic procedures is especially important in quantitative research, where you need to precisely define your variables and ensure your measurements are reliable and valid.
Operationalisation
Some variables, like height or age, are easily measured. But often you’ll be dealing with more abstract concepts, like satisfaction, anxiety, or competence. Operationalisation means turning these fuzzy ideas into measurable indicators.
If you’re using observations , which events or actions will you count?
If you’re using surveys , which questions will you ask and what range of responses will be offered?
You may also choose to use or adapt existing materials designed to measure the concept you’re interested in – for example, questionnaires or inventories whose reliability and validity has already been established.
Reliability and validity
Reliability means your results can be consistently reproduced , while validity means that you’re actually measuring the concept you’re interested in.
| Reliability | Validity |
|---|---|
For valid and reliable results, your measurement materials should be thoroughly researched and carefully designed. Plan your procedures to make sure you carry out the same steps in the same way for each participant.
If you’re developing a new questionnaire or other instrument to measure a specific concept, running a pilot study allows you to check its validity and reliability in advance.
Sampling procedures
As well as choosing an appropriate sampling method, you need a concrete plan for how you’ll actually contact and recruit your selected sample.
That means making decisions about things like:
- How many participants do you need for an adequate sample size?
- What inclusion and exclusion criteria will you use to identify eligible participants?
- How will you contact your sample – by mail, online, by phone, or in person?
If you’re using a probability sampling method, it’s important that everyone who is randomly selected actually participates in the study. How will you ensure a high response rate?
If you’re using a non-probability method, how will you avoid bias and ensure a representative sample?
Data management
It’s also important to create a data management plan for organising and storing your data.
Will you need to transcribe interviews or perform data entry for observations? You should anonymise and safeguard any sensitive data, and make sure it’s backed up regularly.
Keeping your data well organised will save time when it comes to analysing them. It can also help other researchers validate and add to your findings.
On their own, raw data can’t answer your research question. The last step of designing your research is planning how you’ll analyse the data.
Quantitative data analysis
In quantitative research, you’ll most likely use some form of statistical analysis . With statistics, you can summarise your sample data, make estimates, and test hypotheses.
Using descriptive statistics , you can summarise your sample data in terms of:
- The distribution of the data (e.g., the frequency of each score on a test)
- The central tendency of the data (e.g., the mean to describe the average score)
- The variability of the data (e.g., the standard deviation to describe how spread out the scores are)
The specific calculations you can do depend on the level of measurement of your variables.
Using inferential statistics , you can:
- Make estimates about the population based on your sample data.
- Test hypotheses about a relationship between variables.
Regression and correlation tests look for associations between two or more variables, while comparison tests (such as t tests and ANOVAs ) look for differences in the outcomes of different groups.
Your choice of statistical test depends on various aspects of your research design, including the types of variables you’re dealing with and the distribution of your data.
Qualitative data analysis
In qualitative research, your data will usually be very dense with information and ideas. Instead of summing it up in numbers, you’ll need to comb through the data in detail, interpret its meanings, identify patterns, and extract the parts that are most relevant to your research question.
Two of the most common approaches to doing this are thematic analysis and discourse analysis .
| Approach | Characteristics |
|---|---|
| Thematic analysis | |
| Discourse analysis |
There are many other ways of analysing qualitative data depending on the aims of your research. To get a sense of potential approaches, try reading some qualitative research papers in your field.
A sample is a subset of individuals from a larger population. Sampling means selecting the group that you will actually collect data from in your research.
For example, if you are researching the opinions of students in your university, you could survey a sample of 100 students.
Statistical sampling allows you to test a hypothesis about the characteristics of a population. There are various sampling methods you can use to ensure that your sample is representative of the population as a whole.
Operationalisation means turning abstract conceptual ideas into measurable observations.
For example, the concept of social anxiety isn’t directly observable, but it can be operationally defined in terms of self-rating scores, behavioural avoidance of crowded places, or physical anxiety symptoms in social situations.
Before collecting data , it’s important to consider how you will operationalise the variables that you want to measure.
The research methods you use depend on the type of data you need to answer your research question .
- If you want to measure something or test a hypothesis , use quantitative methods . If you want to explore ideas, thoughts, and meanings, use qualitative methods .
- If you want to analyse a large amount of readily available data, use secondary data. If you want data specific to your purposes with control over how they are generated, collect primary data.
- If you want to establish cause-and-effect relationships between variables , use experimental methods. If you want to understand the characteristics of a research subject, use descriptive methods.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.
McCombes, S. (2023, March 20). Research Design | Step-by-Step Guide with Examples. Scribbr. Retrieved 10 July 2024, from https://www.scribbr.co.uk/research-methods/research-design/
Is this article helpful?
Shona McCombes
Introduction to Research Methods
7 samples and populations.
So you’ve developed your research question, figured out how you’re going to measure whatever you want to study, and have your survey or interviews ready to go. Now all your need is other people to become your data.
You might say ‘easy!’, there’s people all around you. You have a big family tree and surely them and their friends would have happy to take your survey. And then there’s your friends and people you’re in class with. Finding people is way easier than writing the interview questions or developing the survey. That reaction might be a strawman, maybe you’ve come to the conclusion none of this is easy. For your data to be valuable, you not only have to ask the right questions, you have to ask the right people. The “right people” aren’t the best or the smartest people, the right people are driven by what your study is trying to answer and the method you’re using to answer it.
Remember way back in chapter 2 when we looked at this chart and discussed the differences between qualitative and quantitative data.
| Qualitative | Quantitative | |
|---|---|---|
| Purpose | Understanding underlying motivations or reasons; depth of knowledge | Generalize results to the population; make predictions |
| Sample | Small and narrow; not generally representative | Large and broad |
| Method | Interviews, focus groups, case studies | Surveys, web scrapping |
| Analysis | Interpretative, content analysis | Statistical, numeric |
One of the biggest differences between quantitative and qualitative data was whether we wanted to be able to explain something for a lot of people (what percentage of residents in Oklahoma support legalizing marijuana?) versus explaining the reasons for those opinions (why do some people support legalizing marijuana and others not?). The underlying differences there is whether our goal is explain something about everyone, or whether we’re content to explain it about just our respondents.
‘Everyone’ is called the population . The population in research is whatever group the research is trying to answer questions about. The population could be everyone on planet Earth, everyone in the United States, everyone in rural counties of Iowa, everyone at your university, and on and on. It is simply everyone within the unit you are intending to study.
In order to study the population, we typically take a sample or a subset. A sample is simply a smaller number of people from the population that are studied, which we can use to then understand the characteristics of the population based on that subset. That’s why a poll of 1300 likely voters can be used to guess at who will win your states Governor race. It isn’t perfect, and we’ll talk about the math behind all of it in a later chapter, but for now we’ll just focus on the different types of samples you might use to study a population with a survey.
If correctly sampled, we can use the sample to generalize information we get to the population. Generalizability , which we defined earlier, means we can assume the responses of people to our study match the responses everyone would have given us. We can only do that if the sample is representative of the population, meaning that they are alike on important characteristics such as race, gender, age, education. If something makes a large difference in people’s views on a topic in your research and your sample is not balanced, you’ll get inaccurate results.
Generalizability is more of a concern with surveys than with interviews. The goal of a survey is to explain something about people beyond the sample you get responses from. You’ll never see a news headline saying that “53% of 1250 Americans that responded to a poll approve of the President”. It’s only worth asking those 1250 people if we can assume the rest of the United States feels the same way overall. With interviews though we’re looking for depth from their responses, and so we are less hopefully that the 15 people we talk to will exactly match the American population. That doesn’t mean the data we collect from interviews doesn’t have value, it just has different uses.
There are two broad types of samples, with several different techniques clustered below those. Probability sampling is associated with surveys, and non-probability sampling is often used when conducting interviews. We’ll first describe probability samples, before discussing the non-probability options.
The type of sampling you’ll use will be based on the type of research you’re intending to do. There’s no sample that’s right or wrong, they can just be more or less appropriate for the question you’re trying to answer. And if you use a less appropriate sampling strategy, the answer you get through your research is less likely to be accurate.
7.1 Types of Probability Samples
So we just hinted at the idea that depending on the sample you use, you can generalize the data you collect from the sample to the population. That will depend though on whether your sample represents the population. To ensure that your sample is representative of the population, you will want to use a probability sample. A representative sample refers to whether the characteristics (race, age, income, education, etc) of the sample are the same as the population. Probability sampling is a sampling technique in which every individual in the population has an equal chance of being selected as a subject for the research.
There are several different types of probability samples you can use, depending on the resources you have available.
Let’s start with a simple random sample . In order to use a simple random sample all you have to do is take everyone in your population, throw them in a hat (not literally, you can just throw their names in a hat), and choose the number of names you want to use for your sample. By drawing blindly, you can eliminate human bias in constructing the sample and your sample should represent the population from which it is being taken.
However, a simple random sample isn’t quite that easy to build. The biggest issue is that you have to know who everyone is in order to randomly select them. What that requires is a sampling frame , a list of all residents in the population. But we don’t always have that. There is no list of residents of New York City (or any other city). Organizations that do have such a list wont just give it away. Try to ask your university for a list and contact information of everyone at your school so you can do a survey? They wont give it to you, for privacy reasons. It’s actually harder to think of popultions you could easily develop a sample frame for than those you can’t. If you can get or build a sampling frame, the work of a simple random sample is fairly simple, but that’s the biggest challenge.
Most of the time a true sampling frame is impossible to acquire, so researcher have to settle for something approximating a complete list. Earlier generations of researchers could use the random dial method to contact a random sample of Americans, because every household had a single phone. To use it you just pick up the phone and dial random numbers. Assuming the numbers are actually random, anyone might be called. That method actually worked somewhat well, until people stopped having home phone numbers and eventually stopped answering the phone. It’s a fun mental exercise to think about how you would go about creating a sampling frame for different groups though; think through where you would look to find a list of everyone in these groups:
Plumbers Recent first-time fathers Members of gyms
The best way to get an actual sampling frame is likely to purchase one from a private company that buys data on people from all the different websites we use.
Let’s say you do have a sampling frame though. For instance, you might be hired to do a survey of members of the Republican Party in the state of Utah to understand their political priorities this year, and the organization could give you a list of their members because they’ve hired you to do the reserach. One method of constructing a simple random sample would be to assign each name on the list a number, and then produce a list of random numbers. Once you’ve matched the random numbers to the list, you’ve got your sample. See the example using the list of 20 names below

and the list of 5 random numbers.

Systematic sampling is similar to simple random sampling in that it begins with a list of the population, but instead of choosing random numbers one would select every kth name on the list. What the heck is a kth? K just refers to how far apart the names are on the list you’re selecting. So if you want to sample one-tenth of the population, you’d select every tenth name. In order to know the k for your study you need to know your sample size (say 1000) and the size of the population (75000). You can divide the size of the population by the sample (75000/1000), which will produce your k (750). As long as the list does not contain any hidden order, this sampling method is as good as the random sampling method, but its only advantage over the random sampling technique is simplicity. If we used the same list as above and wanted to survey 1/5th of the population, we’d include 4 of the names on the list. It’s important with systematic samples to randomize the starting point in the list, otherwise people with A names will be oversampled. If we started with the 3rd name, we’d select Annabelle Frye, Cristobal Padilla, Jennie Vang, and Virginia Guzman, as shown below. So in order to use a systematic sample, we need three things, the population size (denoted as N ), the sample size we want ( n ) and k , which we calculate by dividing the population by the sample).
N= 20 (Population Size) n= 4 (Sample Size) k= 5 {20/4 (kth element) selection interval}

We can also use a stratified sample , but that requires knowing more about the population than just their names. A stratified sample divides the study population into relevant subgroups, and then draws a sample from each subgroup. Stratified sampling can be used if you’re very concerned about ensuring balance in the sample or there may be a problem of underrepresentation among certain groups when responses are received. Not everyone in your sample is equally likely to answer a survey. Say for instance we’re trying to predict who will win an election in a county with three cities. In city A there are 1 million college students, in city B there are 2 million families, and in City C there are 3 million retirees. You know that retirees are more likely than busy college students or parents to respond to a poll. So you break the sample into three parts, ensuring that you get 100 responses from City A, 200 from City B, and 300 from City C, so the three cities would match the population. A stratified sample provides the researcher control over the subgroups that are included in the sample, whereas simple random sampling does not guarantee that any one type of person will be included in the final sample. A disadvantage is that it is more complex to organize and analyze the results compared to simple random sampling.
Cluster sampling is an approach that begins by sampling groups (or clusters) of population elements and then selects elements from within those groups. A researcher would use cluster sampling if getting access to elements in an entrie population is too challenging. For instance, a study on students in schools would probably benefit from randomly selecting from all students at the 36 elementary schools in a fictional city. But getting contact information for all students would be very difficult. So the researcher might work with principals at several schools and survey those students. The researcher would need to ensure that the students surveyed at the schools are similar to students throughout the entire city, and greater access and participation within each cluster may make that possible.
The image below shows how this can work, although the example is oversimplified. Say we have 12 students that are in 6 classrooms. The school is in total 1/4th green (3/12), 1/4th yellow (3/12), and half blue (6/12). By selecting the right clusters from within the school our sample can be representative of the entire school, assuming these colors are the only significant difference between the students. In the real world, you’d want to match the clusters and population based on race, gender, age, income, etc. And I should point out that this is an overly simplified example. What if 5/12s of the school was yellow and 1/12th was green, how would I get the right proportions? I couldn’t, but you’d do the best you could. You still wouldn’t want 4 yellows in the sample, you’d just try to approximiate the population characteristics as best you can.

7.2 Actually Doing a Survey
All of that probably sounds pretty complicated. Identifying your population shouldn’t be too difficult, but how would you ever get a sampling frame? And then actually identifying who to include… It’s probably a bit overwhelming and makes doing a good survey sound impossible.
Researchers using surveys aren’t superhuman though. Often times, they use a little help. Because surveys are really valuable, and because researchers rely on them pretty often, there has been substantial growth in companies that can help to get one’s survey to its intended audience.
One popular resource is Amazon’s Mechanical Turk (more commonly known as MTurk). MTurk is at its most basic a website where workers look for jobs (called hits) to be listed by employers, and choose whether to do the task or not for a set reward. MTurk has grown over the last decade to be a common source of survey participants in the social sciences, in part because hiring workers costs very little (you can get some surveys completed for penny’s). That means you can get your survey completed with a small grant ($1-2k at the low end) and get the data back in a few hours. Really, it’s a quick and easy way to run a survey.
However, the workers aren’t perfectly representative of the average American. For instance, researchers have found that MTurk respondents are younger, better educated, and earn less than the average American.
One way to get around that issue, which can be used with MTurk or any survey, is to weight the responses. Because with MTurk you’ll get fewer responses from older, less educated, and richer Americans, those responses you do give you want to count for more to make your sample more representative of the population. Oversimplified example incoming!
Imagine you’re setting up a pizza party for your class. There are 9 people in your class, 4 men and 5 women. You only got 4 responses from the men, and 3 from the women. All 4 men wanted peperoni pizza, while the 3 women want a combination. Pepperoni wins right, 4 to 3? Not if you assume that the people that didn’t respond are the same as the ones that did. If you weight the responses to match the population (the full class of 9), a combination pizza is the winner.

Because you know the population of women is 5, you can weight the 3 responses from women by 5/3 = 1.6667. If we weight (or multiply) each vote we did receive from a woman by 1.6667, each vote for a combination now equals 1.6667, meaning that the 3 votes for combination total 5. Because we received a vote from every man in the class, we just weight their votes by 1. The big assumption we have to make is that the people we didn’t hear from (the 2 women that didn’t vote) are similar to the ones we did hear from. And if we don’t get any responses from a group we don’t have anything to infer their preferences or views from.
Let’s go through a slightly more complex example, still just considering one quality about people in the class. Let’s say your class actually has 100 students, but you only received votes from 50. And, what type of pizza people voted for is mixed, but men still prefer peperoni overall, and women still prefer combination. The class is 60% female and 40% male.
We received 21 votes from women out of the 60, so we can weight their responses by 60/21 to represent the population. We got 29 votes out of the 40 for men, so their responses can be weighted by 40/29. See the math below.

53.8 votes for combination? That might seem a little odd, but weighting isn’t a perfect science. We can’t identify what a non-respondent would have said exactly, all we can do is use the responses of other similar people to make a good guess. That issue often comes up in polling, where pollsters have to guess who is going to vote in a given election in order to project who will win. And we can weight on any characteristic of a person we think will be important, alone or in combination. Modern polls weight on age, gender, voting habits, education, and more to make the results as generalizable as possible.
There’s an appendix later in this book where I walk through the actual steps of creating weights for a sample in R, if anyone actually does a survey. I intended this section to show that doing a good survey might be simpler than it seemed, but now it might sound even more difficult. A good lesson to take though is that there’s always another door to go through, another hurdle to improve your methods. Being good at research just means being constantly prepared to be given a new challenge, and being able to find another solution.
7.3 Non-Probability Sampling
Qualitative researchers’ main objective is to gain an in-depth understanding on the subject matter they are studying, rather than attempting to generalize results to the population. As such, non-probability sampling is more common because of the researchers desire to gain information not from random elements of the population, but rather from specific individuals.
Random selection is not used in nonprobability sampling. Instead, the personal judgment of the researcher determines who will be included in the sample. Typically, researchers may base their selection on availability, quotas, or other criteria. However, not all members of the population are given an equal chance to be included in the sample. This nonrandom approach results in not knowing whether the sample represents the entire population. Consequently, researchers are not able to make valid generalizations about the population.
As with probability sampling, there are several types of non-probability samples. Convenience sampling , also known as accidental or opportunity sampling, is a process of choosing a sample that is easily accessible and readily available to the researcher. Researchers tend to collect samples from convenient locations such as their place of employment, a location, school, or other close affiliation. Although this technique allows for quick and easy access to available participants, a large part of the population is excluded from the sample.
For example, researchers (particularly in psychology) often rely on research subjects that are at their universities. That is highly convenient, students are cheap to hire and readily available on campuses. However, it means the results of the study may have limited ability to predict motivations or behaviors of people that aren’t included in the sample, i.e., people outside the age of 18-22 that are going to college.
If I ask you to get find out whether people approve of the mayor or not, and tell you I want 500 people’s opinions, should you go stand in front of the local grocery store? That would be convinient, and the people coming will be random, right? Not really. If you stand outside a rural Piggly Wiggly or an urban Whole Foods, do you think you’ll see the same people? Probably not, people’s chracteristics make the more or less likely to be in those locations. This technique runs the high risk of over- or under-representation, biased results, as well as an inability to make generalizations about the larger population. As the name implies though, it is convenient.
Purposive sampling , also known as judgmental or selective sampling, refers to a method in which the researcher decides who will be selected for the sample based on who or what is relevant to the study’s purpose. The researcher must first identify a specific characteristic of the population that can best help answer the research question. Then, they can deliberately select a sample that meets that particular criterion. Typically, the sample is small with very specific experiences and perspectives. For instance, if I wanted to understand the experiences of prominent foreign-born politicians in the United States, I would purposefully build a sample of… prominent foreign-born politicians in the United States. That would exclude anyone that was born in the United States or and that wasn’t a politician, and I’d have to define what I meant by prominent. Purposive sampling is susceptible to errors in judgment by the researcher and selection bias due to a lack of random sampling, but when attempting to research small communities it can be effective.
When dealing with small and difficult to reach communities researchers sometimes use snowball samples , also known as chain referral sampling. Snowball sampling is a process in which the researcher selects an initial participant for the sample, then asks that participant to recruit or refer additional participants who have similar traits as them. The cycle continues until the needed sample size is obtained.
This technique is used when the study calls for participants who are hard to find because of a unique or rare quality or when a participant does not want to be found because they are part of a stigmatized group or behavior. Examples may include people with rare diseases, sex workers, or a child sex offenders. It would be impossible to find an accurate list of sex workers anywhere, and surveying the general population about whether that is their job will produce false responses as people will be unwilling to identify themselves. As such, a common method is to gain the trust of one individual within the community, who can then introduce you to others. It is important that the researcher builds rapport and gains trust so that participants can be comfortable contributing to the study, but that must also be balanced by mainting objectivity in the research.
Snowball sampling is a useful method for locating hard to reach populations but cannot guarantee a representative sample because each contact will be based upon your last. For instance, let’s say you’re studying illegal fight clubs in your state. Some fight clubs allow weapons in the fights, while others completely ban them; those two types of clubs never interreact because of their disagreement about whether weapons should be allowed, and there’s no overlap between them (no members in both type of club). If your initial contact is with a club that uses weapons, all of your subsequent contacts will be within that community and so you’ll never understand the differences. If you didn’t know there were two types of clubs when you started, you’ll never even know you’re only researching half of the community. As such, snowball sampling can be a necessary technique when there are no other options, but it does have limitations.
Quota Sampling is a process in which the researcher must first divide a population into mutually exclusive subgroups, similar to stratified sampling. Depending on what is relevant to the study, subgroups can be based on a known characteristic such as age, race, gender, etc. Secondly, the researcher must select a sample from each subgroup to fit their predefined quotas. Quota sampling is used for the same reason as stratified sampling, to ensure that your sample has representation of certain groups. For instance, let’s say that you’re studying sexual harassment in the workplace, and men are much more willing to discuss their experiences than women. You might choose to decide that half of your final sample will be women, and stop requesting interviews with men once you fill your quota. The core difference is that while stratified sampling chooses randomly from within the different groups, quota sampling does not. A quota sample can either be proportional or non-proportional . Proportional quota sampling refers to ensuring that the quotas in the sample match the population (if 35% of the company is female, 35% of the sample should be female). Non-proportional sampling allows you to select your own quota sizes. If you think the experiences of females with sexual harassment are more important to your research, you can include whatever percentage of females you desire.
7.4 Dangers in sampling
Now that we’ve described all the different ways that one could create a sample, we can talk more about the pitfalls of sampling. Ensuring a quality sample means asking yourself some basic questions:
- Who is in the sample?
- How were they sampled?
- Why were they sampled?
A meal is often only as good as the ingredients you use, and your data will only be as good as the sample. If you collect data from the wrong people, you’ll get the wrong answer. You’ll still get an answer, it’ll just be inaccurate. And I want to reemphasize here wrong people just refers to inappropriate for your study. If I want to study bullying in middle schools, but I only talk to people that live in a retirement home, how accurate or relevant will the information I gather be? Sure, they might have grandchildren in middle school, and they may remember their experiences. But wouldn’t my information be more relevant if I talked to students in middle school, or perhaps a mix of teachers, parents, and students? I’ll get an answer from retirees, but it wont be the one I need. The sample has to be appropriate to the research question.
Is a bigger sample always better? Not necessarily. A larger sample can be useful, but a more representative one of the population is better. That was made painfully clear when the magazine Literary Digest ran a poll to predict who would win the 1936 presidential election between Alf Landon and incumbent Franklin Roosevelt. Literary Digest had run the poll since 1916, and had been correct in predicting the outcome every time. It was the largest poll ever, and they received responses for 2.27 million people. They essentially received responses from 1 percent of the American population, while many modern polls use only 1000 responses for a much more populous country. What did they predict? They showed that Alf Landon would be the overwhelming winner, yet when the election was held Roosevelt won every state except Maine and Vermont. It was one of the most decisive victories in Presidential history.
So what went wrong for the Literary Digest? Their poll was large (gigantic!), but it wasn’t representative of likely voters. They polled their own readership, which tended to be more educated and wealthy on average, along with people on a list of those with registered automobiles and telephone users (both of which tended to be owned by the wealthy at that time). Thus, the poll largely ignored the majority of Americans, who ended up voting for Roosevelt. The Literary Digest poll is famous for being wrong, but led to significant improvements in the science of polling to avoid similar mistakes in the future. Researchers have learned a lot in the century since that mistake, even if polling and surveys still aren’t (and can’t be) perfect.
What kind of sampling strategy did Literary Digest use? Convenience, they relied on lists they had available, rather than try to ensure every American was included on their list. A representative poll of 2 million people will give you more accurate results than a representative poll of 2 thousand, but I’ll take the smaller more representative poll than a larger one that uses convenience sampling any day.
7.5 Summary
Picking the right type of sample is critical to getting an accurate answer to your reserach question. There are a lot of differnet options in how you can select the people to participate in your research, but typically only one that is both correct and possible depending on the research you’re doing. In the next chapter we’ll talk about a few other methods for conducting reseach, some that don’t include any sampling by you.
An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .
- Advanced Search
- Journal List
- An Bras Dermatol
- v.91(3); May-Jun 2016
Sampling: how to select participants in my research study? *
Jeovany martínez-mesa.
1 Faculdade Meridional (IMED) - Passo Fundo (RS), Brazil.
David Alejandro González-Chica
2 University of Adelaide - Adelaide, Australia.
Rodrigo Pereira Duquia
3 Universidade Federal de Ciências da Saúde de Porto Alegre (UFCSPA) - Porto Alegre (RS), Brazil.

Renan Rangel Bonamigo
João luiz bastos.
4 Universidade Federal de Santa Catarina (UFSC) - Florianópolis (RS), Brazil.
In this paper, the basic elements related to the selection of participants for a health research are discussed. Sample representativeness, sample frame, types of sampling, as well as the impact that non-respondents may have on results of a study are described. The whole discussion is supported by practical examples to facilitate the reader's understanding.
To introduce readers to issues related to sampling.
INTRODUCTION
The essential topics related to the selection of participants for a health research are: 1) whether to work with samples or include the whole reference population in the study (census); 2) the sample basis; 3) the sampling process and 4) the potential effects nonrespondents might have on study results. We will refer to each of these aspects with theoretical and practical examples for better understanding in the sections that follow.
TO SAMPLE OR NOT TO SAMPLE
In a previous paper, we discussed the necessary parameters on which to estimate the sample size. 1 We define sample as a finite part or subset of participants drawn from the target population. In turn, the target population corresponds to the entire set of subjects whose characteristics are of interest to the research team. Based on results obtained from a sample, researchers may draw their conclusions about the target population with a certain level of confidence, following a process called statistical inference. When the sample contains fewer individuals than the minimum necessary, but the representativeness is preserved, statistical inference may be compromised in terms of precision (prevalence studies) and/or statistical power to detect the associations of interest. 1 On the other hand, samples without representativeness may not be a reliable source to draw conclusions about the reference population (i.e., statistical inference is not deemed possible), even if the sample size reaches the required number of participants. Lack of representativeness can occur as a result of flawed selection procedures (sampling bias) or when the probability of refusal/non-participation in the study is related to the object of research (nonresponse bias). 1 , 2
Although most studies are performed using samples, whether or not they represent any target population, census-based estimates should be preferred whenever possible. 3 , 4 For instance, if all cases of melanoma are available on a national or regional database, and information on the potential risk factors are also available, it would be preferable to conduct a census instead of investigating a sample.
However, there are several theoretical and practical reasons that prevent us from carrying out census-based surveys, including:
- Ethical issues: it is unethical to include a greater number of individuals than that effectively required;
- Budgetary limitations: the high costs of a census survey often limits its use as a strategy to select participants for a study;
- Logistics: censuses often impose great challenges in terms of required staff, equipment, etc. to conduct the study;
- Time restrictions: the amount of time needed to plan and conduct a census-based survey may be excessive; and,
- Unknown target population size: if the study objective is to investigate the presence of premalignant skin lesions in illicit drugs users, lack of information on all existing users makes it impossible to conduct a census-based study.
All these reasons explain why samples are more frequently used. However, researchers must be aware that sample results can be affected by the random error (or sampling error). 3 To exemplify this concept, we will consider a research study aiming to estimate the prevalence of premalignant skin lesions (outcome) among individuals >18 years residing in a specific city (target population). The city has a total population of 4,000 adults, but the investigator decided to collect data on a representative sample of 400 participants, detecting an 8% prevalence of premalignant skin lesions. A week later, the researcher selects another sample of 400 participants from the same target population to confirm the results, but this time observes a 12% prevalence of premalignant skin lesions. Based on these findings, is it possible to assume that the prevalence of lesions increased from the first to the second week? The answer is probably not. Each time we select a new sample, it is very likely to obtain a different result. These fluctuations are attributed to the "random error." They occur because individuals composing different samples are not the same, even though they were selected from the same target population. Therefore, the parameters of interest may vary randomly from one sample to another. Despite this fluctuation, if it were possible to obtain 100 different samples of the same population, approximately 95 of them would provide prevalence estimates very close to the real estimate in the target population - the value that we would observe if we investigated all the 4,000 adults residing in the city. Thus, during the sample size estimation the investigator must specify in advance the highest or maximum acceptable random error value in the study. Most population-based studies use a random error ranging from 2 to 5 percentage points. Nevertheless, the researcher should be aware that the smaller the random error considered in the study, the larger the required sample size. 1
SAMPLE FRAME
The sample frame is the group of individuals that can be selected from the target population given the sampling process used in the study. For example, to identify cases of cutaneous melanoma the researcher may consider to utilize as sample frame the national cancer registry system or the anatomopathological records of skin biopsies. Given that the sample may represent only a portion of the target population, the researcher needs to examine carefully whether the selected sample frame fits the study objectives or hypotheses, and especially if there are strategies to overcome the sample frame limitations (see Chart 1 for examples and possible limitations).
Examples of sample frames and potential limitations as regards representativeness
| Sample frames | Limitations |
|---|---|
| Population census | • If the census was not conducted in recent years, areas with high migration might be outdated |
| • Homeless or itinerant people cannot be represented | |
| Hospital or Health Services records | • Usually include only data of affected people (this is a limitation, depending on the study objectives) |
| • Depending on the service, data may be incomplete and/or outdated | |
| • If the lists are from public units, results may differ from those who seek private services | |
| School lists | • School lists are currently available only in the public sector |
| • Children/ teenagers not attending school will not be represented | |
| • Lists are quickly outdated | |
| • There will be problems in areas with high percentage of school absenteeism | |
| List of phone numbers | • Several population groups are not represented: individuals with no phone line at home (low-income families, young people who use only cell phones), those who spend less time at home, etc. |
| Mailing lists | • Individuals with multiple email addresses, which increase the chance of selection compared to individuals with only one address |
| • Individuals without an email address may be different from those who have it, according to age, education, etc. | |
Sampling can be defined as the process through which individuals or sampling units are selected from the sample frame. The sampling strategy needs to be specified in advance, given that the sampling method may affect the sample size estimation. 1 , 5 Without a rigorous sampling plan the estimates derived from the study may be biased (selection bias). 3
TYPES OF SAMPLING
In figure 1 , we depict a summary of the main sampling types. There are two major sampling types: probabilistic and nonprobabilistic.

Sampling types used in scientific studies
NONPROBABILISTIC SAMPLING
In the context of nonprobabilistic sampling, the likelihood of selecting some individuals from the target population is null. This type of sampling does not render a representative sample; therefore, the observed results are usually not generalizable to the target population. Still, unrepresentative samples may be useful for some specific research objectives, and may help answer particular research questions, as well as contribute to the generation of new hypotheses. 4 The different types of nonprobabilistic sampling are detailed below.
Convenience sampling : the participants are consecutively selected in order of apperance according to their convenient accessibility (also known as consecutive sampling). The sampling process comes to an end when the total amount of participants (sample saturation) and/or the time limit (time saturation) are reached. Randomized clinical trials are usually based on convenience sampling. After sampling, participants are usually randomly allocated to the intervention or control group (randomization). 3 Although randomization is a probabilistic process to obtain two comparable groups (treatment and control), the samples used in these studies are generally not representative of the target population.
Purposive sampling: this is used when a diverse sample is necessary or the opinion of experts in a particular field is the topic of interest. This technique was used in the study by Roubille et al, in which recommendations for the treatment of comorbidities in patients with rheumatoid arthritis, psoriasis, and psoriatic arthritis were made based on the opinion of a group of experts. 6
Quota sampling: according to this sampling technique, the population is first classified by characteristics such as gender, age, etc. Subsequently, sampling units are selected to complete each quota. For example, in the study by Larkin et al., the combination of vemurafenib and cobimetinib versus placebo was tested in patients with locally-advanced melanoma, stage IIIC or IV, with BRAF mutation. 7 The study recruited 495 patients from 135 health centers located in several countries. In this type of study, each center has a "quota" of patients.
"Snowball" sampling : in this case, the researcher selects an initial group of individuals. Then, these participants indicate other potential members with similar characteristics to take part in the study. This is frequently used in studies investigating special populations, for example, those including illicit drugs users, as was the case of the study by Gonçalves et al, which assessed 27 users of cocaine and crack in combination with marijuana. 8
PROBABILISTIC SAMPLING
In the context of probabilistic sampling, all units of the target population have a nonzero probability to take part in the study. If all participants are equally likely to be selected in the study, equiprobabilistic sampling is being used, and the odds of being selected by the research team may be expressed by the formula: P=1/N, where P equals the probability of taking part in the study and N corresponds to the size of the target population. The main types of probabilistic sampling are described below.
Simple random sampling: in this case, we have a full list of sample units or participants (sample basis), and we randomly select individuals using a table of random numbers. An example is the study by Pimenta et al, in which the authors obtained a listing from the Health Department of all elderly enrolled in the Family Health Strategy and, by simple random sampling, selected a sample of 449 participants. 9
Systematic random sampling: in this case, participants are selected from fixed intervals previously defined from a ranked list of participants. For example, in the study of Kelbore et al, children who were assisted at the Pediatric Dermatology Service were selected to evaluate factors associated with atopic dermatitis, selecting always the second child by consulting order. 10
Stratified sampling: in this type of sampling, the target population is first divided into separate strata. Then, samples are selected within each stratum, either through simple or systematic sampling. The total number of individuals to be selected in each stratum can be fixed or proportional to the size of each stratum. Each individual may be equally likely to be selected to participate in the study. However, the fixed method usually involves the use of sampling weights in the statistical analysis (inverse of the probability of selection or 1/P). An example is the study conducted in South Australia to investigate factors associated with vitamin D deficiency in preschool children. Using the national census as the sample frame, households were randomly selected in each stratum and all children in the age group of interest identified in the selected houses were investigated. 11
Cluster sampling: in this type of probabilistic sampling, groups such as health facilities, schools, etc., are sampled. In the above-mentioned study, the selection of households is an example of cluster sampling. 11
Complex or multi-stage sampling: This probabilistic sampling method combines different strategies in the selection of the sample units. An example is the study of Duquia et al. to assess the prevalence and factors associated with the use of sunscreen in adults. The sampling process included two stages. 12 Using the 2000 Brazilian demographic census as sampling frame, all 404 census tracts from Pelotas (Southern Brazil) were listed in ascending order of family income. A sample of 120 tracts were systematically selected (first sampling stage units). In the second stage, 12 households in each of these census tract (second sampling stage units) were systematically drawn. All adult residents in these households were included in the study (third sampling stage units). All these stages have to be considered in the statistical analysis to provide correct estimates.
NONRESPONDENTS
Frequently, sample sizes are increased by 10% to compensate for potential nonresponses (refusals/losses). 1 Let us imagine that in a study to assess the prevalence of premalignant skin lesions there is a higher percentage of nonrespondents among men (10%) than among women (1%). If the highest percentage of nonresponse occurs because these men are not at home during the scheduled visits, and these participants are more likely to be exposed to the sun, the number of skin lesions will be underestimated. For this reason, it is strongly recommended to collect and describe some basic characteristics of nonrespondents (sex, age, etc.) so they can be compared to the respondents to evaluate whether the results may have been affected by this systematic error.
Often, in study protocols, refusal to participate or sign the informed consent is considered an "exclusion criteria". However, this is not correct, as these individuals are eligible for the study and need to be reported as "nonrespondents".
SAMPLING METHOD ACCORDING TO THE TYPE OF STUDY
In general, clinical trials aim to obtain a homogeneous sample which is not necessarily representative of any target population. Clinical trials often recruit those participants who are most likely to benefit from the intervention. 3 Thus, the more strict criteria for inclusion and exclusion of subjects in clinical trials often make it difficult to locate participants: after verification of the eligibility criteria, just one out of ten possible candidates will enter the study. Therefore, clinical trials usually show limitations to generalize the results to the entire population of patients with the disease, but only to those with similar characteristics to the sample included in the study. These peculiarities in clinical trials justify the necessity of conducting a multicenter and/or global studiesto accelerate the recruitment rate and to reach, in a shorter time, the number of patients required for the study. 13
In turn, in observational studies to build a solid sampling plan is important because of the great heterogeneity usually observed in the target population. Therefore, this heterogeneity has to be also reflected in the sample. A cross-sectional population-based study aiming to assess disease estimates or identify risk factors often uses complex probabilistic sampling, because the sample representativeness is crucial. However, in a case-control study, we face the challenge of selecting two different samples for the same study. One sample is formed by the cases, which are identified based on the diagnosis of the disease of interest. The other consists of controls, which need to be representative of the population that originated the cases. Improper selection of control individuals may introduce selection bias in the results. Thus, the concern with representativeness in this type of study is established based on the relationship between cases and controls (comparability).
In cohort studies, individuals are recruited based on the exposure (exposed and unexposed subjects), and they are followed over time to evaluate the occurrence of the outcome of interest. At baseline, the sample can be selected from a representative sample (population-based cohort studies) or a non-representative sample. However, in the successive follow-ups of the cohort member, study participants must be a representative sample of those included in the baseline. 14 , 15 In this type of study, losses over time may cause follow-up bias.
Researchers need to decide during the planning stage of the study if they will work with the entire target population or a sample. Working with a sample involves different steps, including sample size estimation, identification of the sample frame, and selection of the sampling method to be adopted.
Financial Support: None.
* Study performed at Faculdade Meridional - Escola de Medicina (IMED) - Passo Fundo (RS), Brazil.
- How it works

Population vs Sample – Definitions, Types & Examples
Published by Alvin Nicolas at September 20th, 2021 , Revised On July 19, 2023
Wondering who wins in the Population vs. Sample battle? Don’t know which one to choose for your survey?
If you are hunting similar questions, congratulations, you have come to the right place.
The Sample and Population sections tend to be a stumbling block for most students, if not all. And if you are one of those people, now is the perfect time to seize an opportunity. This guide contains all the information in the world to sweep through the methodology section of your dissertation proficiently.
Sounds interesting? Let’s get started then!
What is Population in Research?
Population in the research market comprises all the members of a defined group that you generalize to find the results of your study. This means the exact population will always depend on the scope of your respected study. Population in research is not limited to assessing humans; it can be any data parameter, including events, objects, histories, and more possessing a common trait. The measurable quality of the population is called a parameter .
For instance…
If you are to evaluate findings for Health Concerns of Women , you might have to consider all the women in the world that are dead, alive, and will live in the future.
|
|
Types of Population
Though there are different types and sub-categories of population, below are the four most common yet important ones to consider.
Countable Population
As the term itself explains, this type of population is one that can be numbered and calculated. It is also known as finite population . An example of a finite or countable population would be all the students in a college or potential buyers of a brand. A countable population in statistical analysis is thought to be of more benefit than other types.
Uncountable Population
The uncountable population, primarily known as an infinite population, is where the counting units are beyond one’s consideration and capabilities. For instance, the number of rice grains in the field. Or the total number of protons and electrons on a blank page. The fact that this type of population cannot be calculated often leaves room for error and uncertainty.
Hypothetical Population
This is the population whose unit is not available in a tangible form. Although the population in research analysis includes all sets of possible observations, events, and objects, there still are situations that can only be hypothetical. The perfect example to explain this would be the population of the world. You can give an estimated and hypothetical value gathered by different governments, but can you count all humans existing on the planet? Certainly, no! Another example would be the outcome of rolling dice.
Existent Population
The existent population is the opposite of a hypothetical population, i.e., everything is countable in a concrete form. All the notebooks and pens of students of a particular class could be an example of an existent population.
Is all clear?
Let us move on to the next important term of this guide.
What is Sample in Research?
In quantitative research methodology , the sample is a set of collected data from a defined procedure. It is basically a much smaller part of the whole, i.e., population. The sample depicts all the members of the population that are under observation when conducting research surveys . It can be further assessed to find out about the behavior of the entire population data. The measurable quality of the sample is called a statistic .
Say you send a research questionnaire to all the 200 contacts on your phone, and 42 of them end up filling up the forms. Your sample here is the 42 contacts that participated in the study. The rest of the people who did not participate but were sent invitations become part of your sampling frame . The sampling frame is the group of people who could possibly be in your research or can be a good fit, which here are the 158 people on your phone.
Can you think of more examples?
Before we start with the sampling types, here are a few other terminologies related to sampling for a better understanding.
Sample Size : the total number of people selected for the survey/study
Sample Technique : The technique you use in order to get your desired sample size.
Pro Tip: Use a sample for your research when you have a larger population, and you want to generalize your findings for the entire population from this sample.
What data collection best suits your research?
- Find out by hiring an expert from ResearchProspect today!
- Despite how challenging the subject may be, we are here to help you.
Types of Sampling Methods
There are two major types of sampling; Probability Sampling and Non-probability Sampling.
Probability Sampling
In this type of sampling, the researcher tends to set a selection of a few criteria and selects members of a population randomly. This means all the members have an equal chance to be a part of the study.
For example, you are to examine a bag containing rice or some other food item. Now any small portion or part you take for observation will be a true representative of the whole food bag.
It is further divided into the following five types:
- Simple Random Sampling
In this type of probability sampling, the members of the study are chosen by chance or randomly. Wondering if this affects the overall quality of your research? Well, it does not. The fact that every member has an equal chance of being selected, this random selection will do just as fine and speak well for the whole group. The only thing you need to make sure of is that the population is homogenous , like the bag of rice.
- Systematic Sampling
In systematic sampling, the researcher will select a member after a fixed interval of time. The member selected for the study after this fixed interval is known as the Kth element.
For example, if the researcher decides to select a member occurring after every 30 members, the Kth element here would be the 30th element.
- Stratified Random Sampling
If you know the meaning of strata, you might have guessed by now what stratified random sampling is. So, in this type of sampling, the population is first divided into sub-categories. There is no hard and fast rule for it; it is all done randomly.
So, when do we need this kind of sampling?
Stratified random sampling is adopted when the population is not homogenous. It is first divided into groups and categories based on similarities, and later members from each group are randomly selected. The idea is to address the problem of less homogeneity of the population to get a truly representative sample.
- Cluster Sampling
This is where researchers divide the population into clusters that tend to represent the whole population. They are usually divided based on demographic parameters , such as location, age, and sex. It can be a little difficult than the ones earlier mentioned, but cluster sampling is one of the most effective ways to derive interface from the feedback.
For example, suppose the United States government wishes to evaluate the number of people taking the first dose of the COVID-19 vaccine. In that case, they can divide it into groups based on various country estates. Not only will the results be accurate using this sampling method, but it will also be easier for future diagnoses.
- Multi-stage Sampling
Multi-stage sampling is similar to cluster sampling, but let’s say, a complex form of it. In this type of cluster sampling, all the clusters are further divided into sub-clusters. It involves multiple stages, thus the name. Initially, the naturally occurring categories in a population are chosen as clusters, then each cluster is categorized into smaller clusters, and lastly, members are selected from each smaller cluster.
How many stages are enough?
Well, that depends on the nature of your study/research. For some, two to three would be more than enough, while others can take up to 10 rounds or more.
Non-Probability Sampling
Non-probability sampling is the other sampling type where you cannot calculate the probability or chances of any members selected for research. In other words, it is everything the probability sampling is NOT. We just figured out that probability sampling includes selection by chance; this one depends on the subjective judgment of the researcher.
For example, one member might have a 20 percent chance of getting selected in non-probability sampling, while another could have a 60 percent chance.
Get statistical analysis help at an affordable price
- An expert statistician will complete your work
- Rigorous quality checks
- Confidentiality and reliability
- Any statistical software of your choice
- Free Plagiarism Report

Which type of sampling do you think is better?
The debate on this might prevail forever because there is no correct answer for this. Both have their advantages and disadvantages. While non-probability sampling cannot be reliable, it does save your time and costs. Similarly, if probability sampling yields accurate results, it also is not easy to use and sometimes impossible to be conducted, especially when you have a small population at hand.
Types of Non-Probability Sampling
The Four types of non-probability sampling are:
|
| |||
|---|---|---|---|
- Convenience Sampling
Convenience sampling relies on the ease of access to specific subjects such as students in the college café or pedestrians on the road. If the researcher can conveniently get the sample for their study, it will fall under this type of sampling. This type of sampling is usually effective when researchers lack time, resources, and money. They have almost zero authority to choose the sample elements and are purely done on immediacy. You send your questionnaire to random contacts on your phone would be convenience sampling as you did not walk extra miles to get the job done.
- Purposive Sampling
Purposive sampling is also known as judgmental sampling because researchers here would effectively consider the study’s purpose and some understanding of what to expect from the target audience. In other words, the target audience is defined here. For instance, if a study is conducted exclusively for Coronavirus patients, all others not affected by the virus will automatically be rejected or excluded from the study.
- Quota Sampling
For quota sampling, you need to have a pre-set standard of sample selection. What happens in quota sampling is that the sample is formed on the basis of specific attributes so that the qualities of this sample can be found in the total population. Slightly complex but worth the hassle.
- Snowball Sampling
Lastly, this type of non-probability sampling is applied when the subjects are rare and difficult to get. For example, if you are to trace and research drug dealers, it would be almost impossible to get them interviewed for the study. This is where snowball sampling comes into play. Similarly, writing a paper on the mental health of rape victims would also be a hard row to hoe. In such a situation, you will only tract a few sources/members and base the rest of your research on it.
To put it briefly, your sample is the group of people participating in the study, while the population is the total number of people to whom the results will apply. As an analogy, if the sample is the garden in your house, the population will be the forests out there.
Now that you have all the details on these two, can you spot three differences between population and sample ?
Well, we are sure you can give more than just three.
Here are a few differences in case you need a quick revision.
Differences between Population and Sample
| Sample | Population |
|---|---|
| Part of a larger group/population | The whole group |
| Characteristics are known as statistics | Characteristics are called parameters |
| The statistics are predicted/known | Parameters are unknown/unpredictable |
| Has a margin of error | True representation of opinion |
| Example: Top 10 students of the class | Example: All the students of the class |
This brings us to the end of this guide. We hope you are now clear on these topics and have made up your mind to use a sample for your research or population. The final choice is yours; however, make sure to keep all the above-mentioned facts and particulars in mind and see what works best for you.
Meanwhile, if you have questions and queries or wish to add to this guide, please drop a comment in the comments section below.
FAQs About Population vs. Sample
How can you identify a sample and population.
Sample is the specific group you collect data from, and the population is the entire group you deduce conclusions about. The population is the bigger sample size.
What is a population parameter?
Parameter is some characteristic of the population that cannot be studied directly. It is usually estimated by numbers and figures calculated from the sample data.
Is it better to use a sample instead of a population?
Yes, if you looking for a cost-effective and easier way, a sample is the better option.
What is an example of statistics?
If one office is the sample of the population of all offices in a building, then the average of salaries earned by all employees in the sample office annually would be an example of a statistic .
Does a sample represent the entire population?
Not always. Only a representative sample reflects the entire population of your study. It is an unbiased reflection of what the population is actually like. For instance, you can evaluate the effectiveness by dividing your population on the basis of gender, education, profession, and so on. It depends on how much information is available about your population and the scope of your study. Not to mention how detailed you want your study to be.
You May Also Like
Statistics students must have heard a lot of times that inferential statistics is the heart of statistics. Well, that is true and reasonable. While descriptive statistics are easy to comprehend, inferential statistics are pretty complex and often have different interpretations.
A variable is an attribute to which different values can be assigned. The value can be a characteristic, a number, or a quantity that can be counted. It is sometimes called a data item.
The standard normal distribution is a special kind of normal distribution where the mean is 0, and the standard deviation is 1.
USEFUL LINKS
LEARNING RESOURCES

COMPANY DETAILS

- How It Works
An overview of sampling methods
Last updated
27 February 2023
Reviewed by
Cathy Heath
When researching perceptions or attributes of a product, service, or people, you have two options:
Survey every person in your chosen group (the target market, or population), collate your responses, and reach your conclusions.
Select a smaller group from within your target market and use their answers to represent everyone. This option is sampling .
Sampling saves you time and money. When you use the sampling method, the whole population being studied is called the sampling frame .
The sample you choose should represent your target market, or the sampling frame, well enough to do one of the following:
Generalize your findings across the sampling frame and use them as though you had surveyed everyone
Use the findings to decide on your next step, which might involve more in-depth sampling
Make research less tedious
Dovetail streamlines research to help you uncover and share actionable insights
How was sampling developed?
Valery Glivenko and Francesco Cantelli, two mathematicians studying probability theory in the early 1900s, devised the sampling method. Their research showed that a properly chosen sample of people would reflect the larger group’s status, opinions, decisions, and decision-making steps.
They proved you don't need to survey the entire target market, thereby saving the rest of us a lot of time and money.
- Why is sampling important?
We’ve already touched on the fact that sampling saves you time and money. When you get reliable results quickly, you can act on them sooner. And the money you save can pay for something else.
It’s often easier to survey a sample than a whole population. Sample inferences can be more reliable than those you get from a very large group because you can choose your samples carefully and scientifically.
Sampling is also useful because it is often impossible to survey the entire population. You probably have no choice but to collect only a sample in the first place.
Because you’re working with fewer people, you can collect richer data, which makes your research more accurate. You can:
Ask more questions
Go into more detail
Seek opinions instead of just collecting facts
Observe user behaviors
Double-check your findings if you need to
In short, sampling works! Let's take a look at the most common sampling methods.
- Types of sampling methods
There are two main sampling methods: probability sampling and non-probability sampling. These can be further refined, which we'll cover shortly. You can then decide which approach best suits your research project.
Probability sampling method
Probability sampling is used in quantitative research , so it provides data on the survey topic in terms of numbers. Probability relates to mathematics, hence the name ‘quantitative research’. Subjects are asked questions like:
How many boxes of candy do you buy at one time?
How often do you shop for candy?
How much would you pay for a box of candy?
This method is also called random sampling because everyone in the target market has an equal chance of being chosen for the survey. It is designed to reduce sampling error for the most important variables. You should, therefore, get results that fairly reflect the larger population.
Non-probability sampling method
In this method, not everyone has an equal chance of being part of the sample. It's usually easier (and cheaper) to select people for the sample group. You choose people who are more likely to be involved in or know more about the topic you’re researching.
Non-probability sampling is used for qualitative research. Qualitative data is generated by questions like:
Where do you usually shop for candy (supermarket, gas station, etc.?)
Which candy brand do you usually buy?
Why do you like that brand?
- Probability sampling methods
Here are five ways of doing probability sampling:
Simple random sampling (basic probability sampling)
Systematic sampling
Stratified sampling.
Cluster sampling
Multi-stage sampling
Simple random sampling.
There are three basic steps to simple random sampling:
Choose your sampling frame.
Decide on your sample size. Make sure it is large enough to give you reliable data.
Randomly choose your sample participants.
You could put all their names in a hat, shake the hat to mix the names, and pull out however many names you want in your sample (without looking!)
You could be more scientific by giving each participant a number and then using a random number generator program to choose the numbers.
Instead of choosing names or numbers, you decide beforehand on a selection method. For example, collect all the names in your sampling frame and start at, for example, the fifth person on the list, then choose every fourth name or every tenth name. Alternatively, you could choose everyone whose last name begins with randomly-selected initials, such as A, G, or W.
Choose your system of selecting names, and away you go.
This is a more sophisticated way to choose your sample. You break the sampling frame down into important subgroups or strata . Then, decide how many you want in your sample, and choose an equal number (or a proportionate number) from each subgroup.
For example, you want to survey how many people in a geographic area buy candy, so you compile a list of everyone in that area. You then break that list down into, for example, males and females, then into pre-teens, teenagers, young adults, senior citizens, etc. who are male or female.
So, if there are 1,000 young male adults and 2,000 young female adults in the whole sampling frame, you may want to choose 100 males and 200 females to keep the proportions balanced. You then choose the individual survey participants through the systematic sampling method.
Clustered sampling
This method is used when you want to subdivide a sample into smaller groups or clusters that are geographically or organizationally related.
Let’s say you’re doing quantitative research into candy sales. You could choose your sample participants from urban, suburban, or rural populations. This would give you three geographic clusters from which to select your participants.
This is a more refined way of doing cluster sampling. Let’s say you have your urban cluster, which is your primary sampling unit. You can subdivide this into a secondary sampling unit, say, participants who typically buy their candy in supermarkets. You could then further subdivide this group into your ultimate sampling unit. Finally, you select the actual survey participants from this unit.
- Uses of probability sampling
Probability sampling has three main advantages:
It helps minimizes the likelihood of sampling bias. How you choose your sample determines the quality of your results. Probability sampling gives you an unbiased, randomly selected sample of your target market.
It allows you to create representative samples and subgroups within a sample out of a large or diverse target market.
It lets you use sophisticated statistical methods to select as close to perfect samples as possible.
- Non-probability sampling methods
To recap, with non-probability sampling, you choose people for your sample in a non-random way, so not everyone in your sampling frame has an equal chance of being chosen. Your research findings, therefore, may not be as representative overall as probability sampling, but you may not want them to be.
Sampling bias is not a concern if all potential survey participants share similar traits. For example, you may want to specifically focus on young male adults who spend more than others on candy. In addition, it is usually a cheaper and quicker method because you don't have to work out a complex selection system that represents the entire population in that community.
Researchers do need to be mindful of carefully considering the strengths and limitations of each method before selecting a sampling technique.
Non-probability sampling is best for exploratory research , such as at the beginning of a research project.
There are five main types of non-probability sampling methods:
Convenience sampling
Purposive sampling, voluntary response sampling, snowball sampling, quota sampling.
The strategy of convenience sampling is to choose your sample quickly and efficiently, using the least effort, usually to save money.
Let's say you want to survey the opinions of 100 millennials about a particular topic. You could send out a questionnaire over the social media platforms millennials use. Ask respondents to confirm their birth year at the top of their response sheet and, when you have your 100 responses, begin your analysis. Or you could visit restaurants and bars where millennials spend their evenings and sign people up.
A drawback of convenience sampling is that it may not yield results that apply to a broader population.
This method relies on your judgment to choose the most likely sample to deliver the most useful results. You must know enough about the survey goals and the sampling frame to choose the most appropriate sample respondents.
Your knowledge and experience save you time because you know your ideal sample candidates, so you should get high-quality results.
This method is similar to convenience sampling, but it is based on potential sample members volunteering rather than you looking for people.
You make it known you want to do a survey on a particular topic for a particular reason and wait until enough people volunteer. Then you give them the questionnaire or arrange interviews to ask your questions directly.
Snowball sampling involves asking selected participants to refer others who may qualify for the survey. This method is best used when there is no sampling frame available. It is also useful when the researcher doesn’t know much about the target population.
Let's say you want to research a niche topic that involves people who may be difficult to locate. For our candy example, this could be young males who buy a lot of candy, go rock climbing during the day, and watch adventure movies at night. You ask each participant to name others they know who do the same things, so you can contact them. As you make contact with more people, your sample 'snowballs' until you have all the names you need.
This sampling method involves collecting the specific number of units (quotas) from your predetermined subpopulations. Quota sampling is a way of ensuring that your sample accurately represents the sampling frame.
- Uses of non-probability sampling
You can use non-probability sampling when you:
Want to do a quick test to see if a more detailed and sophisticated survey may be worthwhile
Want to explore an idea to see if it 'has legs'
Launch a pilot study
Do some initial qualitative research
Have little time or money available (half a loaf is better than no bread at all)
Want to see if the initial results will help you justify a longer, more detailed, and more expensive research project
- The main types of sampling bias, and how to avoid them
Sampling bias can fog or limit your research results. This will have an impact when you generalize your results across the whole target market. The two main causes of sampling bias are faulty research design and poor data collection or recording. They can affect probability and non-probability sampling.
Faulty research
If a surveyor chooses participants inappropriately, the results will not reflect the population as a whole.
A famous example is the 1948 presidential race. A telephone survey was conducted to see which candidate had more support. The problem with the research design was that, in 1948, most people with telephones were wealthy, and their opinions were very different from voters as a whole. The research implied Dewey would win, but it was Truman who became president.
Poor data collection or recording
This problem speaks for itself. The survey may be well structured, the sample groups appropriate, the questions clear and easy to understand, and the cluster sizes appropriate. But if surveyors check the wrong boxes when they get an answer or if the entire subgroup results are lost, the survey results will be biased.
How do you minimize bias in sampling?
To get results you can rely on, you must:
Know enough about your target market
Choose one or more sample surveys to cover the whole target market properly
Choose enough people in each sample so your results mirror your target market
Have content validity . This means the content of your questions must be direct and efficiently worded. If it isn’t, the viability of your survey could be questioned. That would also be a waste of time and money, so make the wording of your questions your top focus.
If using probability sampling, make sure your sampling frame includes everyone it should and that your random sampling selection process includes the right proportion of the subgroups
If using non-probability sampling, focus on fairness, equality, and completeness in identifying your samples and subgroups. Then balance those criteria against simple convenience or other relevant factors.
What are the five types of sampling bias?
Self-selection bias. If you mass-mail questionnaires to everyone in the sample, you’re more likely to get results from people with extrovert or activist personalities and not from introverts or pragmatists. So if your convenience sampling focuses on getting your quota responses quickly, it may be skewed.
Non-response bias. Unhappy customers, stressed-out employees, or other sub-groups may not want to cooperate or they may pull out early.
Undercoverage bias. If your survey is done, say, via email or social media platforms, it will miss people without internet access, such as those living in rural areas, the elderly, or lower-income groups.
Survivorship bias. Unsuccessful people are less likely to take part. Another example may be a researcher excluding results that don’t support the overall goal. If the CEO wants to tell the shareholders about a successful product or project at the AGM, some less positive survey results may go “missing” (to take an extreme example.) The result is that your data will reflect an overly optimistic representation of the truth.
Pre-screening bias. If the researcher, whose experience and knowledge are being used to pre-select respondents in a judgmental sampling, focuses more on convenience than judgment, the results may be compromised.
How do you minimize sampling bias?
Focus on the bullet points in the next section and:
Make survey questionnaires as direct, easy, short, and available as possible, so participants are more likely to complete them accurately and send them back
Follow up with the people who have been selected but have not returned their responses
Ignore any pressure that may produce bias
- How do you decide on the type of sampling to use?
Use the ideas you've gleaned from this article to give yourself a platform, then choose the best method to meet your goals while staying within your time and cost limits.
If it isn't obvious which method you should choose, use this strategy:
Clarify your research goals
Clarify how accurate your research results must be to reach your goals
Evaluate your goals against time and budget
List the two or three most obvious sampling methods that will work for you
Confirm the availability of your resources (researchers, computer time, etc.)
Compare each of the possible methods with your goals, accuracy, precision, resource, time, and cost constraints
Make your decision
- The takeaway
Effective market research is the basis of successful marketing, advertising, and future productivity. By selecting the most appropriate sampling methods, you will collect the most useful market data and make the most effective decisions.
Should you be using a customer insights hub?
Do you want to discover previous research faster?
Do you share your research findings with others?
Do you analyze research data?
Start for free today, add your research, and get to key insights faster
Editor’s picks
Last updated: 18 April 2023
Last updated: 27 February 2023
Last updated: 6 February 2023
Last updated: 6 October 2023
Last updated: 5 February 2023
Last updated: 16 April 2023
Last updated: 9 March 2023
Last updated: 12 December 2023
Last updated: 11 March 2024
Last updated: 4 July 2024
Last updated: 6 March 2024
Last updated: 5 March 2024
Last updated: 13 May 2024
Latest articles
Related topics, .css-je19u9{-webkit-align-items:flex-end;-webkit-box-align:flex-end;-ms-flex-align:flex-end;align-items:flex-end;display:-webkit-box;display:-webkit-flex;display:-ms-flexbox;display:flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;-webkit-box-flex-wrap:wrap;-webkit-flex-wrap:wrap;-ms-flex-wrap:wrap;flex-wrap:wrap;-webkit-box-pack:center;-ms-flex-pack:center;-webkit-justify-content:center;justify-content:center;row-gap:0;text-align:center;max-width:671px;}@media (max-width: 1079px){.css-je19u9{max-width:400px;}.css-je19u9>span{white-space:pre;}}@media (max-width: 799px){.css-je19u9{max-width:400px;}.css-je19u9>span{white-space:pre;}} decide what to .css-1kiodld{max-height:56px;display:-webkit-box;display:-webkit-flex;display:-ms-flexbox;display:flex;-webkit-align-items:center;-webkit-box-align:center;-ms-flex-align:center;align-items:center;}@media (max-width: 1079px){.css-1kiodld{display:none;}} build next, decide what to build next.

Users report unexpectedly high data usage, especially during streaming sessions.

Users find it hard to navigate from the home page to relevant playlists in the app.

It would be great to have a sleep timer feature, especially for bedtime listening.

I need better filters to find the songs or artists I’m looking for.
Log in or sign up
Get started for free
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
Methodology
- What Is a Research Design | Types, Guide & Examples
What Is a Research Design | Types, Guide & Examples
Published on June 7, 2021 by Shona McCombes . Revised on November 20, 2023 by Pritha Bhandari.
A research design is a strategy for answering your research question using empirical data. Creating a research design means making decisions about:
- Your overall research objectives and approach
- Whether you’ll rely on primary research or secondary research
- Your sampling methods or criteria for selecting subjects
- Your data collection methods
- The procedures you’ll follow to collect data
- Your data analysis methods
A well-planned research design helps ensure that your methods match your research objectives and that you use the right kind of analysis for your data.
Table of contents
Step 1: consider your aims and approach, step 2: choose a type of research design, step 3: identify your population and sampling method, step 4: choose your data collection methods, step 5: plan your data collection procedures, step 6: decide on your data analysis strategies, other interesting articles, frequently asked questions about research design.
- Introduction
Before you can start designing your research, you should already have a clear idea of the research question you want to investigate.
There are many different ways you could go about answering this question. Your research design choices should be driven by your aims and priorities—start by thinking carefully about what you want to achieve.
The first choice you need to make is whether you’ll take a qualitative or quantitative approach.
| Qualitative approach | Quantitative approach |
|---|---|
| and describe frequencies, averages, and correlations about relationships between variables |
Qualitative research designs tend to be more flexible and inductive , allowing you to adjust your approach based on what you find throughout the research process.
Quantitative research designs tend to be more fixed and deductive , with variables and hypotheses clearly defined in advance of data collection.
It’s also possible to use a mixed-methods design that integrates aspects of both approaches. By combining qualitative and quantitative insights, you can gain a more complete picture of the problem you’re studying and strengthen the credibility of your conclusions.
Practical and ethical considerations when designing research
As well as scientific considerations, you need to think practically when designing your research. If your research involves people or animals, you also need to consider research ethics .
- How much time do you have to collect data and write up the research?
- Will you be able to gain access to the data you need (e.g., by travelling to a specific location or contacting specific people)?
- Do you have the necessary research skills (e.g., statistical analysis or interview techniques)?
- Will you need ethical approval ?
At each stage of the research design process, make sure that your choices are practically feasible.
Here's why students love Scribbr's proofreading services
Discover proofreading & editing
Within both qualitative and quantitative approaches, there are several types of research design to choose from. Each type provides a framework for the overall shape of your research.
Types of quantitative research designs
Quantitative designs can be split into four main types.
- Experimental and quasi-experimental designs allow you to test cause-and-effect relationships
- Descriptive and correlational designs allow you to measure variables and describe relationships between them.
| Type of design | Purpose and characteristics |
|---|---|
| Experimental | relationships effect on a |
| Quasi-experimental | ) |
| Correlational | |
| Descriptive |
With descriptive and correlational designs, you can get a clear picture of characteristics, trends and relationships as they exist in the real world. However, you can’t draw conclusions about cause and effect (because correlation doesn’t imply causation ).
Experiments are the strongest way to test cause-and-effect relationships without the risk of other variables influencing the results. However, their controlled conditions may not always reflect how things work in the real world. They’re often also more difficult and expensive to implement.
Types of qualitative research designs
Qualitative designs are less strictly defined. This approach is about gaining a rich, detailed understanding of a specific context or phenomenon, and you can often be more creative and flexible in designing your research.
The table below shows some common types of qualitative design. They often have similar approaches in terms of data collection, but focus on different aspects when analyzing the data.
| Type of design | Purpose and characteristics |
|---|---|
| Grounded theory | |
| Phenomenology |
Your research design should clearly define who or what your research will focus on, and how you’ll go about choosing your participants or subjects.
In research, a population is the entire group that you want to draw conclusions about, while a sample is the smaller group of individuals you’ll actually collect data from.
Defining the population
A population can be made up of anything you want to study—plants, animals, organizations, texts, countries, etc. In the social sciences, it most often refers to a group of people.
For example, will you focus on people from a specific demographic, region or background? Are you interested in people with a certain job or medical condition, or users of a particular product?
The more precisely you define your population, the easier it will be to gather a representative sample.
- Sampling methods
Even with a narrowly defined population, it’s rarely possible to collect data from every individual. Instead, you’ll collect data from a sample.
To select a sample, there are two main approaches: probability sampling and non-probability sampling . The sampling method you use affects how confidently you can generalize your results to the population as a whole.
| Probability sampling | Non-probability sampling |
|---|---|
Probability sampling is the most statistically valid option, but it’s often difficult to achieve unless you’re dealing with a very small and accessible population.
For practical reasons, many studies use non-probability sampling, but it’s important to be aware of the limitations and carefully consider potential biases. You should always make an effort to gather a sample that’s as representative as possible of the population.
Case selection in qualitative research
In some types of qualitative designs, sampling may not be relevant.
For example, in an ethnography or a case study , your aim is to deeply understand a specific context, not to generalize to a population. Instead of sampling, you may simply aim to collect as much data as possible about the context you are studying.
In these types of design, you still have to carefully consider your choice of case or community. You should have a clear rationale for why this particular case is suitable for answering your research question .
For example, you might choose a case study that reveals an unusual or neglected aspect of your research problem, or you might choose several very similar or very different cases in order to compare them.
Data collection methods are ways of directly measuring variables and gathering information. They allow you to gain first-hand knowledge and original insights into your research problem.
You can choose just one data collection method, or use several methods in the same study.
Survey methods
Surveys allow you to collect data about opinions, behaviors, experiences, and characteristics by asking people directly. There are two main survey methods to choose from: questionnaires and interviews .
| Questionnaires | Interviews |
|---|---|
| ) |
Observation methods
Observational studies allow you to collect data unobtrusively, observing characteristics, behaviors or social interactions without relying on self-reporting.
Observations may be conducted in real time, taking notes as you observe, or you might make audiovisual recordings for later analysis. They can be qualitative or quantitative.
| Quantitative observation | |
|---|---|
Other methods of data collection
There are many other ways you might collect data depending on your field and topic.
| Field | Examples of data collection methods |
|---|---|
| Media & communication | Collecting a sample of texts (e.g., speeches, articles, or social media posts) for data on cultural norms and narratives |
| Psychology | Using technologies like neuroimaging, eye-tracking, or computer-based tasks to collect data on things like attention, emotional response, or reaction time |
| Education | Using tests or assignments to collect data on knowledge and skills |
| Physical sciences | Using scientific instruments to collect data on things like weight, blood pressure, or chemical composition |
If you’re not sure which methods will work best for your research design, try reading some papers in your field to see what kinds of data collection methods they used.
Secondary data
If you don’t have the time or resources to collect data from the population you’re interested in, you can also choose to use secondary data that other researchers already collected—for example, datasets from government surveys or previous studies on your topic.
With this raw data, you can do your own analysis to answer new research questions that weren’t addressed by the original study.
Using secondary data can expand the scope of your research, as you may be able to access much larger and more varied samples than you could collect yourself.
However, it also means you don’t have any control over which variables to measure or how to measure them, so the conclusions you can draw may be limited.
Receive feedback on language, structure, and formatting
Professional editors proofread and edit your paper by focusing on:
- Academic style
- Vague sentences
- Style consistency
See an example

As well as deciding on your methods, you need to plan exactly how you’ll use these methods to collect data that’s consistent, accurate, and unbiased.
Planning systematic procedures is especially important in quantitative research, where you need to precisely define your variables and ensure your measurements are high in reliability and validity.
Operationalization
Some variables, like height or age, are easily measured. But often you’ll be dealing with more abstract concepts, like satisfaction, anxiety, or competence. Operationalization means turning these fuzzy ideas into measurable indicators.
If you’re using observations , which events or actions will you count?
If you’re using surveys , which questions will you ask and what range of responses will be offered?
You may also choose to use or adapt existing materials designed to measure the concept you’re interested in—for example, questionnaires or inventories whose reliability and validity has already been established.
Reliability and validity
Reliability means your results can be consistently reproduced, while validity means that you’re actually measuring the concept you’re interested in.
| Reliability | Validity |
|---|---|
| ) ) |
For valid and reliable results, your measurement materials should be thoroughly researched and carefully designed. Plan your procedures to make sure you carry out the same steps in the same way for each participant.
If you’re developing a new questionnaire or other instrument to measure a specific concept, running a pilot study allows you to check its validity and reliability in advance.
Sampling procedures
As well as choosing an appropriate sampling method , you need a concrete plan for how you’ll actually contact and recruit your selected sample.
That means making decisions about things like:
- How many participants do you need for an adequate sample size?
- What inclusion and exclusion criteria will you use to identify eligible participants?
- How will you contact your sample—by mail, online, by phone, or in person?
If you’re using a probability sampling method , it’s important that everyone who is randomly selected actually participates in the study. How will you ensure a high response rate?
If you’re using a non-probability method , how will you avoid research bias and ensure a representative sample?
Data management
It’s also important to create a data management plan for organizing and storing your data.
Will you need to transcribe interviews or perform data entry for observations? You should anonymize and safeguard any sensitive data, and make sure it’s backed up regularly.
Keeping your data well-organized will save time when it comes to analyzing it. It can also help other researchers validate and add to your findings (high replicability ).
On its own, raw data can’t answer your research question. The last step of designing your research is planning how you’ll analyze the data.
Quantitative data analysis
In quantitative research, you’ll most likely use some form of statistical analysis . With statistics, you can summarize your sample data, make estimates, and test hypotheses.
Using descriptive statistics , you can summarize your sample data in terms of:
- The distribution of the data (e.g., the frequency of each score on a test)
- The central tendency of the data (e.g., the mean to describe the average score)
- The variability of the data (e.g., the standard deviation to describe how spread out the scores are)
The specific calculations you can do depend on the level of measurement of your variables.
Using inferential statistics , you can:
- Make estimates about the population based on your sample data.
- Test hypotheses about a relationship between variables.
Regression and correlation tests look for associations between two or more variables, while comparison tests (such as t tests and ANOVAs ) look for differences in the outcomes of different groups.
Your choice of statistical test depends on various aspects of your research design, including the types of variables you’re dealing with and the distribution of your data.
Qualitative data analysis
In qualitative research, your data will usually be very dense with information and ideas. Instead of summing it up in numbers, you’ll need to comb through the data in detail, interpret its meanings, identify patterns, and extract the parts that are most relevant to your research question.
Two of the most common approaches to doing this are thematic analysis and discourse analysis .
| Approach | Characteristics |
|---|---|
| Thematic analysis | |
| Discourse analysis |
There are many other ways of analyzing qualitative data depending on the aims of your research. To get a sense of potential approaches, try reading some qualitative research papers in your field.
If you want to know more about the research process , methodology , research bias , or statistics , make sure to check out some of our other articles with explanations and examples.
- Simple random sampling
- Stratified sampling
- Cluster sampling
- Likert scales
- Reproducibility
Statistics
- Null hypothesis
- Statistical power
- Probability distribution
- Effect size
- Poisson distribution
Research bias
- Optimism bias
- Cognitive bias
- Implicit bias
- Hawthorne effect
- Anchoring bias
- Explicit bias
A research design is a strategy for answering your research question . It defines your overall approach and determines how you will collect and analyze data.
A well-planned research design helps ensure that your methods match your research aims, that you collect high-quality data, and that you use the right kind of analysis to answer your questions, utilizing credible sources . This allows you to draw valid , trustworthy conclusions.
Quantitative research designs can be divided into two main categories:
- Correlational and descriptive designs are used to investigate characteristics, averages, trends, and associations between variables.
- Experimental and quasi-experimental designs are used to test causal relationships .
Qualitative research designs tend to be more flexible. Common types of qualitative design include case study , ethnography , and grounded theory designs.
The priorities of a research design can vary depending on the field, but you usually have to specify:
- Your research questions and/or hypotheses
- Your overall approach (e.g., qualitative or quantitative )
- The type of design you’re using (e.g., a survey , experiment , or case study )
- Your data collection methods (e.g., questionnaires , observations)
- Your data collection procedures (e.g., operationalization , timing and data management)
- Your data analysis methods (e.g., statistical tests or thematic analysis )
A sample is a subset of individuals from a larger population . Sampling means selecting the group that you will actually collect data from in your research. For example, if you are researching the opinions of students in your university, you could survey a sample of 100 students.
In statistics, sampling allows you to test a hypothesis about the characteristics of a population.
Operationalization means turning abstract conceptual ideas into measurable observations.
For example, the concept of social anxiety isn’t directly observable, but it can be operationally defined in terms of self-rating scores, behavioral avoidance of crowded places, or physical anxiety symptoms in social situations.
Before collecting data , it’s important to consider how you will operationalize the variables that you want to measure.
A research project is an academic, scientific, or professional undertaking to answer a research question . Research projects can take many forms, such as qualitative or quantitative , descriptive , longitudinal , experimental , or correlational . What kind of research approach you choose will depend on your topic.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
McCombes, S. (2023, November 20). What Is a Research Design | Types, Guide & Examples. Scribbr. Retrieved July 10, 2024, from https://www.scribbr.com/methodology/research-design/
Is this article helpful?
Shona McCombes
Other students also liked, guide to experimental design | overview, steps, & examples, how to write a research proposal | examples & templates, ethical considerations in research | types & examples, "i thought ai proofreading was useless but..".
I've been using Scribbr for years now and I know it's a service that won't disappoint. It does a good job spotting mistakes”

In order to continue enjoying our site, we ask that you confirm your identity as a human. Thank you very much for your cooperation.
In a research proposal, which of the following sections discusses the types of scales to be used for data collection? a) Definition of the target population b) Sample design c) Data collection method d) Specific research instruments e) Definition of the sample size
The correct answer is option C. In a research proposal, the Data Collection method discusses the types of scales to be used for data collection.
The Data Collection Method section of a research proposal is where the various scales for data collection are discussed. The types of scales (such as Likert scales, qualitative scales , etc.) and specific research instruments (such as surveys, interviews, questionnaires, or focus groups) typically are described in this section. that will be applied to the measurement of the variables. The target population and the definition of the sample size might also be discussed in the sample design section.
Learn more about Data collection method :
https://brainly.com/question/30156823
Related Questions
15. a) Graph the following equation: 2x−y=−8
The graph of the function is added as an attachment
From the question, we have the following parameters that can be used in our computation:
Make y the subject
The above equation is a linear equation
A linear equation is represented as
y-intercept = c
This means that the slope is 2 and the y-intercept is 8
Next, we plot the graph of the equation
See attachment for the graph
Read more about linear equation at
brainly.com/question/2030026
The function g(x)=5x+3−−−−√3−5 is a transformation of the cube root parent function. How can these transformations be described? Drag words to the boxes to correctly complete the statement. Put responses in the correct input to answer the question. Select a response, navigate to the desired input and insert the response. Responses can be selected and inserted using the space bar, enter key, left mouse button or touchpad. Responses can also be moved by dragging with a mouse. The function g(x) is translated 3 units ___ Response area, 5 units___ Response area , and undergoes a vertical ___ Response area compared to its cube root parent function. left right up down stretch compression
The complete statement is,
The function g(x) is 3 units stretch Response area , and undergoes a vertical translated 5 unit right Response area compared to its cube root parent function.
Reflection is a type of transformation that flip a shape in mirror line, so that each point is the same distance from the mirror line as its reflected point.
We have to given that;
The function is,
⇒ f (x) = ∛(5x+ 3) - 5
This is a transformation of the cube root parent function.
Now, The parent function is,
⇒ f (x) = ∛x
After 5 units stretch Response area, we get;
⇒ g (x) = ∛5x
And, After translated 3 units right Response area,
⇒ g (x) = ∛ (5x + 3)
And, After translated 5 unit down, we get;
Thus, The complete statement is,
The function g(x) is 3 units stretch Response area , and undergoes a vertical translated 5 unit down Response area compared to its cube root parent function.
Learn more about the reflection visit:
https://brainly.com/question/26494295
3. Why is it useful to know the unit rate price of an item at a supermarket?
Answer: Looking at the unit price allows you to compare the price of different sized packages and different brands to find the best deal.
Step-by-step explanation: The "unit price" tells you the cost per pound, quart, or other unit of weight or volume of a food package. It is usually posted on the shelf below the food.
The unit rate price of an item at a supermarket is necessary to help buyers to understand and compare the prices for different things at the rate.
Shopkeepers sell their items according to some fixed unit rates. These rates can be used by the customer to compare within different qualities of that specific product and to understand how much quantity of goods they can purchase under their budget.
Everyone can easily learn about the amount of money to be paid to the shopkeeper. If we have unit rates we can compare the prices of items fairly in the market. So it is helpful to buy and sell the items at unit rates for a better economy .
Learn more about buyers,
https://brainly.com/question/21329957
Heritage Company uses a job-order costing system to assign costs to jobs. It had no work in process or finished goods inventories on hand at the beginning of May. The table below provides data concerning the only three jobs worked on in May. Job X Job Y Job Z Direct labor hours 200 80 120 Direct materials $ 4,800 $ 1,800 $ 3,600 Direct labor $ 2,400 $ 1,000 $ 1,500 Jobs X and Y were completed in May; however, only 150 of the 200 units included in Job X were sold in May, whereas all 100 of Job Y’s units were sold in May. Job Z was not completed by the end of the month. Overhead costs are applied to jobs based on direct labor-hours and the predetermined overhead rate is $45 per direct labor-hour. The company’s total applied overhead always equals its total actual overhead. Required: Compute the amount of overhead cost that would have been applied to each job during May. Compute the work in process inventory that would be reported in the company’s May 31 balance sheet. Compute the finished goods inventory that would be reported in the company’s May 31 balance sheet. Compute the cost of goods sold that would be reported in the company’s income statement for May.
a) The amount of overhead cost that would have been applied to each job during May, based on the predetermined overhead rate , was as follows:
Job X Job Y Job Z
Overhead applied $9,000 $3,600 $5,400
b) The work-in-process inventory reported in the company's May 31 balance sheet was $10,500 for Job Z only.
c) The finished goods inventory that would be reported in the company’s May 31 balance sheet was $4,050.
d) The cost of goods sold that would be reported in the company's income statement for May was $14,500.
The predetermined overhead rate is the rate per unit at which overhead costs are applied to production units or jobs.
The predetermined overhead rate is the quotient of the total budgeted overhead cost divided by the relevant total cost driver units (e.g. direct labor hours).
Predetermined overhead rate = $45 per direct labor-hour
Direct labor hours 200 80 120
Direct materials $4,800 $1,800 $3,600
Direct labor 2,400 1,000 1,500
Overhead applied 9,000 3,600 5,400
($45 x 200) ($45 x 80) ($45 x 120)
Production costs $16,200 $6,400 $10,500
Unit costs of Job X $81 ($16,200/200)
Sold units of Job X = 150
Unsold units of Job X = 50 (200 - 150)
Work in process inventory = Job Z's total cost.
Finished Goods Inventory = $4,050 ($81 x 50)
Cost of Goods Sold = $14,500 ($6,400 + $81 x 100)
Learn more about the predetermined overhead rate at https://brainly.com/question/4337723
from a set of 52 poker cards (without 2 jokers), we keep taking cards randomly one by one with replacement, until all the cards taken by us can cover all 4 shades. (1) compute the probability that we have picked exactly n cards. (2) verify that, after taking summation over n
1. To compute the probability that we have picked exactly n cards, we need to consider the number of ways to pick n cards out of 52 such that all 4 shades are represented, and divide that by the total number of possible n-card combinations from the deck of 52.
The number of ways to pick n cards such that all 4 shades are represented is given by the number of combinations of n items taken 4 at a time, with repetition allowed (denoted as C(n-1,3) or C(n+3-1,n)). This is because there are 4 shades , and we need to pick one card from each shade.
The total number of possible n- card combinations from the deck of 52 is given by C (52, n).
Therefore, the probability that we have picked exactly n cards is given by:
P(n) = C(n-1,3) / C(52, n)
2. To verify that the probability sums up to 1, we need to take the summation over all possible values of n, from n=4 to n=52:
P = sum(P(n)) from n=4 to n=52
If P is equal to 1, then the probability of picking exactly n cards over all possible values of n adds up to 1, which means that the event of picking all 4 shades is certain to occur at some point.
To know more about Probability :
https://brainly.com/question/30034780
HELP!!!Joe can type 40 words every 2 minutes. How many words can he type in 5 minutes?
Step-by-step explanation:
40+40 =80 +20=100
NO LINKS!!! Find the probability of randomly entering each room.
P(A) = 11/18
P(B) = 5/18
=====================================================
Explanation:
Check out the diagram below. I have marked your given diagram with fractions. The red fractions 1/3, 1/3, and 1/3 are probabilities that correspond to picking the left-most set of 3 branches. Each has 1/3 chance of randomly being selected. This assumes any of the branches are equally likely.
The blue fractions 1/2 and 1/3 are the probabilities for the next set of sub-branches. For instance, the upper pair of branches each have probability 1/2 of being randomly selected, since we have two of them.
The green fractions are the result of multiplying the red and blue fractions along a particular pathway. Eg: The upper-most pathway has (1/3)*(1/2) = 1/6
---------------
The diagram below shows that:
Side notes:
Jill has 2/5 of a cup of powdered sugar. She sprinkles 1/6 of the sugar onto a plate of brownies and sprinkles the rest onto a plate of lemon cookies. How much sugar does Jill sprinkle on the brownies?
The amount of sugar that Jill sprinkles on the brownies will be 1/15 cusp.
Algebra is the study of abstract symbols, while logic is the manipulation of all those ideas.
The acronym PEMDAS stands for Parenthesis, Exponent, Multiplication, Division, Addition, and Subtraction. This approach is used to answer the problem correctly and completely.
Jill has 2/5 of a cup of powdered sugar. She sprinkles 1/6 of the sugar onto a plate of brownies and sprinkles the rest onto a plate of lemon cookies.
Then the amount of sugar that Jill sprinkles on the brownies is given as,
⇒ (2/5) x (1/6)
More about the Algebra link is given below.
https://brainly.com/question/953809
Each letter of the alphabet is assigned an integer, starting with A = 0, B = 1, and so on. The numbers repeat after every seven letters, so that G = 6, H = 0, and I = 1, continuing on to Z. What two-letter word is represented by the digits 16? (MT calendar problem)
The two letter word represented by the digits 16 is given as follows:
Considering the pattern, the digits representing each letter are given as follows:
Hence the first letter can be:
B, I, P or X.
The second letter can be:
Hence the word is:
More can be learned about patterns at https://brainly.com/question/6561461
In this figure, h = 6, and r = 8. What is the exact surface area of the cone? Enter your answer in the box. units²
The surface area of Cone is 452.16 unit².
The surface area of a cone is equal to the curved surface area plus the area of the base : π r² + πlr
where r is the radius and l is the slant height .
Radius = 8 unit
height = 6 unit
slant height , l = √8²+6²= √64+36 =√100= 10units
So, the Surface area of Cone
= πr (l +r)
= 3.14 x 8 ( 10 + 8)
= 25.12 x 18
= 452.16 unit²
Learn more about Surface area of Cone here:
https://brainly.com/question/23877107
Simplify 9x^2 -4x-3= [?] x= -2
Simplify: [tex]9x^2 -4x-3=[/tex] [?] when x= -2
Substitute in -2 for x:
[tex]9(-2)^2 -4(-2)-3\\= 9(-2)^2 -4(-2)-3\\=9(4) +8 -3\\= 36 + 8 - 3\\[/tex]
Answer: = 41
One leg of a right triangle has a length of 7m. The other sides have lengths that are consecutive integers. Find the lengths
24 m, 25 m
You want the two sides of a right triangle that are consecutive integers when one side is 7 m .
Let the shorter side be represented by x. Then the longer side is x+1, and the Pythagorean theorem tells you ...
7² +x² = (x+1)²
49 +x² = x² +2x +1
48 = 2x . . . . . . subtract (x²+1)
The other sides are 24 and 25 meters .
Additional comment
You know that 7 is not the hypotenuse, because a 3-4-5 right triangle is the only right triangle with consecutive integer leg lengths and a hypotenuse of 7 or less. (The next nearest right triangle with consecutive leg lengths is {20, 21, 29}, with a hypotenuse of 29.)
You may recognize the side lengths as the Pythagorean Triple {7, 24, 25}, one of the triples commonly seen in algebra and trig problems.
After Game 6 of the 2016 NBA Finals, Frank put down an even-money $100,000 bet on the Cavs to win Game 7 (and therefore, the championship). So, if the Cavs win, he wins $100,000, and if the Cavs lose, he loses $100,000. Suppose Frank has a logarithmic utility-of-wealth function: U(w) = ln(w), and his current wealth is $1,000,000 (one million dollars). Given that he accepted this bet, what can we determine about p, the probability with which Frank believes the Cavs will win Game 7? The goal of this problem is to figure this out. The subparts below will walk you through figuring this out a) Write down an expression for Frank’s expected utility of wealth, as a function of p, if he takes the bet. [Remember to take into account his current wealth level as well as how winning or losing will change it.] b) Frank’s other option is to reject the bet. What will his utility of wealth be if he rejects the bet? c) If he accepts the bet, we know that the utility given for (a) must be larger than the utility given for (b). Write down and solve the inequality. You should be able to determine either a lower bound or upper bound for p, e.g. p ≤ 0.25 or p ≥.80. d) Suppose Frank’s utility-of-wealth function was less curved, i.e. closer to a straight line. How would the bound from (c) change? Remember, the bound defines the range of possible probabilities p for him to accept the bet. Explain why it would be larger or smaller.
Frank's expected utility of wealth function if he takes the bet is U(w) = $1,000,000 + p(ln($100,000)) + (1-p)(ln($900,000)). If Frank accepts the bet, the probability p must be greater than or equal to 0.8.
a) Frank's expected utility of wealth if he takes the bet is U(w) = $1,000,000 + p(ln($100,000)) + (1-p)(ln($900,000))
b) If Frank rejects the bet, his utility of wealth will be U(w) = ln($1,000,000)
c) U(w) = $1,000,000 + p(ln($100,000)) + (1-p)(ln($900,000)) ≥ ln($1,000,000)
p(ln($100,000)) + (1-p)(ln($900,000)) ≥ ln($1,000,000) - $1,000,000
p(ln($100,000)) + (1-p)(ln($900,000) - ln($1,000,000)) ≥ -$1,000,000
p(ln($100,000) - ln($1,000,000)) + (1-p)(ln($900,000) - ln($1,000,000)) ≥ -$1,000,000
p(ln($100,000/$1,000,000)) + (1-p)(ln($900,000/$1,000,000)) ≥ -$1,000,000
p(ln(0.1)) + (1-p)(ln(0.9)) ≥ -$1,000,000
p(ln(0.1)) ≥ -$1,000,000 - (1-p)(ln(0.9))
p ≥ (-$1,000,000 - (1-p)(ln(0.9)))/(ln(0.1))
p ≥ -$1,000,000/(ln(0.1)) - (1-p)(ln(0.9))/ln(0.1)
d) If Frank's utility of wealth function was less curved, i.e. closer to a straight line, the bound from (c) would be larger. This is because, with a less curved utility of wealth function , Frank would be less risk-averse and therefore more likely to accept the bet.
learn more about function here
https://brainly.com/question/12431044
Isaac is buying ingredients to bake 4 batches of chocolate chip walnut cookies, and each batch requires 1 bag each of chocolate chips and walnuts. His receipt shows a total of $17.92. He remembers that the chocolate chips were $2.59 per bag, but he can't remember how much each bag of walnuts costs. How can Isaac determine the cost per bag of walnuts? Match each step of the arithmetic solution with the correct description. Step 1 Step 2 :: Divide 17.92 by 4. II :: Subtract 2.59 from 4.48. :: Add 2.59 to 4.48. :: Multiply 17.92 by 4. :: Subtract 2.59 from 71.68.
The cost of each bag of walnut can be determined following the below steps and each bag of walnut is $1.89
Total receipt= $17.92
4 batches of chocolate chip walnut cookies requires 4 bags each of chocolate chips and walnuts if each batch requires 1 bag each of chocolate chips and walnuts
Cost of chocolate chips = $2.59
Cost of 4 bags of chocolate chips = 4($2.59)
Total cost of 4 bags of walnuts = Total receipt - Cost of 4 bags of chocolate chips
= $17.92 - $10.36
Cost of each bag of walnut= Total cost of 4 bags of walnuts / 4
= $7.56 / 4
Therefore, each bag of walnut cost $1.89
Read more on cost :
https://brainly.com/question/19104371
Answer: Step 1: Divide 17.92 by 4
Step 2: Subtract 2.59 from 4.48
Which transformations have been performed on the graph of f(x)=x√3 to obtain the graph of g(x)=2x−3−−−−√3+4? Select each correct answer. Responses reflect the graph over the x-axis reflect the graph over the x -axis translate the graph up translate the graph up translate the graph down translate the graph down translate the graph to the right translate the graph to the right stretch the graph away from the x-axis stretch the graph away from the x -axis translate the graph to the left translate the graph to the left compress the graph closer to the x-axis
The transformations have been performed on the graph of f(x)=x√3 to obtain the graph of g(x)=2x−3√3+4 are :
Graph is a representation of data in a table that is displayed in the form of an image. In addition, graphics can also be interpreted as a combination of data in the form of numbers, letters, symbols, pictures, words and paintings presented in the media to provide an overview of data from material representatives and material recipients. in the process of sending information .
Graphics are a combination of numbers, letters, symbols, pictures, words and paintings presented in the media to convey concepts or ideas from the sender to the target in providing information.
Learn more about graph at
https://brainly.com/question/16608196
The y-intercept of the estimated line of best fit is at (0,b). Enter the appropriate value of b. Enter the appropriate slope of the estimated line of best fit. please ♥️
Since the y-intercept of the estimated line of best fit is at (0, b), the appropriate value of b is 360.
The appropriate slope of the estimated line of best fit is -30
In Mathematics, the y-intercept is also referred to as an initial value and the y-intercept of any graph such as a linear function, generally occur at the point where the value of "x" is equal to zero (x = 0). Therefore, the y-intercept is at (0, 360).
In Mathematics, the slope of any straight line can be determined by using this mathematical equation;
Slope (m) = (Change in y-axis, Δy)/(Change in x-axis, Δx)
Slope (m) = (y₂ - y₁)/(x₂ - x₁)
Based on the information provided, we can logically deduce the following data points on the line:
Substituting the given points into the slope formula, we have the following;
Slope, m = (y₂ - y₁)/(x₂ - x₁)
Slope, m = (360 - 0)/(0 - 12)
Slope , m = -30.
Read more on slope here: brainly.com/question/3493733
the barge b is pulled by two tugboats a and c. at a given instant, the tension in cable ab is 4500 lb and the tension in cable bc is 2000 lb. determine by trigonometry the magnitude and direction of the resultant of the two forces applied at b at that instant.
To determine the magnitude and direction of the resultant force applied at b, we can use vector addition of the tensions in cables AB and BC. Let's assume that the positive x-direction is to the right, and the positive y-direction is upwards.
We can represent the tension in cable AB as a vector T1 = 4500 lb in the direction of AB, and the tension in cable BC as a vector T2 = 2000 lb in the direction of BC.
The magnitude of the resultant force applied at b is given by:
R = √(T1^2 + T2^2) = √(4500^2 + 2000^2) = 5000 lb
The direction of the resultant force can be found using the arctangent function:
θ = tan^-1 (T2/T1) = tan^-1 (2000/4500) = approximately 39.2 degrees
Therefore, the magnitude and direction of the resultant force applied at b are 5000 lb and 39.2 degrees, respectively.
To know more about Trigonometry
https://brainly.com/question/25618616
2 5 9 10 Which statements are true? Select the two correct answers. The square root of a positive number greater than 1 is less than the number. The square root of a positive number is always less than half of the number itself. The square root of a positive number less than 1 is less than the number. The square root of a perfect square is not a whole number. The square root of a positive number less than 1 is between 0 and 1. TIME REM 38:-
Find the median and mean of the data set below: 21 , 40 , 48 , 26 , 32 , 31
What does the problem asks for:
--> mean and median
Let's calculate the mean:
[tex]\text{Mean}=\dfrac{\text{sum of all the numbers}}{\text{number of numbers given}}[/tex]
--> the sum of all the numbers = 21 + 40 + 48 + 26+ 32 + 31 = 198
--> number of numbers given: 6
==> let's calculate
[tex]\text{Mean}=\dfrac{198}{6} =33[/tex]
Let's calculate the median
--> Median definition: middle number in an ordered sequence
==> let's order the sequence : 21, 26, 31, 32, 40, 48
--> since there are an even number of numbers, there isn't an exact
middle number
--> thus, we must find the mean of the two numbers closest to the
middle
[tex]\text{Median} = \dfrac{31+32}{2} =\dfrac{63}{2} =31.5[/tex]
Answer : 31.5
21, 26, 31, 32, 40, 48
3 1 + 3 2 = 6 3
6 3 ÷ 2 = 3 1 . 5
21+26+31+32+40+48=198
1 9 8 ÷ 6 = 3 3
true/false. an experiment was run to compare four groups. the standard deviations were 4974, 6585, 3288, 5488. in this case, it is reasonable to assume all groups have equal variances.
False . It is not reasonable to assume all groups have equal variances in this case.
The standard deviation is a measure of variability or spread of the data. If the standard deviations of different groups are significantly different, then it suggests that the spread of the data within each group is also different. When comparing multiple groups , equal variances are typically assumed so that a valid statistical test can be performed.
If the variances are unequal, then a different type of test, such as Welch's ANOVA , should be used. In this case, the large difference in the standard deviations of the four groups (4974, 6585, 3288, 5488) suggests that it is not reasonable to assume equal variances and a different test should be used.
Learn more about variances :
https://brainly.com/question/15858152
Graph the following system of equations. y = 3x + 9 6x − 2y = 6 What is the solution to the system? A There is no solution. B There is one unique solution (−1, −6). C There is one unique solution (0, −3). D There are infinitely many solutions.
The given system of simultaneous equations has no solutions .
In mathematics, a set of simultaneous equations , also known as a system of equations or an equation system, is a finite set of equations for which common solutions are sought.
Given is the system of simultaneous equations as -
6x − 2y = 6
Refer to the graph of the equations attached. The value of {x} and {y} for which both the equations are true is given by the point of intersection of both lines. Since both lines are parallel , there is no point of intersection and hence no solution .
Therefore, the given system of simultaneous equations has no solutions .
To solve more questions on simultaneous linear equations , visit the link below -
brainly.com/question/16763389
PLS HELP QUICK ITS IN THE PHOTO BTW Question 1 What is the total number of minutes spent reading? A 170 minutes B 195 minutes C 205 minutes D 220 minutes Question 2 What is the mode of the data set? 18, 23, 12, 21, 23 A 12 B 18 C 21 D 23 Question 3 What is the median of the data table? ITS IN THE PICTURE BTW A 20 B 25 C 30 D 35 Question 4 Select the data set with more than one mode. A 19, 23, 15, 23, 15 B 19, 40, 22, 26, 22 C 26, 23, 19, 25, 23 D 26, 34, 27, 29, 30 Question 5 Select the expression that shows how much more time was spent reading on Thursday than Saturday. ITS IN THE PICTURE BTW A 35 – 20 B 35 – 30 C 45 – 20 D 45 – 30 Question 6 Select the data set with no mode A 38, 17, 24, 25, 17 B 38, 34, 26, 29, 40 C 24, 17, 21, 17, 21 D 24, 30, 22, 24, 25 Question 7 What is the range of the data set? 28, 32, 22, 20, 25 A 12 B 25 C 32 D 48 Question 8 What is the median of the data set? LAST QUESTION 44, 32, 18, 25, 32 18 25 32 44
hope those are right
Dilate pint C using center D and scale factor 3/4
The dilations relation is C'D = (3/4)CD.
Dilation of a figure will leave its sides get scaled (multiplied) by same number. That number is called the scale factor of that dilation.
Its also called scaling of a figure, but due the involvement of coordinates, it involves a center of a dilation, which is like a pinned point which stays at same place after dilation.
Its like we enlarge or shorten the size of the figure (or keep it same, when scale factor = 1).
First, we want to dilate point C using D as the center of dilation with a scale factor = 3/4.
This only means that we will have the new point C', such that:
C'D = (3/4)*CD
Where CD is the distance between points C and D
Therefore, the dilation will be C'D = (3/4)*CD.
If you want to learn more about dilations , you can read;
brainly.com/question/3457976
give a geometric description of a system of 2 linear equations in 3 variables and its possible solution sets
The given of the system of equation is has No solution, parallel lines.
To give a geometric description of the given system of equations.
The geometric description of a system of equations in 2 variables mean the system of equations will represent the number of lines equal to the number of equations in the system given.
Number of planes = Number of variables
Number of lines = Number of equations in the system.
Here, we are given 2 variables and 2 equation in each system.
So, they can be represented in the xy-coordinates plane.
And the number of solutions to the system depends on the following condition.
Let the system of equations be:
A1x+B1y+C1=0
A2x+B2Y+C2=0
1. One solution:
There will be one solution to the system of equations, If we have:
[tex]\frac{A_1}{A_2} not\ equal to \ B_1/B_2[/tex]
2. Infinitely Many Solutions: (Identical lines in the system)
the ratio of A1 and A2 equal to ratio of B1 and B2 and equal toC1 and C2
3. No Solution:(Parallel lines)
the ratio of A1 and A2 equal to ratio of B1 and B2 but not equal ltoC1 and C2
Now, let us discuss the system of equations one by one:
a) A1=2, B1=-4 , C1=-12
A2=-3 , B2= 6 ,C2 = 15
Therefore, no solution i.e. parallel lines.
The complete question is-
Give a geometric description of the following system of equations.a. 2x−4y=12 −3x+6y=−15
learn more about system of equations.
https://brainly.com/question/12895249
Solve |x + 3 = -7. Please help
B. No solution
The output of an absolute value function can never be a negative number.
Absolute value is the distance between a number |x| and 0 and that distance will always be positive.
Answer: B: No solution
the following scatterplot shows the relationship between the left and right forearm lengths (cm) for 55 college students along with the regression line, left arm
The scatterplot shows a linear relationship between left and right forearm lengths in cm, for 55 college students.
The regression line is the best fit line that describes the relationship between the two variables. The formula for a linear regression line is y = mx + b, where m is the slope of the line and b is the y-intercept. The slope of the line in the scatterplot is 0.95, which indicates that for every 1 cm increase in the left arm, there is a 0.95 cm increase in the right arm . The y-intercept of the regression line is 8.4, meaning that when the left arm is 0, the right arm is 8.4 cm long. The equation for the regression line in the scatterplot is y = 0.95x + 8.4. This equation can be used to predict the right arm length for any given left arm length.
Learn more about regression line here:
https://brainly.com/question/7656407
Each truck from Jones Removal Company can haul 500 pound of trash at a time. On Wednesday, the company has jobs to remove 1,500 pounds of trash from one site, 500 from another site, and 2,500 from a third site. How many total pounds of trash will be moved by Jones Company that day? How many trips will it take for the Jones Company to remove all of the trash?
The total pounds of trash is 4500 pounds. Then the number of trips that will take for the Jones Company to remove all of the trash will be 9.
Each truck from Jones Expulsion Organization can pull 500 pounds of waste at a time. On Wednesday , the organization has tasks to eliminate 1,500 pounds of garbage from one site, 500 from another site , and 2,500 from a third site.
The total pounds of trash is given as,
⇒ 1500 + 500 + 2500
⇒ 4500 pounds
The number of trips will it take for the Jones Company to remove all of the trash will be given as,
⇒ 4500 / 500
A car owner pays for new brakes that cost $756.25, with a credit card that has an annual rate of 24.5%. Determine the total amount paid, if the car owner pays $100 a month, until the balance is paid off. A spreadsheet was used to calculate the correct answer. Your answer may vary slightly depending on the technology used. $830.52 $73.76 $892.64 $185.28
The rough calculation yields a amount of $900
If you carry a balance on your credit card, the card company will multiply it each day by a daily interest rate and add that to what you owe. The daily rate is your annual interest rate (the APR) divided by 365. For example, if your card has an APR of 16%, the daily rate would be 0.044%.
Given here: price of brakes =$756.25 and annual rate on credit card is 24.25%
Thus the if installment is $100 then It will take 9 months to payoff the balance. The total interest is $73.54.
Hence, The rough calculation yields a amount of $900
Learn more about installments here;
https://brainly.com/question/25845758
got it right on test..
The students in a club are selling flowerpots to raise money. Each flowerpot sells for $15. Part B The goal of the students in the club was to raise $500. They sold 43 flowerpots. By what amount did the students exceed their goal of raising $500? Show or explain all your work.
A cubic root function has a domain of x≥−3 and a range of y≥−1. What is the range of its inverse?
In general, if the range of a function is y≥−1, its inverse has a domain of y≥−1. So, the range of the inverse of the cubic root function is y≥−1.
The range of a cubic root function becomes the domain of a cube function and vice versa since a cubic root function is an inverse function of a cube function. Therefore, the cube function's range is x3 if the cubic root function's domain is x3.
A function's inverse typically has a domain of y1 if its range is y1. Therefore, y1 is the domain of the inverse of the cubic root function .
Describe a function.
A function is a mathematical relationship between a domain —a set of inputs—and a range—a set of outputs. Each input in the domain is given a distinct output, known as the function value, by a function. An equation or graph can be used to depict the function value .
A function is typically represented symbolically by an equation that describes the relationship between the inputs and outputs and a letter, like f or g, as well as the letter. For instance, the equation of a function that accepts a value of x as input and produces its square is f(x) = x2.
Learn more about Functions here
https://brainly.com/question/17043948

IMAGES
VIDEO
COMMENTS
A population is the entire group that you want to draw conclusions about. A sample is the specific group that you will collect data from. The size of the sample is always less than the total size of the population. In research, a population doesn't always refer to people. It can mean a group containing elements of anything you want to study ...
Discover the significance of research population and sample in statistical inference. Learn how sampling techniques shape accurate insights and informed decisions.
design, population of interest, study setting, recruit ment, and sampling. Study Design. The study design is the use of e vidence-based. procedures, protocols, and guidelines that provide the ...
Sampling methods are crucial for conducting reliable research. In this article, you will learn about the types, techniques and examples of sampling methods, and how to choose the best one for your study. Scribbr also offers free tools and guides for other aspects of academic writing, such as citation, bibliography, and fallacy.
1. Research Proposal Format Example. Following is a general outline of the material that should be included in your project proposal. I. Title Page II. Introduction and Literature Review (Chapters 2 and 3) A. Identification of specific problem area (e.g., what is it, why it is important). B. Prevalence, scope of problem.
Sampling refers to the process of defining a subgroup (sample) from the larger group of interest (population). The two overarching approaches to sampling are probability sampling (random) and non-probability sampling. Common probability-based sampling methods include simple random sampling, stratified random sampling, cluster sampling and ...
A population is a complete set of people with specified characteristics, while a sample is a subset of the population. 1 In general, most people think of the defining characteristic of a population in terms of geographic location. However, in research, other characteristics will define a population. Additional defining characteristics may be clinical, demographic, and temporal. For example ...
A research proposal aims to show why your project is worthwhile. It should explain the context, objectives, and methods of your research.
Step 2: Choose a type of research design. Step 3: Identify your population and sampling method. Step 4: Choose your data collection methods. Step 5: Plan your data collection procedures. Step 6: Decide on your data analysis strategies. Frequently asked questions. Introduction. Step 1. Step 2.
Research studies are usually carried out on sample of subjects rather than whole populations. The most challenging aspect of fieldwork is drawing a random sample from the target population to which the results of the study would be generalized. In actual ...
Probability sampling is a sampling technique in which every individual in the population has an equal chance of being selected as a subject for the research. There are several different types of probability samples you can use, depending on the resources you have available.
The essential topics related to the selection of participants for a health research are: 1) whether to work with samples or include the whole reference population in the study (census); 2) the sample basis; 3) the sampling process and 4) the potential effects nonrespondents might have on study results. We will refer to each of these aspects ...
This tutorial overviews the elements of a participants section for a quantitative research proposal.This video is part of A Guide for Developing a Quantitati...
Learn the difference between population and sample in research, the types and methods of sampling, and how to write this section in your paper.
In research, it's not always possible to collect data from an entire population group. Sampling is collecting data from a smaller group of people who participate in the research. Discover the types…
The purpose of this article is to present clear definitions of the population structures essential to research, to provide examples of how these structures are described within research, and to propose a basic structure that novice research-ers may use to ensure a clearly and completely defined population of interest and sample from which they will collect data.
Chapter 3 outlines the research design, the research method, the population under study, the sampling procedure, and the method that was used to collect data. The reliability and validity of the research instrument are addressed. Ethical considerations pertaining to the research are also discussed.
ABSTRACT This study highlights the fundamental concepts of population and sample in research and their crucial role in drawing valid conclusions. The population refers to the entire group or phenomenon being studied, while the sample is a subset used to represent it practically. The article stresses the importance of representativeness in sampling, where a well-chosen sample accurately ...
A research design is a strategy for answering your research question using empirical data. Creating a research design means making decisions about: Your overall research objectives and approach. Whether you'll rely on primary research or secondary research. Your sampling methods or criteria for selecting subjects. Your data collection methods.
Aim of the Chapter Data collection methods, research populations and samples and sampling methods are fundamental elements of the methodological framework, the third framework in the four frameworks approach to the research project.
Concept Paper and Proposals Future Tense Final Report Past Tense Participants Target population and the sample that you will use for generalizing about the target population. Demographic information such as age, gender, and ethnicity of your sample.
63 CHAPTER 3 METHODOLOGY The population and sample of this study are identified in Chapter 3. Methods of data collection, including the development and administration of a survey are discussed. Procedures used to interview a subset of the sample are described. Both descriptive and qualitative methods were combined in this research.
Learn about population and sample in research. Understand the role of a subset of a population in research, and see the differences between...
The correct answer is option C. In a research proposal, the Data Collection method discusses the types of scales to be used for data collection.. The Data Collection Method section of a research proposal is where the various scales for data collection are discussed.The types of scales (such as Likert scales, qualitative scales, etc.) and specific research instruments (such as surveys ...